Solved Problem on Static Equilibrium
advertisement
A block with mass m = 100 kg is suspended by the rope system shown in the figure. Determine the
tension forces on all ropes.
Assume: \( \sin 15°=0.259 \), \( \cos 15°=0.966 \), \( \sin 45°=0.707 \), \( \cos 45°=0.707 \), \( \sin 60°=0.866 \), \( \cos 60°=0.5 \).
Assume: \( \sin 15°=0.259 \), \( \cos 15°=0.966 \), \( \sin 45°=0.707 \), \( \cos 45°=0.707 \), \( \sin 60°=0.866 \), \( \cos 60°=0.5 \).

Problem data:
- Mass of the block: m=100 kg;
- Acceleration due to gravity: g=9.8 m/s2.
Drawing the forces acting on the system (Figure 1).
On the block, the gravitational force \( {\vec F}_{g} \) is balanced by the tension force \( {\vec T}_{1} \), which has a reaction force \( {\vec T}\text{'}_{1} \) on the ceiling, and by the tension force \( {\vec T}_{2} \), which has a reaction force \( {\vec T}\text{'}_{2} \) applied at point D.
At point D the tension force \( {\vec T}\text{'}_{2} \) is balanced by tension forces \( {\vec T}_{3} \) and \( {\vec T}_{4} \), which have as reaction forces \( {\vec T}\text{'}_{3} \) and \( {\vec T}\text{'}_{4} \) on the ceiling.
On the block, the gravitational force \( {\vec F}_{g} \) is balanced by the tension force \( {\vec T}_{1} \), which has a reaction force \( {\vec T}\text{'}_{1} \) on the ceiling, and by the tension force \( {\vec T}_{2} \), which has a reaction force \( {\vec T}\text{'}_{2} \) applied at point D.
At point D the tension force \( {\vec T}\text{'}_{2} \) is balanced by tension forces \( {\vec T}_{3} \) and \( {\vec T}_{4} \), which have as reaction forces \( {\vec T}\text{'}_{3} \) and \( {\vec T}\text{'}_{4} \) on the ceiling.
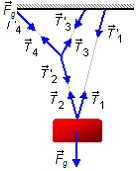
Figure 1
Solution:
Since the system is in equilibrium, the resultant forces are zero, and we apply the condition
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum F=0} \tag{I}
\end{gather}
\]
The problem is divided into two parts, first studying the forces on the block.
From point C, we draw a vertical line perpendicular to the ceiling, the angle between the ceiling and the rope \( \overline{CE} \) is 75°, so the angle between the line and the rope \( \overline{CE} \) is 15°, they are complementary angles, adding 90°.
From the block at point E, we draw a vertical line dividing the 30° angle into two parts. Since the angle between this line and rope \( \overline{CE} \) is an internal angle with the angle found before, it will also measure 15°. This line divides the 30° angle into two equal parts and is a bisector of the 30° angle (Figure 2-A).

Drawing the forces acting on the block in a xy coordinate system and decomposing the forces. The gravitational force \( {\vec F}_{g} \) has only the component \( {\vec F}_{gy} \), while the tension forces \( {\vec T}_{1} \) and \( {\vec T}_{2} \) have components \( {\vec T}_{1x} \) and \( {\vec T}_{2x} \) in the x direction, and components \( {\vec T}_{1y} \) and \( {\vec T}_{2y} \) in the y direction.
\[
\begin{gather}
{\vec T}_1+{\vec T}_2+\vec P=0 \\[5pt]
{\vec T}_{1x}+{\vec T}_{1y}-{\vec T}_{2x}+{\vec T}_{2y}-\vec P=0 \tag{II}
\end{gather}
\]
- x-direction:
\[
T_{1x}=T_1\sin 15° \tag{III}
\]
\[
T_{2x}=T_2\sin 15° \tag{IV}
\]
Note: Unlike the usual practice where the angle is measured relative to the
x-axis and the component in this direction is proportional to the cosine, here the angle was
measured relative to the y-axis, and the component is proportional to the sine of the angle.
- y-direção:
\[
T_{1y}=T_1\cos 15° \tag{V}
\]
\[
T_{2y}=T_2\cos 15° \tag{VI}
\]
The gravitational force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_g=mg} \tag{VII}
\end{gather}
\]
Substituting equations (III), (IV), (V), (VI), and (VII) into equation (II) and separating the components in
the x and y directions.
- x-direção:
\[
\begin{gather}
T_1\sin 15°-T_2\sin 15°=0
\end{gather}
\]
- y-direção:
\[
\begin{gather}
T_1\cos 15°+T_2\cos 15°-mg=0
\end{gather}
\]
these equations can be written as a system of two equations to two unknowns (T1 and
T2)
\[
\begin{gather}
\left\{
\begin{array}{l}
T_1\sin 15°-T_2\sin 15°=0\\
T_1\cos 15°+T_2\cos 15°-P=0
\end{array}
\right.
\end{gather}
\]
solving the first equation of the system for T1
\[
\begin{gather}
T_1\sin 15°-T_2\sin 15°=0 \\[5pt]
T_1\cancel{\sin 15°}=T_2\cancel{\sin 15°} \\[5pt]
T_1=T_2 \tag{VIII}
\end{gather}
\]
substituting the value of (VIII) into the second equation of the system
\[
\begin{gather}
T_2\cos 15°+T_2\cos 15°-mg=0 \\[5pt]
2 T_2\cos 15°=mg \\[5pt]
T_2=\frac{mg}{2\cos 15°}
\end{gather}
\]
substituting the given data
\[
\begin{gather}
T_2=\frac{(100\;\mathrm{kg})\left(9.8\;\mathrm{\frac{m}{s^2}}\right)}{2\times 0.966} \\[5pt]
T_2=507.3\;\mathrm N
\end{gather}
\]
using equality (III)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_1=T_2=507.3\;\mathrm N}
\end{gather}
\]
Now analyzing the forces acting at point D.
Drawing a horizontal line through point D, the angle between this line and rope \( \overline{AD} \) measures 45º is an internal angle with the angle between rope \( \overline{AD} \) and the ceiling (Figure 3-A).
The angle between rope \( \overline{BD} \) and the horizontal line measures 60°, which is an alternate angle with the angle between rope \( \overline{BD} \) and the ceiling.
Drawing a vertical line at point D, the angle between rope \( \overline{DE} \) and this line is 15º, which is an alternate angle with the angle found in the first part of the problem.

Drawing the forces at point D (Figure 3-B) in an xy coordinate system and decomposing the forces, tension force \( {\vec T}_{2} \) has already been determined, and has components \( {\vec T}_{2x} \) and \( {\vec T}_{2y} \). While the tension forces \( {\vec T}_{3} \) and \( {\vec T}_{4} \) have components \( {\vec T}_{3x} \) and \( {\vec T}_{4x} \) in the x direction and components \( {\vec T}_{3y} \) and \( {\vec T}_{4y} \) in the y direction.
Since the system is in equilibrium, we can apply condition (I)
\[
\begin{gather}
{\vec T}_2+{\vec T}_3+{\vec T}_4=0 \\[5pt]
{\vec T}_{2x}-{\vec T}_{2y}+{\vec T}_{3x}+{\vec T}_{3y}-{\vec T}_{4x}+{\vec T}_{4y}=0 \tag{IX}
\end{gather}
\]
- x-direction:
\[
T_{2x}=T_2\sin 15° \tag{X}
\]
\[
T_{3x}=T_3\cos 60° \tag{XI}
\]
\[
T_{4x}=T_4\cos 45° \tag{XII}
\]
- y-direction:
\[
T_{2y}=T_2\cos 15° \tag{XIII}
\]
\[
T_{3y}=T_3\sin 60° \tag{XIV}
\]
\[
T_{4y}=T_4\sin 45° \tag{XV}
\]
Substituting equations (X), (XI), (XII), (XIII), (XIV), and (XV) into equation (IX) and separating the
components in the x and y directions
- x-direction:
\[
\begin{gather}
T_2\sin 15°+T_3\cos 60°-T_4\cos 45°=0\\[5pt]
\end{gather}
\]
- y-direction:
\[
\begin{gather}
T_3\sin 60°+T_4\sin 45°-T_2\cos 15°=0
\end{gather}
\]
these equations can be written as a system of two equations to two unknowns (T3 and
T4)
Note: T2 is not an unknown as it has already been determined, so we move
the terms in T2 in both equations to the right-hand side of the equation.
\[
\begin{gather}
&\left\{
\begin{matrix}
T_2\sin 15°+T_3\cos 60°-T_4\cos 45°=0\\
T_3\sin 60°+T_4\sin 45°-T_2\cos 15°=0
\end{matrix}
\right.\\[8pt]
&\left\{
\begin{matrix}
T_3\cos 60°-T_4\cos 45°=-T_2\sin 15°\\
T_3\sin 60°+T_4\sin 45°=T_2\cos 15°
\end{matrix}
\right.
\end{gather}
\]
adding the two equations of the system, we eliminate the term in T4
\[
\begin{gather}
\frac{
\begin{matrix}
T_3\cos 60°-\cancel{T_4\cos 45°}=-T_2\sin 15°\\
T_3\sin 60°+\cancel{T_4\sin 45°}=T_2\cos 15°
\end{matrix}}
{T_3(\cos 60°+\sin 60°)+0=T_2(\cos 15°-\sin 15°)}\\[5pt]
T_3=\frac{\cos 15°-\sin 15°}{\cos 60°+\sin 60°}\,T_2
\end{gather}
\]
Note: remember that cos 45° is equal to sin 45°, so these terms cancel out when we add the
two equations, as they have opposite signs in the equations.
substituting the values given in the problem and the tension T2 determined above
\[
\begin{gather}
T_3=\frac{0.966-0.258}{0.500+0.866}\times 507.3\;\mathrm N
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_3=262.9\;\mathrm N}
\end{gather}
\]
Solving the second equation of the system for T4
\[
\begin{gather}
T_3\sin 60°+T_4\sin 45°=T_2\cos 15° \\[5pt]
T_4=\frac{T_2\cos 15°-T_3\sin 60°}{\sin 45°}
\end{gather}
\]
substituting the given values and the tensions T2 and T3 determined
above
\[
\begin{gather}
T_4=\frac{(507.3\;\mathrm N)\times 0.966-(262.9\;\mathrm N)\times 0.866}{0.707}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{T_4=371.1\;\mathrm N}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .