Exercício Resolvido de Estática
publicidade
Três cilindros A, B e C, com eixos horizontais e cada um de peso P, estão
em equilíbrio apoiados sobre um sistema de dois planos inclinados cada um deles de um ângulo de 30° em
relação à horizontal, como mostrado na Figura. Determinar as intensidades das forças de reação em cada
cilindro devido aos planos e aos demais cilindros.

Dados do problema:
- Peso de cada cilindro A, B e C: P;
- Ângulo entre o plano inclinado e a horizontal: 30°.
Isolamos os corpos e analisamos as forças que atuam em cada um deles.
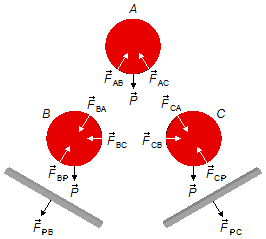
Cilindro A:
- \( \vec{P} \): força peso do cilindro;
- \( {\vec F}_{AB} \): força de contato no cilindro A devido ao cilindro B;
- \( {\vec F}_{AC} \): força de contato no cilindro A devido ao cilindro C.
- \( \vec{P} \): peso do cilindro;
- \( {\vec F}_{BA} \): força de contato no cilindro B devido ao cilindro A;
- \( {\vec F}_{BC} \): força de contato no cilindro B devido ao cilindro C;
- \( {\vec F}_{BP} \): força de contato no cilindro B devido ao plano.
- \( \vec{P} \): peso do cilindro;
- \( {\vec F}_{CA} \): força de contato no cilindro C devido ao cilindro A;
- \( {\vec F}_{CB} \): força de contato no cilindro C devido ao cilindro B;
- \( {\vec F}_{BP} \): força de contato no cilindro B devido ao plano.
- \( {\vec F}_{PB} \): força de contato no plano devido ao cilindro B;
- \( {\vec F}_{PC} \): força de contato no plano devido ao cilindro C.
Solução
O plano inclinado forma um ângulo de 30° com a horizontal, a força de reação \( \vec{F}_{BP} \) é normal ou perpendicular ao plano, forma um ângulo de 90°. Prolongando a direção da força de reação do plano inclinado até o plano horizontal ela forma um ângulo α (Figura 2 – destacado no retângulo em azul). O ângulo entre a força de reação e a horizontal também é α, são ângulos correspondentes. A soma dos ângulos internos de um triângulo é igual a 180°
\[
\begin{gather}
\alpha +30°+90°=180°\Rightarrow \alpha=180°-90°-30°\Rightarrow \alpha=60°
\end{gather}
\]

Supondo os três cilindros iguais eles possuem o mesmo raio, assim a distância entre seus centros a, b e c são iguais e determinam os lados de um triângulo equilátero com os três ângulos iguais. Como a soma dos ângulos internos de um triângulo é igual a 180°
\[
\begin{gather}
\beta +\beta +\beta =180°\Rightarrow 3\beta=180°\Rightarrow \beta =\frac{180°}{3}\Rightarrow\beta =60°
\end{gather}
\]
assim as forças de contato entre os cilindros A e B
(\( {\vec F}_{AB} \)
e
\( {\vec F}_{BA} \)),
A e C
(\( {\vec F}_{AC} \)
e
\( {\vec F}_{CA} \))
e entre o cilindro B ou C e os planos inclinados
(\( {\vec F}_{PB} \)
e
\( {\vec F}_{PC} \))
formam com a direção horizontal ângulos de 60°.Desenhando as forças num sistema de eixos coordenados xy podemos aplicar a condição de equilíbrio
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum F=0} \tag{I}
\end{gather}
\]
Cilindro A
- Direção x:
\[
\begin{gather}
F_{ABx}-F_{ACx}=0
\end{gather}
\]
temos
\( F_{ABx}=F_{AB}\cos 60° \)
e
\( F_{ACx}=F_{AC}\cos 60° \)
\[
\begin{gather}
F_{AB}\cos 60°-F_{AC}\cos 60°=0 \tag{II}
\end{gather}
\]
- Direção y:
\[
\begin{gather}
F_{ABy}+F_{ACy}-P=0
\end{gather}
\]
temos
\( F_{ABy}=F_{AB}\operatorname{sen}60° \)
e
\( F_{ACy}=F_{AC}\operatorname{sen}60° \)
\[
\begin{gather}
F_{AB}\operatorname{sen}60°+F_{AC}\operatorname{sen}60°-P=0 \tag{III}
\end{gather}
\]

Figura 3
Lembrando da Trigonometria
\[
\begin{gather}
\operatorname{sen}60°=\frac{\sqrt{3\,}}{2}
\end{gather}
\]
substituímos em (III)
\[
\begin{gather}
F_{AB}\frac{\sqrt{3\,}}{2}+F_{AB}\frac{\sqrt{3\,}}{2}-P=0\\[5pt]
2 F_{AB}\frac{\sqrt{3\,}}{2}=P\\[5pt]
F_{AB}\sqrt{3\,}=P\\[5pt]
F_{AB}=\frac{P}{\sqrt{3\,}}
\end{gather}
\]
multiplicando o numerador e o denominador por
\( \sqrt{3\,} \)
\[
\begin{gather}
F_{AB}=\frac{P}{\sqrt{3\,}}.\frac{\sqrt{3\,}}{\sqrt{3\,}}\\[5pt]
F_{AB}=\frac{\sqrt{3\,}}{3}P
\end{gather}
\]
Como as forças
\( {\vec F}_{AB} \)
e
\( {\vec F}_{BA} \)
são forças de ação e reação possuem a mesma intensidade e a mesma direção, mas com sentidos opostos,
da mesma forma para as forças
\( {\vec F}_{AC} \)
e
\( {\vec F}_{CA} \)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F_{AB}=F_{BA}=F_{AC}=F_{CA}=\frac{\sqrt{3\,}}{3}P}
\end{gather}
\]
Cilindro B
- Direção x:
\[
\begin{gather}
F_{BPx}-F_{BC}-F_{BAx}=0
\end{gather}
\]
temos
\( F_{BPx}=F_{BP}\cos 60° \)
e
\( F_{BAx}=F_{BA}\cos 60° \)
\[
\begin{gather}
F_{BP}\cos 60°-F_{BC}-F_{BA}\cos 60°=0
\end{gather}
\]
temos
\( F_{BA} \)
a intensidade da força de reação no cilindro B devido ao cilindro A, já determinada.
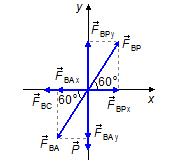
Figura 4
Lembrando da Trigonometria
\[
\begin{gather}
\cos 60°=\frac{1}{2}
\end{gather}
\]
\[
\begin{gather}
F_{BP}\frac{1}{2}-F_{BC}-\frac{\sqrt{3\,}}{3}P\frac{1}{2}=0\\[5pt]
\frac{1}{2}F_{BP}-F_{BC}=\frac{\sqrt{3\,}}{6}P \tag{IV}
\end{gather}
\]
- Direção y:
\[
\begin{gather}
F_{BPy}-F_{BAy}-P=0
\end{gather}
\]
temos
\( F_{BPy}=F_{BP}\operatorname{sen}60° \)
e
\( F_{BAy}=F_{BA}\operatorname{sen}60° \)
\[
\begin{gather}
F_{BP}\operatorname{sen}60°-F_{BA}\operatorname{sen}60°-P=0
\end{gather}
\]
usando o valor de
\( F_{BA} \)
e o seno de 60°
\[
\begin{gather}
F_{BP}\frac{\sqrt{3\,}}{2}-\frac{\sqrt{3\,}}{3}P\frac{\sqrt{3\,}}{2}-P=0\\[5pt]
\frac{\sqrt{3\,}}{2}F_{BP}-\frac{3}{3.2}P-P=0\\[5pt]
\frac{\sqrt{3\,}}{2}F_{BP}-\frac{1}{2}P-P=0
\end{gather}
\]
multiplicando a expressão acima por 2
\[
\begin{gather}
\qquad\; \frac{\sqrt{3\,}}{2}F_{BP}-\frac{1}{2}P-P=0 \quad \text{(}\times\text{2)}\\[5pt]
\sqrt{3\,}F_{BP}-P-2P=0\\[5pt]
\sqrt{3\,}F_{BP}-3P=0\\[5pt]
\sqrt{3\,}F_{BP}=3P\\[5pt]
F_{BP}=\frac{3P}{\sqrt{3\,}}
\end{gather}
\]
multiplicando o numerador e o denominador por
\( \sqrt{3\,} \)
\[
\begin{gather}
F_{BP}=\frac{3P}{\sqrt{3\,}}\frac{\sqrt{3\,}}{\sqrt{3\,}}\\[5pt]
F_{BP}=\sqrt{3\,}P
\end{gather}
\]
Como as forças
\( {\vec F}_{BP} \)
e
\( {\vec F}_{PB} \)
são forças de ação e reação possuem a mesma intensidade e a mesma direção, mas com sentidos opostos,
da mesma forma para as forças
\( {\vec F}_{CP} \)
e
\( {\vec F}_{PC} \)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F_{BP}=F_{PB}=F_{CP}=F_{PC}=\sqrt{3\,}P}
\end{gather}
\]
substituindo este valor na expressão (IV)
\[
\begin{gather}
\frac{1}{2}\,\sqrt{3\,}P-F_{BC}=\frac{\sqrt{3\,}}{6}P\\[5pt]
F_{BC}=\frac{\sqrt{3\,}}{2}P-\frac{\sqrt{3\,}}{6}P
\end{gather}
\]
multiplicando e dividindo por 3 o primeiro termo do lado direito da igualdade
\[
\begin{gather}
F_{BC}=\frac{3}{3}.\frac{\sqrt{3\,}}{2}P-\frac{\sqrt{3\,}}{6}P\\[5pt]
F_{BC}=\frac{3\sqrt{3\,}P-\sqrt{3\,}P}{6}\\[5pt]
F_{BC}=\frac{2\sqrt{3\,}}{6}P\\[5pt]
F_{BC}=\frac{\sqrt{3\,}}{3}P
\end{gather}
\]
Como as forças
\( {\vec F}_{BC} \)
e
\( {\vec F}_{CB} \)
são forças de ação e reação possuem a mesma intensidade e a mesma direção, mas com sentidos opostos
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F_{BC}=F_{CB}=\frac{\sqrt{3\,}}{3}P}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .