Solved Problem on Static Equilibrium
advertisement   



Three cylinders A, B, and C, with the horizontal axis and each weight W, are in equilibrium on a system of two inclined planes, each with an angle of 30° relative to a plane, as shown in the figure. Determine the magnitudes of reaction forces in each cylinder due to planes and other cylinders.


Problem data:
  • Weight of each cylinder A, B and C:    W;
  • Angle between the inclined and horizontal plane:    30°.
Problem diagram:

Drawing a free-bodies diagrams, we have the forces that act in each body.

Figure 1

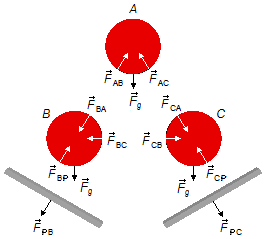
Cylinder A:
  • \( {\vec F}_{g} \): gravitational force;
  • \( {\vec F}_{AB} \): contact force on cylinder A due to the cylinder B;
  • \( {\vec F}_{AC} \): contact force on cylinder A due to the cylinder C.
Cylinder B:
  • \( {\vec F}_{g} \): gravitational force;
  • \( {\vec F}_{BA} \): contact force on cylinder B due to cylinder A;
  • \( {\vec F}_{BC} \): contact force on cylinder B due to cylinder C;
  • \( {\vec F}_{BP} \): contact force on cylinder B due to the plane.
Cylinder C:
  • \( {\vec F}_{g} \): gravitational force;
  • \( {\vec F}_{CA} \): contact force on cylinder C due to cylinder A;
  • \( {\vec F}_{CB} \): contact force on cylinder C due to cylinder B;
  • \( {\vec F}_{BP} \): contact force on cylinder B due to the plane.
Inclined planes:
  • \( {\vec F}_{PB} \): contact force on the plan due to cylinder B;
  • \( {\vec F}_{PC} \): contact force on the plane due to cylinder C.
The weights of the planes were neglected

Solution

The inclined plane makes an angle of 30° with the horizontal, the reaction force \( \vec{F}_{BP} \) is normal or perpendicular to the plane, making a 90° angle. Extending the line in the direction of the reaction force of the inclined plane to the horizontal plane, making an angle α (Figure 2 - highlighted in the blue rectangle). The angle between the reaction force and the horizontal is also α, are corresponding angles. As the sum of the interior angles of a triangle is equal to 180°
\[ \begin{gather} \alpha +30°+90°=180°\Rightarrow \alpha=180°-90°-30°\Rightarrow \alpha=60° \end{gather} \]
Figure 2

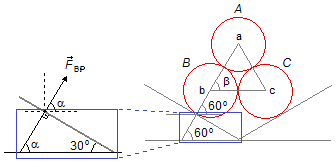
Assuming the three cylinders are equals, they have the same radius, so the distance between their centers a, b, and c are equal and determine the sides of an equilateral triangle with the three equal angles. As the sum of the interior angles of a triangle is equal to 180°
\[ \begin{gather} \beta +\beta +\beta =180°\Rightarrow 3\beta=180°\Rightarrow \beta =\frac{180°}{3}\Rightarrow\beta =60° \end{gather} \]
thus the contact forces between cylinders A and B (\( {\vec F}_{AB} \) and \( {\vec F}_{BA} \)), A and C (\( {\vec F}_{AC} \) and \( {\vec F}_{CA} \)), and between cylinder B or C and inclined planes (\( {\vec F}_{PB} \) and \( {\vec F}_{PC} \)) make with the horizontal direction a 60° angle.
Drawing the forces in a coordinate system xy, we can apply the equilibrium condition
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum F=0} \tag{I} \end{gather} \]
Cylinder A
  • Direction x:
\[ \begin{gather} F_{ABx}-F_{ACx}=0 \end{gather} \]
we have \( F_{ABx}=F_{AB}\cos 60° \) and \( F_{ACx}=F_{AC}\cos 60° \)
\[ \begin{gather} F_{AB}\cos 60°-F_{AC}\cos 60°=0 \tag{II} \end{gather} \]
  • Direction y:
\[ \begin{gather} F_{ABy}+F_{ACy}-W=0 \end{gather} \]
we have \( F_{ABy}=F_{AB}\sin 60° \) and \( F_{ACy}=F_{AC}\sin 60° \)
\[ \begin{gather} F_{AB}\sin 60°+F_{AC}\sin 60°-W=0 \tag{III} \end{gather} \]

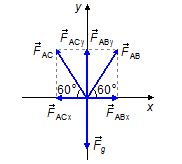
Figure 3

As all cylinders have the same weight the magnitudes of reaction forces \( {\vec F}_{AB} \) and \( {\vec F}_{AC} \) will be the same, and in different directions, FAB=FAC

From the Trigonometry
\[ \begin{gather} \sin 60°=\frac{\sqrt{3\,}}{2} \end{gather} \]

we have substituted in (III)
\[ \begin{gather} F_{AB}\frac{\sqrt{3\,}}{2}+F_{AB}\frac{\sqrt{3\,}}{2}-W=0\\[5pt] 2 F_{AB}\frac{\sqrt{3\,}}{2}=W\\[5pt] F_{AB}\sqrt{3\,}=W\\[5pt] F_{AB}=\frac{W}{\sqrt{3\,}} \end{gather} \]
multiplying the numerator and the denominator by \( \sqrt{3\,} \)
\[ \begin{gather} F_{AB}=\frac{W}{\sqrt{3\,}}\times\frac{\sqrt{3\,}}{\sqrt{3\,}}\\[5pt] F_{AB}=\frac{\sqrt{3\,}}{3}W \end{gather} \]
As \( {\vec F}_{AB} \) and \( {\vec F}_{BA} \) forces are a pair of action-reaction forces, they have the same magnitude but in opposite directions, as the forces \( {\vec F}_{AC} \) and \( {\vec F}_{CA} \)
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{AB}=F_{BA}=F_{AC}=F_{CA}=\frac{\sqrt{3\,}}{3}W} \end{gather} \]
Cylinder B
  • Direction x:
\[ \begin{gather} F_{BPx}-F_{BC}-F_{BAx}=0 \end{gather} \]
we have \( F_{BPx}=F_{BP}\cos 60° \) and \( F_{BAx}=F_{BA}\cos 60° \)
\[ \begin{gather} F_{BP}\cos 60°-F_{BC}-F_{BA}\cos 60°=0 \end{gather} \]
we have \( F_{BA} \) the magnitude of the reaction force on cylinder B due to cylinder A already determined.

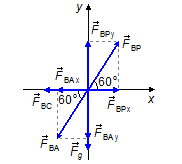
Figure 4

From the Trigonometry
\[ \begin{gather} \cos 60°=\frac{1}{2} \end{gather} \]
\[ \begin{gather} F_{BP}\frac{1}{2}-F_{BC}-\frac{\sqrt{3\,}}{3}W\frac{1}{2}=0\\[5pt] \frac{1}{2}F_{BP}-F_{BC}=\frac{\sqrt{3\,}}{6}W \tag{IV} \end{gather} \]
  • Direction y:
\[ \begin{gather} F_{BPy}-F_{BAy}-W=0 \end{gather} \]
we have \( F_{BPy}=F_{BP}\sin 60° \) and \( F_{BAy}=F_{BA}\sin 60° \)
\[ \begin{gather} F_{BP}\sin 60°-F_{BA}\sin 60°-W=0 \end{gather} \]
using the value of \( F_{BA} \) the sine of 60°
\[ \begin{gather} F_{BP}\frac{\sqrt{3\,}}{2}-\frac{\sqrt{3\,}}{3}W\frac{\sqrt{3\,}}{2}-W=0\\[5pt] \frac{\sqrt{3\,}}{2}F_{BP}-\frac{3}{3\times 2}W-W=0\\[5pt] \frac{\sqrt{3\,}}{2}F_{BP}-\frac{1}{2}W-W=0 \end{gather} \]
multiplying the expression up by 2
\[ \begin{gather} \qquad\; \frac{\sqrt{3\,}}{2}F_{BP}-\frac{1}{2}W-W=0 \quad \text{(}\times\text{2)}\\[5pt] \sqrt{3\,}F_{BP}-W-2W=0\\[5pt] \sqrt{3\,}F_{BP}-3W=0\\[5pt] \sqrt{3\,}F_{BP}=3W\\[5pt] F_{BP}=\frac{3W}{\sqrt{3\,}} \end{gather} \]
multiplying the numerator and the denominator by \( \sqrt{3\,} \)
\[ \begin{gather} F_{BP}=\frac{3W}{\sqrt{3\,}}\times \frac{\sqrt{3\,}}{\sqrt{3\,}}\\[5pt] F_{BP}=\sqrt{3\,}W \end{gather} \]
As \( {\vec F}_{BP} \) and \( {\vec F}_{PB} \) forces are a pair of action-reaction forces, they have the same magnitude but in opposite directions, as the forces \( {\vec F}_{CP} \) and \( {\vec F}_{PC} \)
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{BP}=F_{PB}=F_{CP}=F_{PC}=\sqrt{3\,}W} \end{gather} \]
substituting this value into the expression (IV)
\[ \begin{gather} \frac{1}{2}\,\sqrt{3\,}W-F_{BC}=\frac{\sqrt{3\,}}{6}W\\[5pt] F_{BC}=\frac{\sqrt{3\,}}{2}W-\frac{\sqrt{3\,}}{6}W \end{gather} \]
multiplying and dividing by 3 the first term on the right-hand side of the equation
\[ \begin{gather} F_{BC}=\frac{3}{3}\times\frac{\sqrt{3\,}}{2}W-\frac{\sqrt{3\,}}{6}W\\[5pt] F_{BC}=\frac{3\sqrt{3\,}W-\sqrt{3\,}W}{6}\\[5pt] F_{BC}=\frac{2\sqrt{3\,}}{6}W\\[5pt] F_{BC}=\frac{\sqrt{3\,}}{3}W \end{gather} \]
As \( {\vec F}_{BC} \) and \( {\vec F}_{CB} \) forces are a pair of action-reaction forces, they have the same magnitude but in opposite directions
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{BC}=F_{CB}=\frac{\sqrt{3\,}}{3}W} \end{gather} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .