Um corpo encontra-se sobre um plano inclinado de um ângulo α com a horizontal. Para movê-lo para cima é necessária uma força paralela à superfície inclinada cuja intensidade mínima é F₁, e para evitar seu deslizamento para baixo é necessária uma força de intensidade mínima F₂, também paralela ao declive. Sendo F₁=2F₂, calcular o coeficiente de atrito entre o corpo e o plano.


Dados do problema:

• Ângulo de inclinação do plano:    α;
• Força necessária para fazer o corpo subir:    F₁;
• Força necessária para impedir o corpo de descer:    F₂.

Esquema do problema:

Consideramos que o corpo ainda não está se movendo, na primeira situação, quando a força F₁ é aplicada, o corpo está na iminência de subir (não confundir iminência com eminência). Devido à força aplicada o corpo atua no plano e o plano reage com a força de atrito de intensidade F_at, como o corpo está prestes a subir a força de atrito tem sentido contrário do movimento, para baixo na direção do plano (Figura 1-A).


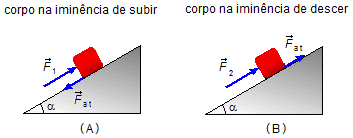
Na segunda situação quando a força F₂ é aplicada o corpo está na iminência de descer. Devido à força aplicada atua no plano e o plano reage com a força de atrito de intensidade F_at como o corpo está prestes a descer a força de atrito tem sentido contrário do movimento, para cima na direção do plano (Figura 1-B).

Solução

Isolamos o corpo e pesquisamos as forças que atuam nele.
Adotamos um sistema de referência com o eixo-x paralelo ao plano e com sentido ascendente e o eixo-y para cima perpendicular ao plano.

Corpo na iminência de subir (Figura 2-A)

• \( {\vec F}_{1} \): força aplicada ao corpo;
• \( {\vec F}_{at} \): força de atrito entre o corpo e o plano;
• \( \vec{P} \): força peso;
• \( \vec{N} \): força normal de reação do plano sobre o corpo.

A força peso \( \vec{P} \) pode ser decomposta em duas componentes, uma componente paralela \( {\vec P}_{P} \) ao eixo-x e a outra normal ou perpendicular \( {\vec P}_{N} \). No triângulo à esquerda na Figura 2-B vemos que a força peso é perpendicular ao plano horizontal, forma um ângulo de 90°, o ângulo entre o plano inclinado e o plano horizontal é igual á α, o ângulo entre a força peso e a componente paralela será β, como os ângulos internos de um triângulo devem somar 180° No triângulo à direita temos que a componente normal faz com o plano inclinado um ângulo de 90°, então o ângulo entre a força peso e a componente normal deve medir α, é um ângulo complementar.


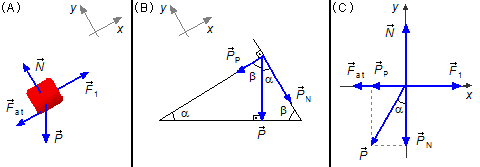
Desenhando as forças num sistema de eixos coordenados xy podemos aplicar a condição de equilíbrio Direção x: a componente paralela da força peso e a força de atrito são dadas por onde μ é o coeficiente de atrito entre o bloco e o plano, substituindo estas expressões na expressão (II) Direção y: a componente normal da força peso é dada por substituindo a expressão (VII) na expressão (VI) substituindo a expressão (VIII) na expressão (V) Corpo na iminência de descer (Figura 3-A)

• \( {\vec F}_{2} \): força aplicada ao corpo;
• \( {\vec F}_{at} \): força de atrito entre o corpo e o plano;
• \( \vec{P} \): força peso;
• \( \vec{N} \): força normal de reação do plano sobre o corpo.

A força peso pode ser decomposta da mesma maneira mostrada na Figura 2-B.
Desenhando as forças num sistema de eixos coordenados xy podemos aplicar a condição de equilíbrio (I)


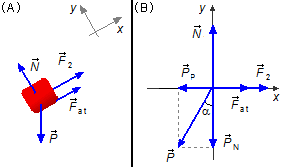
Direção x: substituindo as expressões (III) e (IV) na expressão (X) Direção y: a componente normal da força peso é dada por substituindo na expressão (XII) substituindo a expressão (XIII) na expressão (XI) Usando a condição dada no problema, \( F_{1}=2F_{2} \), substituímos as expressões (IX) e (XIV)