Solved Problem on Static Equilibrium

A body lies over an inclined plane of an angle α with the horizontal. To move upward it is required a force parallel to the inclined plane whose minimum magnitude is F₁ To prevent the body from sliding down is required a force whose minimum magnitude is F₂, also parallel to the slope. If F₁ = 2F₂, calculate the coefficient of friction between the body and the plane.

Problem data:

Angle of inclination: α;
Force to make the body rise: F₁;
Force to prevent the body from descending: F₂.

Problem diagram:

We consider that the body is still not moving, in the first case, when the force F₁ is applied, the body is about to rise. Due to the applied force, the body acts in the plane, the plane reacts with the friction force of magnitude F_f, as the body is about to climb, the friction force is in the opposite direction of the motion, in a downward direction (Figure 1-A ).

Figure 1

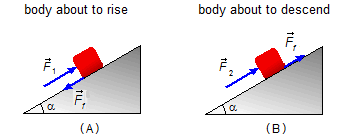
In the second case, when the force F₂ is applied, the body is about to descend. Due to the applied force, the body acts in the plane, the plane reacts with the friction force of magnitude F_at, as the body is about to descend the friction force is in the opposite direction of the motion, in an upward direction (Figure 1-B).

Solution

Drawing a free-body diagram, we have the forces that act on it.
We chose a reference frame with the x-axis parallel to the plane in the upward direction and the y-axis perpendicular to the plane.

Body about to rise (Figure 2-A)

\( {\vec F}_{1} \): force applied to the body;
\( {\vec F}_{f} \): force of friction between the body and the plane;
\( {\vec F}_{g} \): gravitational force;
\( \vec{N} \): normal reaction force of the plane on the body.

The gravitational force \( {\vec F}_{g} \) can be decomposed into two components, a component parallel to the x-axis \( {\vec F}_{gP} \), and a component normal or perpendicular \( {\vec F}_{gN} \). In the triangle to the left in Figure 2-B, we see that the gravitational force is perpendicular to the horizontal plane, makes a 90° angle, the angle between the inclined plane and the horizontal plane is equal to the α, the angle between gravitational force and the parallel component will be β, as the sum of the interior angles of a triangle is equal to 180°

\[ \begin{gather} \alpha +\beta +90°=180°\Rightarrow \alpha=180°-90°-\alpha \Rightarrow \alpha=90°-\alpha \end{gather} \]

In the triangle to the right, the normal component makes with the inclined plane a 90° angle, then the angle between the gravitational force and the normal component measure α, is a complementary angle.

Figure 2

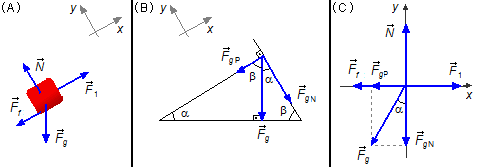
Drawing the forces in a coordinate system xy, we can apply the equilibrium condition

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum F=0} \tag{I} \end{gather} \]

Direction x:

\[ \begin{gather} F_{1}-F_{gP}-F_{f}=0 \tag{II} \end{gather} \]

the parallel component of gravitational force and friction force are given by

\[ \begin{gather} F_{gP}=F_{g}\sin \alpha \tag{III} \end{gather} \]

\[ \begin{gather} F_{f}=\mu N \tag{IV} \end{gather} \]

where μ is the coefficient of friction between the block and the plane, substituting these expressions into expression (II)

\[ \begin{gather} F_{1}-F_{g}\sin \alpha -\mu N=0 \tag{V} \end{gather} \]

Direction y:

\[ \begin{gather} N-F_{gN}=0 \tag{VI} \end{gather} \]

the normal component of gravitational force given by

\[ \begin{gather} F_{gN}=F_{g}\cos \alpha \tag{VII} \end{gather} \]

substituting this expression into expression (VI)

\[ \begin{gather} N-F_{g}\cos \alpha =0\\[5pt] N=F_{f}\cos \alpha\tag{VIII} \end{gather} \]

substituting the expression (VII) into expression (V)

\[ \begin{gather} F_{1}-F_{g}\sin \alpha -\mu F_{g}\cos \alpha=0\\[5pt] F_{1}=F_{g}\sin \alpha +\mu F_{g}\cos \alpha\\[5pt] F_{1}=F_{g}(\sin \alpha +\mu \cos \alpha ) \tag{IX} \end{gather} \]

Body about to descend (Figure 3-A)

\( {\vec F}_{2} \): force applied to the body;
\( {\vec F}_{f} \): force of friction between the body and the plane;
\( {\vec F}_{g} \): gravitational force;
\( \vec{N} \): normal reaction force of the plane on the body.

The gravitational force can be decomposed in the same way shown in Figure 2-B.
Drawing the forces in a coordinate system xy, we can apply the equilibrium condition (I)

Figure 3

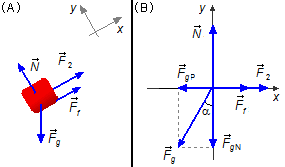
Direction x:

\[ \begin{gather} F_{2}+F_{f}-F_{gP}=0 \tag{X} \end{gather} \]

substituting expressions (III) and (IV) into expression (X)

\[ \begin{gather} F_{2}+\mu N-F_{g}\sin \alpha =0 \tag{XI} \end{gather} \]

Direction y:

\[ \begin{gather} N-F_{gN}=0 \tag{XII} \end{gather} \]

the normal component of gravitational force is given by

\[ \begin{gather} F_{gN}=F_{g}\cos \alpha \end{gather} \]

substituting this expression into expression (XII)

\[ \begin{gather} N-F_{g}\cos \alpha =0\\[5pt] N=F_{g}\cos \alpha \tag{XIII} \end{gather} \]

substituting the expression (XIII) into expression (XI)

\[ \begin{gather} F_{2}+\mu F_{g}\cos \alpha -F_{g}\sin \alpha=0\\[5pt] F_{2}=F_{g}\sin \alpha -\mu F_{g}\cos \alpha\\[5pt] F_{2}=F_{g}(\sin \alpha -\mu \cos \alpha) \tag{XIV} \end{gather} \]

Using the condition given in the problem \( F_{1}=2F_{2} \), we substitute the expressions (IX) and (XIV)

\[ \begin{gather} \cancel{F_{g}}(\sin \alpha +\mu \cos \alpha)=2\,\cancel{F_{g}}\,(\sin \alpha -\mu \cos \alpha)\\[5pt] \sin \alpha +\mu \cos \alpha=2\,(\,\sin \alpha -\mu \cos \alpha \,) \\[5pt] \sin \alpha+\mu \cos \alpha =2\,\sin \alpha -2\,\mu \cos \alpha \\[5pt] \mu \cos \alpha +2\,\mu \cos \alpha =2\,\sin \alpha -\sin\alpha \\[5pt] 3\,\mu \cos \alpha =\sin \alpha \\[5pt] \mu=\frac{1}{3}\,\frac{\sin \alpha }{\cos \alpha } \end{gather} \]

From the Trigonometry \( \tan \alpha =\frac{\sin \alpha }{\cos \alpha } \)

\[ \begin{gather} \bbox[#FFCCCC,10px] {\mu =\frac{1}{3}\,\tan \alpha} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .