Exercício Resolvido de Dinâmica

Em um plano áspero inclinado de 45º em relação ao horizonte AB é a reta de maior declive. Um corpo é lançado no sentido ascendente entra em repouso em B retornando ao ponto A. O coeficiente de atrito entre o móvel e o plano é \( 2-\sqrt{3\;} \). Determinar a relação entre o intervalo de tempo empregado pelo corpo para ir de A até B e no retorno de B até A.

Dados do problema:

Coeficiente de atrito entre o móvel e o plano: \( \mu=2-\sqrt{3\;} \);
Inclinação do plano: θ = 45°.

Esquema do problema:

Figura 1

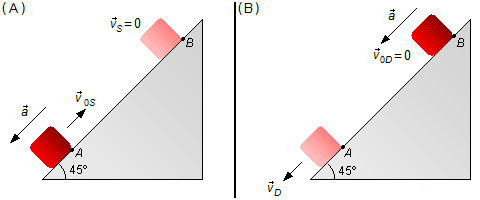
O corpo é lançado com uma velocidade inicial de subida v_0S e começa a desacelerar devido a componente da força peso na direção do plano, sua velocidade diminui até ficar nula, v_S = 0, no ponto B (Figura 1-A). A partir desse instante ele começa um movimento de retorno, partindo do repouso, v_0D = 0, e sob a ação da aceleração, causada pela componente da força peso direção do plano, e passa pelo ponto A com uma velocidade final v_D (Figura 1-B).

Solução:

Isolamos o corpo e analisamos as forças que atuam nele em cada uma das situações.

Corpo subindo:

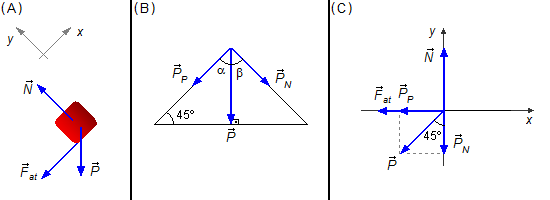
Adotamos um sistema de referência xy com o eixo-x paralelo ao plano inclinado e sentido para cima (Figura 2-A). No corpo atuam a força peso \( \vec P \), a força de atrito \( {\vec F}_{at} \) e a força normal de reação da superfície \( \vec N \).

Figura 2

A força peso pode ser decomposta em duas componentes, uma componente paralela ao eixo-x \( {\vec P}_{\small P} \) e a outra componente normal ou perpendicular \( {\vec P}_{\small N} \) (Figura 2-B).
No triângulo à esquerda a força peso \( \vec P \) é perpendicular ao plano horizontal, forma um ângulo de 90°, o ângulo entre o plano inclinado e o plano horizontal é dado como 45°, como os ângulos internos de um triângulo devem somar 180°, o ângulo α entre a força peso \( \vec P \) e a componente paralela \( {\vec P}_{\small P} \) será

\[ \begin{gather} 45°+90°+\alpha=180°\Rightarrow\alpha=180°-45°-90°\Rightarrow\alpha=45° \end{gather} \]

No triângulo à direita a componente normal da força peso \( {\vec P}_{\small N} \) faz com o plano inclinado um ângulo de 90°, o ângulo β entre a força peso \( \vec P \) e a componente normal \( {\vec P}_{\small N} \) será

\[ \begin{gather} \alpha+\beta=90°\Rightarrow 45°+\beta=90°\Rightarrow \beta=90°-45°\Rightarrow \beta=45° \end{gather} \]

são ângulos complementares.
Desenhamos as forças num sistema de eixos coordenados xy (Figura 2-C) e aplicamos a 2.ª Lei de Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \tag{I} \end{gather} \]

Na direção y não há movimento, a força normal de reação \( \vec N \) e a componente normal do peso \( {\vec P}_{\small N} \) se anulam

\[ \begin{gather} N=P_{\small N} \tag{II} \end{gather} \]

a componente normal do peso é dada por

\[ \begin{gather} P_{\small N}=P\cos 45° \tag{III} \end{gather} \]

a força peso do corpo é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{IV} \end{gather} \]

substituindo a equação (IV) na equação (III)

\[ \begin{gather} P_{\small N}=mg\cos 45° \tag{V} \end{gather} \]

substituindo a equação (V) na equação (II)

\[ \begin{gather} N=mg\cos 45° \tag{VI} \end{gather} \]

Na direção x aplicamos a equação (I) para encontrar a aceleração do bloco subindo a_S

\[ \begin{gather} -F_{at}-P_{\small P}=ma_{\small S} \tag{VII} \end{gather} \]

a força de atrito é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{at}=\mu N} \tag{VIII} \end{gather} \]

substituindo a equação (VI) na equação (VIII)

\[ \begin{gather} F_{at}=\mu mg\cos 45° \tag{IX} \end{gather} \]

a componente paralela do peso é dada por

\[ \begin{gather} P_{\small P}=P\operatorname{sen}45° \tag{X} \end{gather} \]

substituindo a equação (IV) na equação (X)

\[ \begin{gather} P_{\small P}=mg\operatorname{sen}45° \tag{XI} \end{gather} \]

substituindo as equações (IX) e (XI) na equação (VII)

\[ \begin{gather} -\mu \cancel mg\cos 45°-\cancel mg\cos 45°=\cancel ma_{\small S} \end{gather} \]

Da Trigonometria

\[ \begin{gather} \operatorname{sen}45°=\cos 45°=\dfrac{\sqrt{2\;}}{2} \end{gather} \]

\[ \begin{gather} -\mu g\frac{\sqrt{2\;}}{2}-g\frac{\sqrt{2\;}}{2}=a_{\small S} \\[5pt] a_{\small S}=-{\frac{\sqrt{2\;}}{2}}g(\mu+1) \tag{XII} \end{gather} \]

Corpo descendo:

Adotamos um sistema de referência xy com o eixo-x paralelo ao plano inclinado e sentido para baixo. No bloco atuam as mesmas forças, apenas a força de atrito \( {\vec F}_{at} \) está no sentido contrário (Figura 3-A).
Do mesmo modo a força peso pode ser decomposta em duas componentes (Figura 2-B).
Desenhamos as forças num sistema de eixos coordenados (Figura 3-B).
Na direção y é válida a mesma equação (VI) encontrada anteriormente.

Figura 3

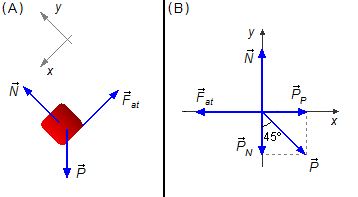
Na direção x aplicamos a 2.ª Lei de Newton

\[ \begin{gather} -F_{at}+P_{\small P}=ma_{\small D} \tag{XIII} \end{gather} \]

substituindo as equações (IX) e (XI) na equação (XIII)

\[ \begin{gather} -\mu \cancel mg\cos 45°+\cancel mg\cos 45°=\cancel ma_{\small D} \\[5pt] -\mu g\frac{\sqrt{2\;}}{2}+g\frac{\sqrt{2\;}}{2}=a_{\small D} \\[5pt] a_{\small D}=\frac{\sqrt{2\;}}{2}g(1-\mu) \tag{XIV} \end{gather} \]

Da Cinemática Escalar temos a função horária da velocidade

\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0+at} \end{gather} \]

Para o bloco subindo, a velocidade final é nula, v_S = 0, e substituindo a equação (XII)

\[ \begin{gather} v_{\small S}=v_{0\small S}+a_{\small S}t_{\small S} \\[5pt] 0=v_{0\small S}-{\frac{\sqrt{2\;}}{2}}g(\mu+1)t_{\small S} \\[5pt] v_{0\small S}=\frac{\sqrt{2\;}}{2}g(\mu+1)t_{\small S} \tag{XV} \end{gather} \]

Para o bloco descendo, a velocidade inicial é nula, v_0D = 0, e substituindo a equação (XIV)

\[ \begin{gather} v_{\small D}=v_{0\small D}+a_{\small D}t_{\small D} \\[5pt] v_{\small D}=0+\frac{\sqrt{2\;}}{2}g(1-\mu)t_{\small D} \\[5pt] v_{\small D}=\frac{\sqrt{2\;}}{2}g(1-\mu)t_{\small D} \tag{XVI} \end{gather} \]

Dividindo a equação (XV) pela equação (XVI)

\[ \begin{gather} \frac{v_{0\small S}}{v_{\small D}}=\frac{\dfrac{\cancel{\sqrt{2\;}}}{\cancel 2}\cancel g(\mu+1)t_{\small S}}{\dfrac{\cancel{\sqrt{2\;}}}{\cancel 2}\cancel g(1-\mu)t_{\small D}} \\[5pt] \frac{v_{0\small S}}{v_{\small D}}=\frac{(\mu+1)t_{\small S}}{(1-\mu)t_{\small D}} \tag{XVII} \end{gather} \]

Para encontrarmos as velocidades usamos a Equação de Torricelli

\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]

A distância percorrida pelo bloco é a mesma na subida e descida.
Durante a subida, substituindo a equação (XII)

\[ \begin{gather} v_{\small S}^2=v_{0\small S}^2+2a_{\small S}\Delta S \\[5pt] 0^2=v_{0S}^2-\cancel 2{\frac{\sqrt{2\;}}{\cancel 2}}g(\mu+1)\Delta S \\[5pt] v_{0\small S}^2=\sqrt{2\;}g(\mu+1)\Delta S \\[5pt] v_{0\small S}=\sqrt{\sqrt{2\;}g(\mu+1)\Delta S\;} \tag{XVIII} \end{gather} \]

Durante a descida, substituindo a equação (XIV)

\[ \begin{gather} v_{\small D}^2=v_{0\small D}^2+2a_{\small D}\Delta S \\[5pt] v_{\small D}^2=0^2+\cancel 2\frac{\sqrt{2\;}}{\cancel 2}g(1-\mu)\Delta S \\[5pt] v_{\small D}^2=\sqrt{2\;}g(1-\mu)\Delta S \\[5pt] v_{\small D}=\sqrt{\sqrt{2\;}g(1-\mu)\Delta S\;} \tag{XIX} \end{gather} \]

Substituindo as equações (XVIII) e (XIX) na equação (XVII)

\[ \begin{gather} \frac{\sqrt{\sqrt{2\;}g(\mu+1)\Delta S\;}}{\sqrt{\sqrt{2\;}g(1-\mu)\Delta S\;}}=\frac{(\mu+1)t_{\small S}}{(1-\mu)t_{\small D}} \end{gather} \]

elevando ao quadrado ambos os lados da equação

\[ \begin{gather} \left(\frac{\sqrt{\sqrt{2\;}g(\mu+1)\Delta S\;}}{\sqrt{\sqrt{2\;}g(1-\mu)\Delta S\;}}\right)^2=\left(\frac{(\mu+1)t_{\small S}}{(1-\mu)t_{\small D}}\right)^2 \\[5pt] \frac{\cancel{\sqrt{2\;}}\cancel g\cancel{(\mu+1)}\cancel{\Delta S}}{\cancel{\sqrt{2\;}}\cancel g\cancel{(1-\mu)}\cancel{\Delta S}}=\frac{(\mu+1)^{\cancel 2}t_{\small S}^2}{(1-\mu)^{\cancel 2}t_{\small D}^2} \\[5pt] 1=\frac{(\mu+1)t_{S}^2}{(1-\mu)t_{\small D}^2} \end{gather} \]

\[ \begin{gather} \left(\frac{t_{\small S}}{t_{\small D}}\right)^2=\frac{1-\mu}{(\mu+1)} \end{gather} \]

substituindo o valor de μ dado no problema

\[ \begin{gather} \left(\frac{t_{\small S}}{t_{D}}\right)^2=\frac{1-(2-\sqrt{3\;})}{2-\sqrt{3}+1} \\[5pt] \left(\frac{t_{\small S}}{t_{\small D}}\right)^2=\frac{1-2+\sqrt{3\;}}{3-\sqrt{3\;}} \\[5pt] \left(\frac{t_{\small S}}{t_{\small D}}\right)^2=\frac{-1+\sqrt{3\;}}{3-\sqrt{3\;}} \end{gather} \]

para racionalizar essa expressão multiplicamos o numerador e o denominador por \( 3+\sqrt{3\;} \)

\[ \begin{gather} \left(\frac{t_{\small S}}{t_{\small D}}\right)^2=\frac{-1+\sqrt{3\;}}{3-\sqrt{3\;}}\times\frac{3+\sqrt{3\;}}{3+\sqrt{3\;}} \\[5pt] \left(\frac{t_{\small S}}{t_{\small D}}\right)^2=\frac{-3-\sqrt{3\;}+3\sqrt{3\;}+3}{9+3\sqrt{3\;}-3\sqrt{3\;}-3} \\[5pt] \left(\frac{t_{\small S}}{t_{\small D}}\right)^2=\frac{2\sqrt{3\;}}{6} \\[5pt] \left(\frac{t_{\small S}}{t_{D}}\right)^2=\frac{\sqrt{3\;}}{3} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\frac{t_{\small S}}{t_{\small D}}=\sqrt{\frac{\sqrt{3\;}}{3}}} \end{gather} \]