Solved Problem on Dynamics

In an inclined plane AB of 45º to the horizontal, a body is launched in an upward direction rests for an instant returning to point A. The coefficient of friction between the block and the plane is \( 2-\sqrt{3\;} \). Determine the ratio between the interval of time to the body go from A to B and to return from B to A.

Problem data:

Coefficient of friction between the block and the plane: \( \mu =2-\sqrt{3\;} \);
Angle of inclined plane: θ = 45°.

Problem diagram:

Figure 1

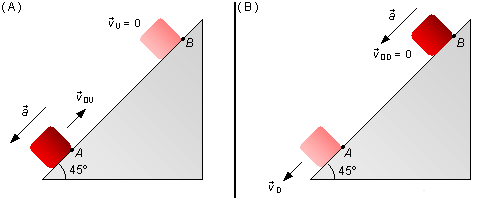
The body is launched with an initial speed v_0U and starts decelerating due to the component of gravitational force in the direction of the plane, its speed decreases until zero, v_U = 0 at point B (Figure 1-A). From this instant of time, it gets a return movement, starting from the rest v_0D = 0 and under the action of the acceleration due to the component of gravitational force and passes point A with a final speed v_D (Figure 1-B).

Solution

Drawing a free-body diagram, we have the forces that act in it in each situation.

Body rising:

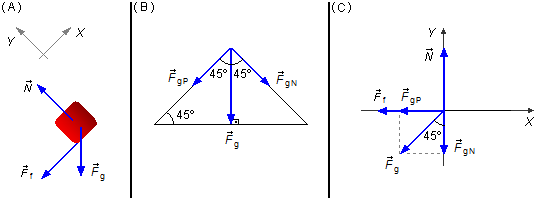
We choose a frame of reference with the x-axis parallel to the inclined plane and pointing upward (Figure 2-A). In the block acts gravitational force \( {\vec F}_{g} \), the force of friction \( {\vec F}_{f} \), and the normal reaction force \( \vec{N} \).

Figure 2

The gravitational force can be decomposed into two components, one component parallel to the x-axis \( {\vec F}_{gP} \) and the normal or perpendicular component \( {\vec F}_{gN} \) (Figure 2-B).
In the triangle on the left the gravitational force \( {\vec F}_{g} \) is perpendicular to the horizontal plane, makes an angle of 90°, the angle between the inclined plane and the horizontal plane is given as 45°, as the sum of the interior angles of a triangle equals to 180°, the angle α between the gravitational force \( {\vec{F}}_{g} \) and the parallel component \( {\vec{F}}_{gP} \) will be

\[ 45°+90°+\alpha=180°\Rightarrow \alpha=180°-45°-90°\Rightarrow \alpha=45° \]

In the triangle on the right, the normal component of gravitational force \( {\vec F}_{gN} \) makes with the inclined plane an angle of 90°, then the angle β between the gravitational force \( {\vec{F}}_{g} \) and the normal component \( {\vec{F}}_{gN} \) will be

\[ \alpha +\beta=90°\Rightarrow \beta=90°-45°\Rightarrow \beta=60° \]

they are complementary angles.
Drawing the forces in a coordinate system (Figure 2-C), we apply Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec{F}=m\vec{a}} \tag{I} \end{gather} \]

In the y direction, there is no motion the normal reaction force \( \vec{N} \) and normal component of gravitational force \( {\vec{F}}_{gN} \) cancel out

\[ \begin{gather} N=P_{N} \tag{II} \end{gather} \]

the normal component of gravitational force is given by

\[ \begin{gather} F_{gN}=F_{g}\cos 45° \tag{III} \end{gather} \]

the gravitational force is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{g}=mg} \tag{IV} \end{gather} \]

substituting the expression (IV) into expression (III)

\[ \begin{gather} F_{gN}=mg\cos 45° \tag{V} \end{gather} \]

substituting the expression (V) into expression (II)

\[ \begin{gather} N=mg\cos 45° \tag{VI} \end{gather} \]

In the x direction, we apply the expression (I) to find the acceleration of the block rising a_U

\[ \begin{gather} -F_{f}-F_{gP}=ma_{U} \tag{VII} \end{gather} \]

the force of friction is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{g}=\mu N} \tag{VIII} \end{gather} \]

substituting the expression (VI) into expression (VIII)

\[ \begin{gather} F_{f}=\mu mg\cos 45° \tag{IX} \end{gather} \]

the parallel component of the gravitational force is given by

\[ \begin{gather} F_{gP}=F_{g}\sin 45° \tag{X} \end{gather} \]

substituting the expression (IV) into expression (X)

\[ \begin{gather} F_{gP}=mg\cos 45° \tag{XI} \end{gather} \]

substituting the expressions (IX) and (XI) into expression (VII)

\[ -\mu \cancel{m}g\cos 45°-\cancel{m}g\cos 45°=\cancel{m}a_{S} \]

From the Trigonometry

\[ \sin 45°=\cos 45°=\dfrac{\sqrt{2\;}}{2} \]

\[ \begin{gather} -\mu g\frac{\sqrt{2\;}}{2}-g\frac{\sqrt{2\;}}{2}=a_{U}\\ a_{U}=-{\frac{\sqrt{2\;}}{2}}g(\mu +1) \tag{XII} \end{gather} \]

Body descending:

We choose a frame of reference with the x-axis parallel to the inclined plane and direction downward. In the block act the same forces, only the force of friction \( {\vec{F}}_{f} \) it is in the opposite direction (Figure 3-A).
Likewise, the gravitational force can be projected into two components (Figure 2-B).
We draw the forces in a coordinate system (Figure 3-B).
In y direction is valid the same expression (VI), previously found.

Figure 3

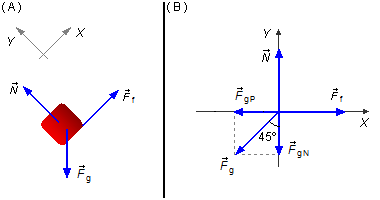
In the x direction, we apply the expression (I)

\[ \begin{gather} -F_{f}+F_{gP}=ma_{D} \tag{XIII} \end{gather} \]

substituting expressions (IX) and (XI) into expression (XIII)

\[ \begin{gather} -\mu \cancel{m}g\cos 45°+\cancel{m}g\cos 45°=\cancel{m}a_{D}\\ -\mu g\frac{\sqrt{2\;}}{2}+g\frac{\sqrt{2\;}}{2}=a_{D}\\ a_{D}=\frac{\sqrt{2\;}}{2}g(1-\mu) \tag{XIV} \end{gather} \]

From Kinematics, we have the velocity as a function of time

\[ \bbox[#99CCFF,10px] {v=v_{0}+at} \]

For the block rising, the final speed is zero, v_U = 0, and substituting the expression (XII)

\[ \begin{gather} v_{U}=v_{0U}+a_{U}t_{U}\\ 0=v_{0U}-{\frac{\sqrt{2\;}}{2}}g(\mu +1)t_{U}\\ v_{0U}=\frac{\sqrt{2\;}}{2}g(\mu +1)t_{U} \tag{XV} \end{gather} \]

For the block descending, the initial speed is zero, v_0D = 0, and substituting the expression (XIV)

\[ \begin{gather} v_{D}=v_{0D}+a_{D}t_{D}\\ v_{D}=0+\frac{\sqrt{2\;}}{2}g(1-\mu)t_{D}\\ v_{D}=\frac{\sqrt{2\;}}{2}g(1-\mu)t_{D} \tag{XVI} \end{gather} \]

Dividing the expression (XV) by (XVI)

\[ \begin{gather} \frac{v_{0U}}{v_{D}}=\frac{\dfrac{\cancel{\sqrt{2\;}}}{\cancel{2}}\cancel{g}(\mu +1)t_{U}}{\dfrac{\cancel{\sqrt{2\;}}}{\cancel{2}}\cancel{g}(1-\mu)t_{D}}\\ \frac{v_{0U}}{v_{D}}=\frac{(\mu +1)t_{U}}{(1-\mu)t_{D}} \tag{XVII} \end{gather} \]

To find the speeds, we use the equation of velocity as a function of displacement

\[ \bbox[#99CCFF,10px] {v^{2}=v_{0}^{2}+2a\Delta S} \]

The distance traveled by the block is the same on the climb and descent.
During the climb, substituting the expression (XII)

\[ \begin{gather} v_{U}^{2}=v_{0U}^{2}+2a_{U}\Delta S\\ 0^{2}=v_{0U}^{2}-\cancel{2}{\frac{\sqrt{2\;}}{\cancel{2}}}g(\mu +1)\Delta S\\ v_{0U}^{2}=\sqrt{2\;}g(\mu +1)\Delta S \\ v_{0U}=\sqrt{\sqrt{2\;}g(\mu +1)\Delta S\;} \tag{XVIII} \end{gather} \]

During the descent, substituting the expression (XIV)

\[ \begin{gather} v_{D}^{2}=v_{0D}^{2}+2a_{D}\Delta S\\ v_{D}^{2}=0^{2}+\cancel{2}\frac{\sqrt{2\;}}{\cancel{2}}g(1-\mu)\Delta S\\ v_{D}^{2}=\sqrt{2\;}g(1-\mu)\Delta S\\ v_{D}=\sqrt{\sqrt{2\;}g(1-\mu)\Delta S\;} \tag{XIX} \end{gather} \]

Substituting expressions (XVIII) and (XIX) into expression (XVII)

\[ \begin{gather} \frac{\sqrt{\sqrt{2\;}g(\mu +1)\Delta S\;}}{\sqrt{\sqrt{2\;}g(1-\mu)\Delta S\;}}=\frac{(\mu +1)t_{U}}{(1-\mu)t_{D}} \end{gather} \]

squaring both sides of the equation

\[ \begin{gather} \left(\frac{\sqrt{\sqrt{2\;}g(\mu +1)\Delta S\;}}{\sqrt{\sqrt{2\;}g(1-\mu)\Delta S\;}}\right)^{2}=\left(\frac{(\mu +1)t_{U}}{(1-\mu)t_{D}}\right)^{2}\\ \frac{\cancel{\sqrt{2\;}}\cancel{g}\cancel{(\mu +1)}\cancel{\Delta S}}{\cancel{\sqrt{2\;}}\cancel{g}\cancel{(1-\mu)}\cancel{\Delta S}}=\frac{(\mu +1)^{\cancel{2}}t_{U}^{2}}{(1-\mu)^{\cancel{2}}t_{D}^{2}}\\ 1=\frac{(\mu +1)t_{S}^{2}}{(1-\mu)t_{D}^{2}} \end{gather} \]

\[ \left(\frac{t_{S}}{t_{D}}\right)^{2}=\frac{1-\mu}{(\mu +1)} \]

substituting the value of μ given in the problem

\[ \begin{gather} \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{1-(2-\sqrt{3\;})}{2-\sqrt{3}+1}\\[5pt] \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{1-2+\sqrt{3\;}}{3-\sqrt{3\;}}\\[5pt] \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{-1+\sqrt{3\;}}{3-\sqrt{3\;}} \end{gather} \]

to rationalize this expression, we multiply the numerator and the denominator by \( 3+\sqrt{3\;} \)

\[ \begin{gather} \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{-1+\sqrt{3\;}}{3-\sqrt{3\;}}\times\frac{3+\sqrt{3\;}}{3+\sqrt{3\;}}\\[5pt] \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{-3-\sqrt{3\;}+3\sqrt{3\;}+3}{9+3\sqrt{3\;}-3\sqrt{3\;}-3}\\[5pt] \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{2\sqrt{3\;}}{6}\\[5pt] \left(\frac{t_{U}}{t_{D}}\right)^{2}=\frac{\sqrt{3\;}}{3} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {\frac{t_{U}}{t_{D}}=\sqrt{\frac{\sqrt{3\;}}{3}}} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .