Solved Problem on Harmonic Oscillations

A sledgehammer consists of a handle of mass 0.6 kg and 70 cm in length and a head of 3 kg and 6 cm in width. Calculate the moment of inertia and period of oscillations of this tool as it swings around a point at the upper end of the handle. Assume g = 9.8 m/s² for the acceleration due to gravity.

Problem data:

Handle mass: m = 0.6 kg;
Handle length: d = 70 cm;
Head mass: M = 3 kg;
Head width: D = 6 cm.

Solution

First, we must convert the dimensions of the handle and head of the sledgehammer, given in centimeters (cm), to meters (m) used in the International System of Units (S.I.)

\[ \begin{gather} d=70\;\cancel{\text{cm}}\times\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0.7\;\text{m}\\[5pt] D=6\;\cancel{\text{cm}}\times\frac{1\;\text{m}}{100\;\cancel{\text{cm}}}=0.06\;\text{m} \end{gather} \]

Moment of inertia of the handle

The moment of inertia of a bar perpendicular to the axis of rotation passing through the end of the bar is given by (Figure 1)

\[ \begin{gather} \bbox[#99CCFF,10px] {I=\int r^{2}\;dm} \tag{I} \end{gather} \]

Using the expression for the linear mass density, we obtain the mass element dm

\[ \bbox[#99CCFF,10px] {\lambda =\frac{dm}{dr}} \]

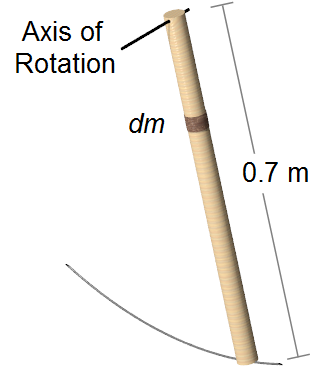
Figure 1

\[ \begin{gather} dm=\lambda \;dr \tag{II} \end{gather} \]

substituting expression (II) into expression (I)

\[ I=\int r^{2}\lambda \;dr \]

the linear density of the handle λ is constant and can be moved out of the integral, the integration is done from 0 to d in dr

\[ I=\lambda \int_{0}^{d}{r^{2}\;dr} \]

Integration of \( \displaystyle \int_{0}^{d}{r^{2}\;dr} \)

\[ \int_{0}^{d}{r^{2}\;dr}=\left.\frac{r^{2+1}}{2+1}\right|_{0}^{d}=\left.\frac{r^{3}}{3}\right|_{0}^{d}=\frac{d^{3}}{3}-\frac{0^{3}}{3}=\frac{d^{3}}{3} \]

\[ \begin{gather} I=\lambda \frac{d^{3}}{3}\\ I=\lambda d\frac{d^{2}}{3} \end{gather} \]

the term λd is the mass m of the handle, and the moment of inertia will be

\[ \begin{gather} I=\frac{1}{3}md^{2} \tag{III} \end{gather} \]

Moment of inertia of the sledgehammer head

Considering the sledgehammer head as a point mass with all mass concentrated at the center of mass. The sledgehammer head is 6 cm wide, and the center of mass is in the center 3 cm = 0.03 m from the edge. The position of the center of mass relative to the axis of rotation will be the sum of the length of the handle plus the position of the center of mass of the sledgehammer head, L = 0.7+0.03 = 0.73 m (Figure 2).
The moment of inertia of a point mass is given by

\[ \bbox[#99CCFF,10px] {I=mr^{2}} \]

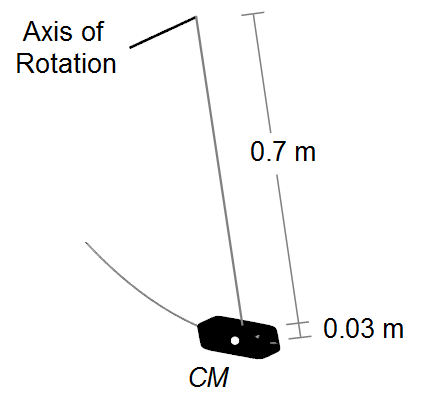
Figure 2

\[ \begin{gather} I=ML^{2} \tag{IV} \end{gather} \]

The moment of inertia of the hammer will be

\[ \begin{gather} I=\frac{1}{3}md^{2}+ML^{2}\\ I=\frac{1}{3}\times 0.6\times 0.7^{2}+3\times 0.73^{2}\\ I=0.098+1.599 \end{gather} \]

\[ \bbox[#FFCCCC,10px] {I=1.697\;\text{kg.m}^{2}} \]

The period of oscillations is given by

\[ \bbox[#99CCFF,10px] {T=2\pi \sqrt{\frac{I}{mgr}}} \]

where I is the moment of inertia found above, m is the total mass of the system, m_T, and r is the position of the system's center of mass, r_CM. The total mass is given by

\[ \begin{gather} m_{T}=m+M\\ m_{T}=0.6+3\\ m_{T}=3.6\;\text{kg} \tag{V} \end{gather} \]

Position of the center of mass of the sledgehammer

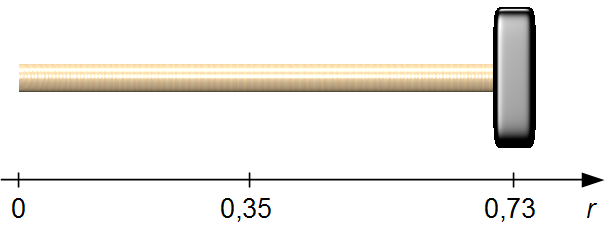
We choose a frame of reference with origin in the handle of the sledgehammer and oriented to the right. The center of mass of the handle is in the middle of the handle, \( r_{1}=\frac{d}{2}=\frac{0.7}{2}=0.35\;\text{m} \), and the head's center of mass is in the middle of the head plus the length of the handle, \( r_{2}=\frac{D}{2}+d=\frac{0.06}{2}+0.7=0.73\;\text{m} \) (Figure 3).

Figure 3

The position of the center of mass is given by

\[ \bbox[#99CCFF,10px] {r_{CM}=\frac{m_{1}r_{1}+m_{2}r_{2}}{m_{1}+m_{2}}} \]

\[ \begin{gather} r_{CM}=\frac{mr_{1}+Mr_{2}}{m+M}\\[5pt] r_{CM}=\frac{0.6\times 0.35+3\times 0.73}{0.6+3}\\[5pt] r_{CM}=\frac{2.4}{3.6}\\[5pt] r_{CM}\approx0.67\;\text{m} \end{gather} \]

The period of oscillations will be

\[ \begin{gather} T=2\times 3.14\sqrt{\frac{1.697}{3.6\times 9.8\times 0.67}}\\ T=6.28\sqrt{\frac{1.697}{23.64}} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {T=1.68\;\text{s}} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .