Solved Problem on Black Body Radiation
Português
English
advertisement
A cavity radiator at 6000 K has a 0.10 mm diameter hole drilled into its wall. Find the power radiated through the hole in the wavelength range from 5500 Å to 5510 Å.
Problem data:
- Cavity temperature: T = 6000 K;
- Hole diameter: d = 0.10 mm;
- Minimum wavelength: λ1 = 5500 Å;
- Maximum wavelength: λ2 = 5510 Å.
- Speed of light: c = 2.998 ×108 m/s;
- Planck Constant:: h = 6.63 ×10--34 J.s;
- Boltzmann Constant:: k = 1.38 ×10--23 J/K.
a) The total radiance is defined as the radiated power per unit area
\[
\begin{gathered}
R_{T}=\frac{P}{A}
\end{gathered}
\]
the integral of the radiance over all frequencies gives the radiated power
\[
\begin{gather}
P=A\int {}R_{T}(\nu)\;d\nu \tag{I}
\end{gather}
\]
The relationship between spectral radiance and energy density is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{T}(\nu)=\frac{c}{4}\rho (\nu)} \tag{II}
\end{gather}
\]
substituting expression (II) into expression (I) and integrating it into the frequency interval of the
problem
\[
\begin{gather}
P=A\int_{\nu_{1}}^{\nu_{2}}{}\frac{c}{4}\rho (\nu)\;d\nu \\[5pt]
P=\frac{Ac}{4}\int_{\nu_{1}}^{\nu_{2}}{}\rho (\nu)\;d\nu \tag{III}
\end{gather}
\]
Planck's Radiation Law for energy density is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\rho (\nu)\;d\nu =\frac{8\pi \nu^{3}}{c^{3}}\frac{h}{\operatorname{e}^{h\nu/{kT}}-1}\;d\nu} \tag{IV}
\end{gather}
\]
substituting expression (IV) in expression (III)
\[
\begin{gathered}
P=\frac{Ac}{4}\int_{\nu_{1}}^{\nu_{2}}{}\frac{8\pi \nu ^{3}}{c^{3}}\frac{h}{\operatorname{e}^{h\nu/{kT}}-1}\;d\nu \\[5pt]
P=\frac{2A\pi h}{c^{2}}\int_{\nu_{1}}^{\nu_{2}}{}\frac{\nu ^{3}}{\operatorname{e}^{h\nu/{kT}}-1}\;d\nu
\end{gathered}
\]
Note: We don't need to calculate the integral, we can approximate the value using the
Mean Value Theorem for Integrals.
The integral of a function f(x) in an interval [a, b] represents the area under the curve (Figure 1), by the Mean Value Theorem for Integrals we have a value f(c) of the function that determines a rectangle based on equal to the length of the gap and height f(c) (Figure 2).
Figure 1
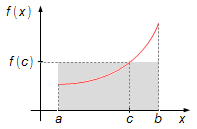Figure 2
Point c is located anywhere in the interval [a, b], such that the value
f(c) gives us equal areas under the curves.
In particular, if the function f(x) is linear the point c is at the midpoint of the interval [a, b] (Figure 3). This happens because the areas above and below the value of f(c) compensate each other.
Figure 3
In the problem, the difference in wavelengths relative to the given values is
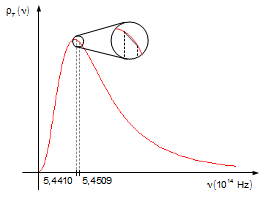Figure 4
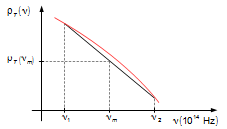Figure 5
The integral of a function f(x) in an interval [a, b] represents the area under the curve (Figure 1), by the Mean Value Theorem for Integrals we have a value f(c) of the function that determines a rectangle based on equal to the length of the gap and height f(c) (Figure 2).
In particular, if the function f(x) is linear the point c is at the midpoint of the interval [a, b] (Figure 3). This happens because the areas above and below the value of f(c) compensate each other.
In the problem, the difference in wavelengths relative to the given values is
\[
\begin{gathered}
\frac{\Delta \lambda }{\lambda _{1}}=\frac{\lambda _{2}-\lambda_{1}}{\lambda_{1}}=\frac{5510\times 10^{-10}-5500\times 10^{-10}}{5500\times 10^{-10}}=0.002
\end{gathered}
\]
\[
\begin{gathered}
\frac{\Delta \lambda }{\lambda _{2}}=\frac{\lambda _{2}-\lambda_{1}}{\lambda_{2}}=\frac{5510\times 10^{-10}-5500\times 10^{-10}}{5510\times 10^{-10}}=0.002
\end{gathered}
\]
we see that the variation in the range of wavelengths varies from 2 parts per 1000, this range is small,
as frequencies and wavelengths are related the range of frequencies in which we must integrate the
function is small (Figure 4), we can approximate the infinitesimal range of frequencies, dν, by
the range, Δν, and the integration variable, ν, can be substituted by its
average value, νm (Figure 5).
We can substitute the integral to the power with the following expression
\[
\begin{gathered}
P=\frac{2A\pi h}{c^{2}}\frac{\nu_{m}^{3}}{\operatorname{e}^{h\nu_{m}/{kT}}-1}\;\Delta \nu
\end{gathered}
\]
The frequency is given by
\[
\begin{gathered}
\bbox[#99CCFF,10px]
{\nu =\frac{c}{\lambda}}
\end{gathered}
\]
\[
\begin{gathered}
\nu_{1}=\frac{c}{\lambda _{1}}\\[5pt]
\nu_{1}=\frac{2.998\times 10^{8}}{5500\times 10^{-10}}\\[5pt]
\nu_{1}=5.4509\times 10^{14}\;\text{Hz}
\end{gathered}
\]
\[
\begin{gathered}
\nu_{2}=\frac{c}{\lambda _{2}}\\[5pt]
\nu_{2}=\frac{2.998\times 10^{8}}{5510\times 10^{-10}}\\[5pt]
\nu_{2}=5.4410\times 10^{14}\;\text{Hz}
\end{gathered}
\]
substituting the integration variable ν by the average value of the frequency range
\[
\begin{gathered}
\nu_{m}=\frac{\nu_{1}+\nu_{2}}{2}\\[5pt]
\nu_{m}=\frac{5.4509\times 10^{14}+5.4410\times 10^{14}}{2}\\[5pt]
\nu_{m}=\frac{10.8919\times 10^{14}}{2}\\[5pt]
\nu_{m}=5.446\times 10^{14}\;\text{Hz}
\end{gathered}
\]
and substituting the differential interval dν by the interval Δν given by
\[
\begin{gathered}
\Delta \nu =\nu_{1}-\nu_{2}\\[5pt]
\Delta \nu=5.4509\times 10^{14}-5.4410\times 10^{14}\\[5pt]
\Delta \nu=9.9\times 10^{11}\;\text{Hz}
\end{gathered}
\]
The area of the hole will be
\[
\begin{gathered}
A=\pi r^{2}\\
A=\pi\left(\frac{d}{2}\right)^{2}\\[5pt]
A=3.14\times \left(\frac{10\times 10^{-3}}{2}\right)^{2}\\[5pt]
A=7.85\times 10^{-5}\;\text{m}^{2}
\end{gathered}
\]
substituting the data
\[
\begin{split}
P=&\frac{2\times (7.85\times 10^{-5})\times 3.14\times (6.63\times 10^{-34})}{(2.998\times 10^{8})^{2}}\times\\
&\times \frac{(5.446\times 10^{14})^{3}}{\operatorname{e}^{(6.63\times 10^{-34})\times (5.446\times 10^{14})/{[(1.38\times 10^{-23})\times (6000)]}}-1}\times (9.9\times 10^{11})\\[5pt]
&\quad \quad P=\frac{3.27\times 10^{-37}}{8.98\times 10^{16}}\times \frac{1.62\times 10^{44}}{\operatorname{e}^{4.36}-1}\times (9.9\times 10^{11})\\[5pt]
&\quad \quad P=3.64\times 10^{-54}\times 2.09\times 10^{42}\times 9.9\times 10^{11}
\end{split}
\]
\[ \bbox[#FFCCCC,10px]
{P=7.5\;\text{W}}
\]
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .