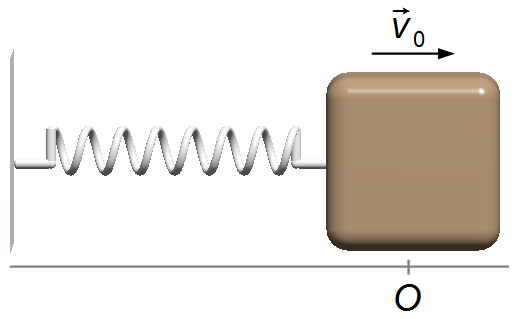
A block of mass m is attached to a spring, the spring constant is equal to k. The block is launched, from the equilibrium position O, with an initial velocity v₀. Determine:
a) The differential equation of motion;
b) The solution of the equation for the mass-spring system and the angular frequency of oscillations.

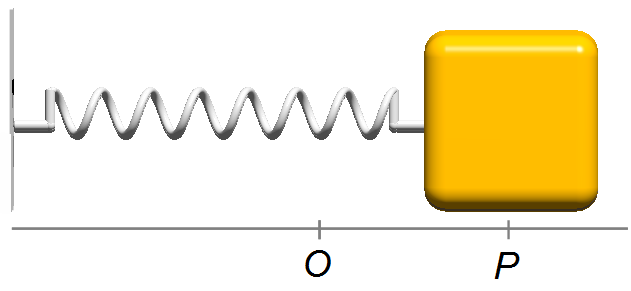
A block of mass m = 0.25 kg is connected to a spring of constant k = 1 N/m. The block is displaced from its equilibrium position O to a point P to 0.5 m and released from rest. Determine:
a) Equation of displacement as a function of time;
b) The speed of the block;
c) Calculate the mechanical energy of the oscillator; d) The graph of position x as a function of time t.

A block of mass m is attached to the end of a spring, the spring constant is equal to k, and placed on a horizontal frictionless surface. The other end of the spring is fixed at a point in the wall. The block is displaced from its equilibrium position and released. Determine:
a) The equation of motion of the block;
b) The velocity as a function of the mass, m, the spring constant, k, the amplitude, A, and the distance, x, between the block and the point of equilibrium of the spring;
c) The magnitude of the maximum speed;
d) The acceleration as a function of the mass, m, the spring constant, k, and the distance, x, between the block and the point of equilibrium of the spring;
e) The magnitude of the maximum acceleration;
f) The kinetic energy;
g) The potential energy;
h) The total energy.

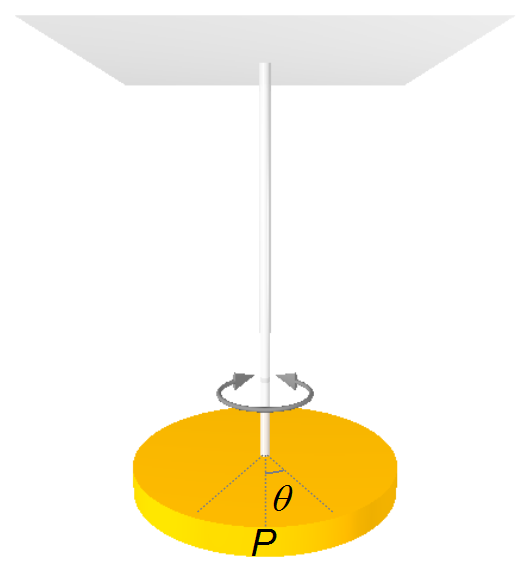
A body of mass m is suspended, by a wire of torsion constant κ, from the ceiling. The body is displaced through an angle θ₀ and released from rest. Determine:
a) The differential equation of motion;
b) The solution of the equation for the torsional pendulum and the angular frequency of oscillations;
c) The period of the oscillations.

A block of mass m is attached to a spring, the spring constant is equal to k and a shock absorber of damping coefficient b. The block is moved from its equilibrium position O to a point x₀ and released from rest. Using the damping force proportional to velocity, determine:
a) The differential equation of motion;
b) The equation solution for the system in the case of underdamped oscillations and the angular frequency of the oscillations.

A block of mass m = 2.50 kg is attached to a spring with a spring constant k = 12.00 N/m and a shock absorber with a damping coefficient b = 0.60 N.s/m. The block is displaced from its equilibrium position O to a point x₀ at 0.20 m and released from rest. Determine:
a) The equation of motion;
b) What is the type of oscillator?
c) The graph of position x versus time t.