Solved Problem on Kinematics
advertisement
A particle is on a plane xy, initially at rest in the position x0 on the positive x-axis. It begins to move with constant velocities vx, in the direction of origin, and vy in the direction of the positive y-axis. Determine after how long the particle will be at the minimum distance of the origin and, what is this minimum distance.
Problem data:
- Initial position of the particle: x0;
- Speed of the particle in direction x: vx;
- Speed of the particle in direction y: vy.
As the components of the speed are constants the trajectory will be a straight line (Figure 1-A).
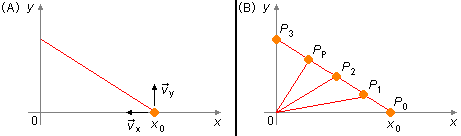
Along the trajectory, the particle passes successively by points P0, P1, P2, PP, P3, and so on. The point of minimum distance to the origin will be the point PP, where the line of this point to the origin is perpendicular to the trajectory (Figure 1-B).
Solution
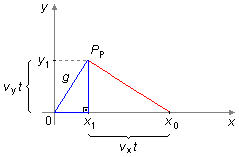
From the triangle in blue, we have that the base measures
\( x_{1}=x_{0}-v_{x}t \)
and its height
\( y_{1}=v_{y}t \),
applying the Pythagorean Theorem
To find the instant where the distance is a minimum, we must take the derivative of the expression (I) with respect to time and equal to zero.
\[
\begin{gather}
g^{2}=(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\\
g=[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}]^{\frac{1}{2}} \tag{I}
\end{gather}
\]
so we have the distance of the point with the smallest distance from the origin as the function of
time.To find the instant where the distance is a minimum, we must take the derivative of the expression (I) with respect to time and equal to zero.
Differentiation of \( g=[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}]^{\frac{1}{2}} \)
The g(t) function is a composite function whose derivative is given by the rule of the chain
The g(t) function is a composite function whose derivative is given by the rule of the chain
\[
\begin{gather}
\frac{dg[h(t)]}{dt}=\frac{dg}{dh}\;\frac{dh}{dt} \tag{II}
\end{gather}
\]
with
\( g(h)=h^{\frac{\;1}{2}} \)
and
\( h(t)=(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2} \)
\[
\begin{align}
&\frac{dg}{dh}=\frac{1}{2}h^{\frac{1}{2}-1}=\frac{1}{2}h^{\frac{1-2}{2}}=\frac{1}{2}h^{-{\frac{1}{2}}}=\frac{1}{2}\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{-{\frac{1}{2}}} \tag{III}\\[5pt]
&\frac{dh}{dt}=\frac{d}{dt}\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right] \tag{IV}
\end{align}
\]
substituting expressions (III) and (IV) into expression (II)
\[
\begin{gather}
\frac{dg[h(t)]}{dt}=\frac{1}{2}\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{-{\frac{1}{2}}}\;\frac{d}{dt}\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right] \tag{V}
\end{gather}
\]
the derivative of the sum is the sum of derivatives
\[
\begin{gather}
\frac{dh}{dt}=\frac{d}{dt}(x_{0}-v_{x}t)^{2}+\frac{d}{dt}(v_{y}t)^{2} \tag{VI}
\end{gather}
\]
substituting the expression (VI) into (V)
\[
\begin{gather}
\frac{dg[h(t)]}{dt}=\frac{1}{2}\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{-{\frac{1}{2}}}\;\left[\frac{d}{dt}(x_{0}-v_{x}t)^{2}+\frac{d}{dt}(v_{y}t)^{2}\right] \tag{VII}
\end{gather}
\]
the first function in parentheses is a composite function whose derivative is given by the chain rule
\[
\begin{gather}
\frac{df[w(t)]}{dt}=\frac{df}{dv}\;\frac{dw}{dt} \tag{VIII}
\end{gather}
\]
applying the expression (VIII) to the term
\( (x_{0}-v_{x}t)^{2} \)
of the expression (VII), with
\( f(w)=w^{2} \)
and
\( w(t)=x_{0}-v_{x}t \),
the derivatives will be
\[
\begin{align}
&\frac{df}{dw}=2w^{2-1}=2w \tag{IX}\\[5pt]
&\frac{dw}{dt}=0-v_{x}t^{1-1}=-v_{x} \tag{X}
\end{align}
\]
substituting expressions (IX) and (X) into expression (VIII)
\[
\begin{gather}
\frac{df[v(t)]}{dt}=-2(x_{0}-v_{x}t)v_{x} \tag{XI}
\end{gather}
\]
the derivative of therm
\( (v_{x}t)^{2} \)
is
\[
\begin{gather}
\frac{d}{dt}(v_{y}t)^{2}=\frac{d}{dt}(v_{y}^{2}t^{2})=2v_{y}^{2}t \tag{XII}
\end{gather}
\]
Substituting expressions (XI) and (XII) into expression (VII)
\[
\begin{gather}
\frac{dg}{dt}=\frac{1}{2}\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{-{\frac{1}{2}}}\;\left[-2(x_{0}-v_{x}t)v_{x}+2v_{y}^{2}t\right]\\[5pt]
\frac{dg}{dt}=\frac{1}{2}\frac{\left[-2(x_{0}-v_{x}t)v_{x}+2v_{y}^{2}t\right]}{\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{\frac{1}{2}}}\\[5pt]
\frac{dg}{dt}=\frac{-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t}{\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{\frac{1}{2}}} \tag{XIII}
\end{gather}
\]
With the condition that the derivative should be zero \( \left(\dfrac{dg}{dt}=0\right) \), we have in the expression (XIII)
\[
\begin{gather}
\frac{-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t}{\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{\frac{1}{2}}}=0\\
-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t=0.\left[(x_{0}-v_{x}t)^{2}+(v_{y}t)^{2}\right]^{\frac{1}{2}}\\
-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t=0\\t(v_{x}^{2}+v_{y}^{2})=x_{0}v_{x}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}}
\]
Substituting this value in the expression (I), we have the minimum distance from the furniture to the origin
\[
\begin{gather}
g=\sqrt{\left(x_{0}-v_{x}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(v_{y}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt]
g=\sqrt{\left(\frac{x_{0}(v_{x}^{2}+v_{y}^{2})-x_{0}v_{x}^{2}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(\frac{x_{0}v_{x}v_{y}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt]
g=\sqrt{\left(\frac{{x}_{0}v_{y}^{2}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(\frac{x_{0}v_{x}{v}_{y}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt]
g=\sqrt{\frac{{x}_{0}^{2}v_{y}^{4}+x_{0}^{2}v_{x}^{2}v_{y}^{2}}{(v_{x}^{2}+v_{y}^{2})^{2}}\;}\\[5pt]
g=\sqrt{\frac{{x}_{0}^{2}v_{y}^{2}(v_{y}^{2}+v_{y}^{2})}{(v_{x}^{2}+v_{y}^{2})^{2}}\;}\\[5pt]
g=\sqrt{\frac{{x}_{0}^{2}v_{y}^{2}}{v_{x}^{2}+v_{y}^{2}}\;}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{g=\frac{{x}_{0}v_{y}}{\sqrt{v_{x}^{2}+v_{y}^{2}\;}}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .