Solved Problem on Dynamics

A particle of mass m is released at rest and falls under the action of the force of gravity, and force of resistance proportional to falling speed. Determine:
a) The equation of velocity as a function of time;
b) The terminal velocity;
c) The equation of displacement as a function of time;
d) The acceleration of motion.

Problem data:

Mass of the particle: m;
Initial speed of the particle: v₀ = 0;
Drag coefficient: b.

Problem diagram:

We choose a reference frame pointing downward with origin at the point where the particle is released. In the particle acts the gravitational force F_g in the direction of the fall and the drag force F_d in the opposite direction of motion.

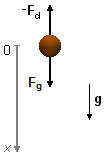
Figure 1

Solution

a) Applying Newton's Second Law

\[ \bbox[#99CCFF,10px] {{\mathbf F}=m\mathbf{\dot v}} \]

\[ {\mathbf F}_{g}-{\mathbf F}_{d}=m\mathbf{\dot v} \]

the gravitational force is given by

\[ \bbox[#99CCFF,10px] {{\mathbf F}_{g}=m{\mathbf g}} \]

and drag force is given by

\[ \bbox[#99CCFF,10px] {{\mathbf F}_{d}=b{\mathbf v}} \]

substituting these expressions

\[ mg\;{\mathbf j}-bv\;{\mathbf j}=m {\dot v}\;{\mathbf j} \]

as there is motion only in one dimension, we have magnitude

\[ mg-bv=m {\dot v} \]

writing \( {\dot v}=\frac{dv}{dt} \) and separating the variables

\[ \begin{gather} mg-bv=m\frac{dv}{dt}\\ m\frac{dv}{dt}=b\left(\frac{mg}{b}-v\right)\\ \frac{dv}{\left(\dfrac{mg}{b}-v\right)}=\frac{b}{m}dt \end{gather} \]

integrating the left-hand side from 0 to v(t), the speed at any instant t any, and on the right-hand side integrating the time from 0 to t, any instant t

\[ \begin{gather} \int_{0}^{{v(t)}}{\frac{dv}{\left(\dfrac{mg}{b}-v\right)}}=\int_{0}^{t}{\frac{b}{m}dt}\\ \int_{0}^{{v(t)}}{\frac{dv}{\left(\dfrac{mg}{b}-v\right)}}=\frac{b}{m}\int_{0}^{t}{dt} \end{gather} \]

Integration of \( \displaystyle \int_{0}^{{v(t)}}{\dfrac{dv}{\left(\dfrac{mg}{b}-v\right)}} \)

Changing the variable

\[ \begin{array}{l} u=\dfrac{mg}{b}-v\\ \dfrac{du}{dv}=-1\Rightarrow dv=-du \end{array} \]

changing the limits of integration

for    \( v=0 \)
we have    \( u=\dfrac{mg}{b} \)

for    \( v=v(t) \)
we have    \( u=\dfrac{mg}{b}-v(t) \)

substituting in the integral

\[ \begin{split} \int_{{\frac{mg}{b}}}^{{\frac{mg}{b}-v(t)}}{\frac{-du}{u}} &=-\left[\left.\ln u\;\right|_{\;\frac{mg}{b}}^{\;\frac{mg}{b}-v(t)}\right]=-\left[\ln\left(\frac{mg}{b}-v(t)\right)-\ln\left(\frac{mg}{b}\right)\right]=\\ &=-\ln\left(\frac{\dfrac{mg}{b}-v(t)}{\dfrac{mg}{b}}\right)=-\ln\left(\frac{\dfrac{mg-bv(t)}{\cancel{b}}}{\dfrac{mg}{\cancel{b}}}\right)=\\ &=-\ln\left(\frac{mg-bv(t)}{mg}\right) \end{split} \]

Integration of \( \displaystyle \int_{0}^{t}{dt'} \)

\[ \int_{0}^{t}{dt'}=\left.t'\;\right|_{\;0}^{\;t}=t-0=t \]

\[ \begin{gather} -\ln\left(\frac{mg-bv(t)}{mg}\right)=\frac{b}{m}t\\[5pt] \ln\left(\frac{mg-bv(t)}{mg}\right)=-{\frac{b}{m}}t\\[5pt] \frac{mg-bv(t)}{mg}=\operatorname{e}^{-{\frac{b}{m}}t}\\[5pt] mg-bv(t)=mg\operatorname{e}^{-{\frac{b}{m}}t}\\[5pt] bv(t)=mg-mg\operatorname{e}^{-{\frac{b}{m}}t}\\[5pt] bv(t)=mg\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right) \end{gather} \]

\[ \bbox[#FFCCCC,10px] {v(t)=\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)} \]

b) The terminal velocity will be found by calculating the limit of the expression of speed when \( t\rightarrow \infty \)

\[ \begin{split} v_{T}=\underset{t\rightarrow \infty }{\lim}v(t) &=\underset{t\rightarrow \infty }{\lim}{\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)}=\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}\infty}\right)=\\[5pt] &=\frac{mg}{b}\left(1-\operatorname{e}^{-\infty}\right)=\frac{mg}{b}\left(1-\frac{1}{\operatorname{e}^{\infty}}\right)=\\[5pt] &=\frac{mg}{b}\left(1-\frac{1}{\infty}\right)=\frac{mg}{b}\left(1-0\right) \end{split} \]

\[ \bbox[#FFCCCC,10px] {v_{T}=\frac{mg}{b}} \]

c) Substituting \( v=\dfrac{dx}{dt} \), the equation of speed can be written as

\[ \begin{gather} \frac{dx}{dt}=\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)\\[5pt] dx=\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)dt \end{gather} \]

integrating the left-hand side from 0 to x(t), the position at any instant t, and on the right-hand side integrating the time from 0 to t, any instant t

\[ \begin{gather} \int _{0}^{{x(t)}}{dx}=\int_{0}^{t}{\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}t}}\right)dt}\\[5pt] \int_{0}^{{x(t)}}{dx}=\frac{mg}{b}\left(\int _{0}^{t}dt-\int_{0}^{t}\operatorname{e}^{-{\frac{b}{m}t}}dt\right) \end{gather} \]

Integration of \( \displaystyle \int_{0}^{{x(t)}}{dx} \)

\[ \int _{0}^{{x(t)}}{dx}=\left.x\;\right|_{\;0}^{\;x(t)}=x(t)-0=x(t) \]

The integral \( \displaystyle \int _{0}^{t}{dt} \) has already been calculated above.

Integration of \( \displaystyle \int_{0}^{t}\operatorname{e}^{-{\frac{b}{m}t}}dt \)

Changing the variable

\[ \begin{array}{l} u=-{\dfrac{b}{m}}t\\ \dfrac{du}{dt}=-{\dfrac{b}{m}}\Rightarrow dt=-{\dfrac{m}{b}}du \end{array} \]

changing the limits of integration

for    \( t=0 \)
we have    \( u=-{\dfrac{b}{m}}.0=0 \)

for    \( t=t \)
we have    \( u=-{\dfrac{b}{m}}t \)

\[ \begin{split} \int_{0}^{{-{\frac{b}{m}}t}}-{\frac{m}{b}}\operatorname{e}^{u}du &=-\frac{m}{b}\int_{0}^{{-{\frac{b}{m}}t}}\operatorname{e}^{u}du\Rightarrow-\frac{m}{b}\left(\left.\operatorname{e}^{u}\;\right|_{\;0}^{\;-\frac{b}{m}t}\right)\Rightarrow\\[5pt] &\Rightarrow -\frac{m}{b}\left(\operatorname{e}^{-{\frac{b}{m}}t}-\operatorname{e}^{0}\right)\Rightarrow-\frac{m}{b}\left(\operatorname{e}^{-{\frac{b}{m}}t}-1\right)=\\[5pt] &=\frac{m}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right) \end{split} \]

\[ x(t)=\frac{mg}{b}\left[t-\frac{m}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)\right] \]

\[ \bbox[#FFCCCC,10px] {x(t)=\frac{mg}{b}\left[t+\frac{m}{b}\left(\operatorname{e}^{-{\frac{b}{m}}t}-1\right)\right]} \]

d) The acceleration is found by differentiating the equation of velocity \( a=\frac{dv}{dt} \)

\[ \begin{gather} a(t)=\frac{d}{dt}\left[\frac{mg}{b}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)\right]\\[5pt] a(t)=\frac{mg}{b}\frac{d}{dt}\left(1-\operatorname{e}^{-{\frac{b}{m}}t}\right)\\[5pt] a(t)=\frac{mg}{b}\left[0-\left(-{\frac{b}{m}}\right)\operatorname{e}^{-{\frac{b}{m}}t}\right]\\[5pt] a(t)=\frac{\cancel{m}g}{\cancel{b}}\frac{\cancel{b}}{\cancel{m}}\operatorname{e}^{-{\frac{b}{m}}t} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {a(t)=g\operatorname{e}^{-{\frac{b}{m}}t}} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .