Solved Problem on Coulomb's Law and Electric Field
Português
English
advertisement
A hemispherical bowl of radius a carries a uniformly distributed charged Q. Calculate the
electric field vector at a point P in the center of the hemisphere base.
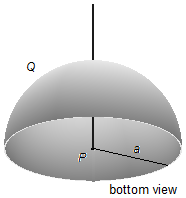
Problem data:
- Radius of the hemispherical bowl: a;
- Charge of the hemispherical bowl: Q.
The position vector r goes from an element of charge dq to point P where we want to calculate the electric field, the vector rq locates the charge element relative to the origin of the reference frame, and the vector rp locates point P (Figure 1).
\[
\begin{gather}
\mathbf{r}=\mathbf{r}_{p}-\mathbf{r}_{q}
\end{gather}
\]
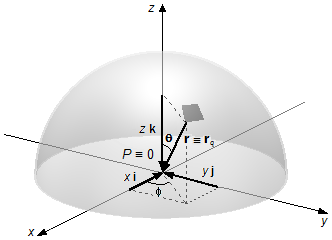
From the geometry of the problem, we choose spherical coordinates, lies at the origem and its distnace is equal to zero \( \mathbf{r}_{p}=\mathbf{0} \), and the vector rq, match with the vector r, is written as \( \mathbf{r}_{q}=x\;\mathbf{i}+y\;\mathbf{j}+z\;\mathbf{k} \), the position vector will be
\[
\begin{gather}
\mathbf{r}=\mathbf{0}-(x\;\mathbf{i}+y\;\mathbf{j}+z\;\mathbf{k})\\[5pt]
\mathbf{r}=-x\;\mathbf{i}-y\;\mathbf{j}-z\;\mathbf{k} \tag{I}
\end{gather}
\]
From expression (I), the magnitude of the position vector r will be
\[
\begin{gather}
r^{2}=(-x)^{2}+(-y)^{2}+(-z)^{2}\\[5pt]
r=\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
where x, y, and z, in spherical coordinates, are given by
\[
\left\{
\begin{array}{l}
x=a\sin \theta \cos \phi \\[5pt]
y=a\sin \theta \sin \phi \\[5pt]
z=a\cos \theta
\end{array}
\right. \tag{III}
\]
Solution
The electric field vector is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\end{gather}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{IV}
\end{gather}
\]
Using the expression of the surface density of charge σ, we have the charge element dq
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sigma =\frac{dq}{dA}}
\end{gather}
\]
\[
\begin{gather}
dq=\sigma \;dA \tag{V}
\end{gather}
\]
where dA is an element of area of the hemisphere.To obtain the element of area in spherical coordinates, we calculate the Jacobian given by the determinant
\[
\begin{gather}
J=\left|
\begin{matrix}
\;\dfrac{\partial x}{\partial r}&\dfrac{\partial x}{\partial \theta}&\dfrac{\partial x}{\partial \phi}\;\\
\;\dfrac{\partial y}{\partial r}&\dfrac{\partial y}{\partial \theta}&\dfrac{\partial y}{\partial \phi}\;\\
\;\dfrac{\partial z}{\partial r}&\dfrac{\partial z}{\partial \theta}&\dfrac{\partial z}{\partial \phi}\;
\end{matrix}\right|
\end{gather}
\]
Calculation of partial derivatives of functions x, y, and z given in (III)
\( x=r\sin \theta \cos \phi \):
\( \dfrac{\partial x}{\partial r}=\dfrac{\partial (r\sin \theta\cos \phi)}{\partial r}=\sin \theta \cos \phi\dfrac{\partial r}{\partial r}=\sin \theta \cos \phi .1=\sin \theta \cos \phi \text{, }\)
\( \dfrac{\partial x}{\partial \theta}=\dfrac{\partial(r\sin \theta \cos \phi)}{\partial \theta}=r\cos \phi\dfrac{\partial (\sin \theta \;)}{\partial \theta}=r\cos\theta \cos \phi \text{, } \)
\( \dfrac{\partial x}{\partial \phi }=\dfrac{\partial(r\sin \theta \cos \phi)}{\partial \phi}=r\sin \theta \dfrac{\partial (\cos \phi)}{\partial \phi}=r\sin \theta (-\sin \phi)=-r\sin \theta \sin \phi \text{, } \)
\( y=r\sin \theta \sin \phi \):
\( \dfrac{\partial y}{\partial r}=\dfrac{\partial (r\sin \theta\sin \phi)}{\partial r}=\sin \theta\sin \phi \dfrac{\partial r}{\partial r}=\sin \theta \sin \phi.1=\sin \theta \sin \phi \text{, } \)
\( \dfrac{\partial y}{\partial \theta}=\dfrac{\partial(r\sin \theta \sin \phi)}{\partial \theta}=r\sin \phi \dfrac{\partial (\sin \theta)}{\partial \theta}=r\cos \theta \sin \phi \text{, } \)
\( \dfrac{\partial y}{\partial \phi}=\dfrac{\partial(r\sin \theta \sin \phi)}{\partial \phi}=r\sin \theta \dfrac{\partial (\sin \phi)}{\partial \phi }=r\sin \theta \cos \phi \text{, } \)
\( z=r\cos \theta \):
\( \dfrac{\partial z}{\partial r}=\dfrac{\partial (r\cos \theta )}{\partial r}=\cos \theta \dfrac{\partial r}{\partial r}=\cos \theta .1=\cos \theta \text{, } \)
\( \dfrac{\partial z}{\partial \theta}=\dfrac{\partial (r\cos \theta)}{\partial \theta}=r\dfrac{\partial (\cos \theta )}{\partial \theta}=r(-\sin \theta )=-r\sin \theta \text{, } \)
\( \dfrac{\partial z}{\partial \phi }=\dfrac{\partial (r\cos \theta)}{\partial \phi }=0 \), the function z does not depend on ϕ, in the derivative in ϕ the values of r and θ are constants and the derivative of a constant is zero.
\( x=r\sin \theta \cos \phi \):
\( \dfrac{\partial x}{\partial r}=\dfrac{\partial (r\sin \theta\cos \phi)}{\partial r}=\sin \theta \cos \phi\dfrac{\partial r}{\partial r}=\sin \theta \cos \phi .1=\sin \theta \cos \phi \text{, }\)
\[ \dfrac{\partial x}{\partial r}=\dfrac{\partial (r\sin \theta\cos \phi)}{\partial r}=\sin \theta \cos \phi\dfrac{\partial r}{\partial r}=\sin \theta \cos \phi .1=\sin \theta \cos \phi \]
In the derivative in r, the values of θ and ϕ are constants, the sine and cosine are
moved outside of the derivative.
\( \dfrac{\partial x}{\partial \theta}=\dfrac{\partial(r\sin \theta \cos \phi)}{\partial \theta}=r\cos \phi\dfrac{\partial (\sin \theta \;)}{\partial \theta}=r\cos\theta \cos \phi \text{, } \)
\[ \dfrac{\partial x}{\partial \theta}=\dfrac{\partial(r\sin \theta \cos \phi)}{\partial \theta}=r\cos \phi\dfrac{\partial (\sin \theta \;)}{\partial \theta}=r\cos\theta \cos \phi \]
In the derivative in θ, the values of r and ϕ are constants, the term in r and
the sine are moved outside of the derivative.
\( \dfrac{\partial x}{\partial \phi }=\dfrac{\partial(r\sin \theta \cos \phi)}{\partial \phi}=r\sin \theta \dfrac{\partial (\cos \phi)}{\partial \phi}=r\sin \theta (-\sin \phi)=-r\sin \theta \sin \phi \text{, } \)
\[ \dfrac{\partial x}{\partial \phi }=\dfrac{\partial(r\sin \theta \cos \phi)}{\partial \phi}=r\sin \theta \dfrac{\partial (\cos \phi)}{\partial \phi}=r\sin \theta (-\sin \phi)=-r\sin \theta \sin \phi \]
In the derivative in ϕ, the values of r and θ are constants, the term in r and
the sine are moved outside of the derivative.
\( y=r\sin \theta \sin \phi \):
\( \dfrac{\partial y}{\partial r}=\dfrac{\partial (r\sin \theta\sin \phi)}{\partial r}=\sin \theta\sin \phi \dfrac{\partial r}{\partial r}=\sin \theta \sin \phi.1=\sin \theta \sin \phi \text{, } \)
\[ \dfrac{\partial y}{\partial r}=\dfrac{\partial (r\sin \theta\sin \phi)}{\partial r}=\sin \theta\sin \phi \dfrac{\partial r}{\partial r}=\sin \theta \sin \phi.1=\sin \theta \sin \phi \]
In the derivative in r, the values θ and ϕ are constants, the terms in sine are moved
outside of the derivative.
\( \dfrac{\partial y}{\partial \theta}=\dfrac{\partial(r\sin \theta \sin \phi)}{\partial \theta}=r\sin \phi \dfrac{\partial (\sin \theta)}{\partial \theta}=r\cos \theta \sin \phi \text{, } \)
\[ \frac{\partial y}{\partial \theta}=\frac{\partial(r\sin \theta \sin \phi)}{\partial \theta}=r\sin \phi \frac{\partial (\sin \theta)}{\partial \theta}=r\cos \theta \sin \phi \]
In the derivative in θ, the values of r and ϕ are constants, the term in r and
the sine are moved outside of the derivative.
\( \dfrac{\partial y}{\partial \phi}=\dfrac{\partial(r\sin \theta \sin \phi)}{\partial \phi}=r\sin \theta \dfrac{\partial (\sin \phi)}{\partial \phi }=r\sin \theta \cos \phi \text{, } \)
\[ \dfrac{\partial y}{\partial \phi }=\dfrac{\partial(r\sin \theta \sin \phi)}{\partial \phi}=r\sin \theta \dfrac{\partial (\sin \phi)}{\partial \phi }=r\sin \theta \cos \phi \]
In the derivative in ϕ, the values of r and θ are constants, the term in r and
the sine are moved outside of the derivative.
\( z=r\cos \theta \):
\( \dfrac{\partial z}{\partial r}=\dfrac{\partial (r\cos \theta )}{\partial r}=\cos \theta \dfrac{\partial r}{\partial r}=\cos \theta .1=\cos \theta \text{, } \)
\[ \dfrac{\partial z}{\partial r}=\dfrac{\partial (r\cos \theta )}{\partial r}=\cos \theta \dfrac{\partial r}{\partial r}=\cos \theta .1=\cos \theta \]
In the derivative in r, the value of θ is constant, the term in cosine is moved outside of
the derivative.
\( \dfrac{\partial z}{\partial \theta}=\dfrac{\partial (r\cos \theta)}{\partial \theta}=r\dfrac{\partial (\cos \theta )}{\partial \theta}=r(-\sin \theta )=-r\sin \theta \text{, } \)
\[ \dfrac{\partial z}{\partial \theta}=\dfrac{\partial (r\cos \theta)}{\partial \theta}=r\dfrac{\partial (\cos \theta )}{\partial \theta}=r(-\sin \theta )=-r\sin \theta \]
In the derivative in θ, the value of r is constant, the term in r is moved outside
of the derivative.
\( \dfrac{\partial z}{\partial \phi }=\dfrac{\partial (r\cos \theta)}{\partial \phi }=0 \), the function z does not depend on ϕ, in the derivative in ϕ the values of r and θ are constants and the derivative of a constant is zero.
\[
\begin{gather}
dA=J\;d\theta \;d\phi
\end{gather}
\]
Note: There is no dr variation because the body is a hemispheric bowl of constant
radius equal to a.
\[
\begin{gather}
J=\left|
\begin{matrix}
\;\sin \theta \cos \phi & r\cos \theta\cos \phi & -r\sin \theta \sin \phi\;\\
\;\sin \theta \sin \phi & r\cos \theta\sin \phi & r\sin \theta \cos \phi \;\\
\;\cos\theta & -r\sin \theta & 0\;
\end{matrix}\right|
\end{gather}
\]
calculating the determinant by the Rule of Sarrus
\[
\begin{gather}
J=(\sin \theta \cos \phi).(r\cos \theta\sin \phi).0+(r\cos \theta \cos \phi).(r\sin \theta \cos\phi).(\cos \theta )\text{+}\\
\qquad\text{+}(-r\sin \theta \sin \phi).(\sin \theta \sin \phi).(-r\sin \theta )-(-r\sin \theta\sin \phi).(r\cos \theta \sin \phi).(\cos\theta )\text{--}\\
\text{--}(\sin \theta \cos \phi).(r\sin \theta \cos \phi).(-r\sin \theta)-(r\cos \theta \cos \phi).(\sin \theta\sin \phi).0 \qquad\quad\; \\[5pt]
J=0+r^{2}\cos ^{2}\theta\sin \theta \cos ^{2}\phi+r^{2}\sin ^{3}\theta \sin ^{2}\phi+r^{2}\cos ^{2}\theta \sin \theta\sin ^{2}\phi +r^{2}\sin ^{3}\theta \cos^{2}\phi -0\\[5pt]
J=r^{2}[\cos ^{2}\theta \sin \theta \cos^{2}\phi +\sin ^{3}\theta \sin ^{2}\phi +\cos^{2}\theta \sin \theta \sin ^{2}\phi+\sin ^{3}\theta \cos ^{2}\phi ]\\[5pt]
J=r^{2}[\cos^{2}\theta \sin \theta \underbrace{(\cos ^{2}\phi+\sin ^{2}\phi)}_{1}+\sin ^{3}\theta\underbrace{(\cos ^{2}\phi +\sin ^{2}\phi)}_{1}]\\[5pt]
J=r^{2}[\cos ^{2}\theta \sin \theta+\sin ^{2}\theta \sin \theta]\\[5pt]
J=r^{2}[\underbrace{(\cos ^{2}\theta+\sin ^{2}\theta )}_{1}\sin \theta]\\[5pt]
J=r^{2}\sin \theta
\end{gather}
\]
\[
\begin{gather}
dA=r^{2}\sin \theta \;d\theta \;d\phi \tag{VI}
\end{gather}
\]
substituting the expression (VI) into expression (V)
\[
\begin{gather}
dq=\sigma r^{2}\sin \theta \;d\theta \;d\phi \tag{VII}
\end{gather}
\]
Substituting expressions (VII) into expression (IV), and as the integration is made on the surface of the
hemisphere, it depends on two variables θ e ϕ, we have a double integral
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint {\frac{\sigma r^{2}\sin \theta \;d\theta\;d\phi}{r^{3}}}\;\mathbf{r}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\sigma \sin \theta\;d\theta \;d\phi}{r}}\;\mathbf{r} \tag{VIII}
\end{gather}
\]
substituting expressions (I) and (II) into expression (VIII)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint{\frac{\sigma \sin \theta \;d\theta \;d\phi}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}-z\;\mathbf{k}\right) \tag{IX}
\end{gather}
\]
substituting expression (II) into expression (IX)
\[
\begin{align}
& \mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint {\frac{\sigma \sin \theta \;d\theta \;d\phi}{\left[\left(a\sin \theta \cos \phi\right)^{2}+\left(a\sin \theta \sin \phi\right)^{2}+\left(a\cos \theta\right)^{2}\right]^{\frac{1}{2}}}}\;\times \\
& \qquad\qquad\qquad\qquad\qquad\qquad \times \;\left(-a\sin \theta \cos \phi\;\mathbf{i}-a\sin \theta\sin \phi \;\mathbf{j}-a\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\sigma \sin \theta\;d\theta \;d\phi}{\left[a^{2}\sin ^{2}\theta \cos^{2}\phi +a^{2}\sin ^{2}\theta \sin ^{2}\phi+a^{2}\cos ^{2}\theta \right]^{\frac{1}{2}}}}\;\times \\
& \qquad\qquad\qquad\qquad\qquad\qquad \times \;\left(-a\sin \theta \cos \phi\;\mathbf{i}-a\sin \theta\sin \phi \;\mathbf{j}-a\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{-a\sigma \sin \theta\;d\theta \;d\phi}{a\left[\sin ^{2}\theta \cos ^{2}\phi+\sin ^{2}\theta \sin ^{2}\phi +\cos^{2}\theta \right]^{\frac{1}{2}}}}\;\times \\
& \qquad\qquad\qquad\qquad\qquad\qquad \times \;\left(\sin \theta \cos\phi \;\mathbf{i}+\sin \theta\sin \phi \;\mathbf{j}+\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{-\sigma \sin \theta\;d\theta \;d\phi}{\left[\sin ^{2}\theta \cos ^{2}\phi+\sin ^{2}\theta \sin ^{2}\phi +\cos^{2}\theta \right]^{\frac{1}{2}}}}\;\times \\
& \qquad\qquad\qquad\qquad\qquad\qquad \times \;\left(\sin \theta \cos\phi \;\mathbf{i}+\sin \theta\sin \phi \;\mathbf{j}+\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{-\sigma \sin \theta\;d\theta \;d\phi}{\left[\sin ^{2}\theta\underbrace{\left(\cos ^{2}\phi +\sin ^{2}\phi\right)}_{1}+\cos ^{2}\theta\right]^{\frac{1}{2}}}}\;\times \\
& \qquad\qquad\qquad\qquad\qquad\qquad \times \;\left(\sin \theta \cos \phi\;\mathbf{i}+\sin \theta\sin \phi \;\mathbf{j}+\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{-\sigma \sin \theta\;d\theta \;d\phi}{\left[\underbrace{\sin ^{2}\theta+\cos ^{2}\theta}_{1}\right]^{\frac{1}{2}}}}\left(\sin \theta \cos \phi\;\mathbf{i}+\sin \theta\sin \phi \;\mathbf{j}+\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{-\sigma \sin \theta\;d\theta \;d\phi}{1^{\frac{1}{2}}}}\left(\sin \theta\cos \phi \;\mathbf{i}+\sin \theta\sin \phi \;\mathbf{j}+\cos \theta\;\mathbf{k}\right)\\[10pt]
& \mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {-\sigma \sin \theta \;d\theta\;d\phi}\left(\sin \theta \cos \phi\;\mathbf{i}+\sin \theta\sin \phi;\mathbf{j}+\cos \theta\;\mathbf{k}\right)
\end{align}
\]
As the charge density σ is constant it is moved outside of the integral, and the integral of the sum
is equal to the sum of the integrals,
\[
\begin{gather}
\mathbf{E}=-\frac{\sigma}{4\pi\epsilon_{0}}\left(\iint {\sin ^{2}\theta \cos \phi\;d\theta \;d\phi\;\mathbf{i}}+\iint{\sin ^{2}\theta \sin \phi \;d\theta \;d\phi\;\mathbf{j}}+\iint {\sin \theta \;\cos \theta \;d\theta \;d\phi\;\mathbf{k}}\right)
\end{gather}
\]
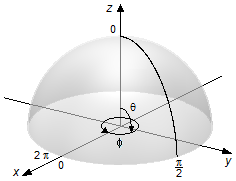
The limits of integration will be 0 and 2π in dϕ, a full turn on the base of the hemisphere,
and 0 to
\( \frac{\pi}{2} \)
in dθ (Figure 2), the integral can be separated.
\[
\begin{gather}
\mathbf{E}=-\frac{\sigma}{4\pi\epsilon_{0}}\left(\int_{0}^{{\frac{\pi}{2}}}{\sin ^{2}\theta\;d\theta }\underbrace{\int_{0}^{{2\pi}}{\cos \phi \;d\phi}}_{0}\;\mathbf{i}+\int_{0}^{{\frac{\pi}{2}}}{\sin ^{2}\theta \;d\theta \underbrace{\int_{0}^{{2\pi}}{\sin \phi \;d\phi}}_{0}\;\mathbf{j}}\right.\text{+}\\
\qquad \qquad \text{+}\left.\int_{0}^{{\frac{\pi}{2}}}{\sin \theta \cos \theta \;d\theta}\int_{0}^{{2\pi}}{d\phi\;\mathbf{k}}\right)
\end{gather}
\]
Integration of \( \displaystyle \int_{0}^{{2\pi}}\cos \phi \;d\phi \)
1st method
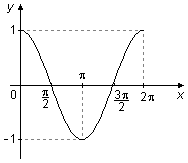Figure 3
1st method
\[
\begin{align}
\int_{0}^{{2\pi}}\cos \phi \;d\phi &=\left.\sin \phi\;\right|_{\;0}^{\;2\pi}=\sin 2\pi-\sin 0=\\
&=0-0=0
\end{align}
\]
2nd method
The graph of cosine between 0 and 2π, has a "positive" area above the x-axis between 0 and \( \frac{\pi}{2} \) and between \( \frac{3\pi}{2} \) and 2π, and a "negative" area below the x-axis between \( \frac{\pi}{2} \) and \( \frac{3\pi}{2} \), these two areas cancel in the integration and the integral is equal to zero (Figure 3).
The graph of cosine between 0 and 2π, has a "positive" area above the x-axis between 0 and \( \frac{\pi}{2} \) and between \( \frac{3\pi}{2} \) and 2π, and a "negative" area below the x-axis between \( \frac{\pi}{2} \) and \( \frac{3\pi}{2} \), these two areas cancel in the integration and the integral is equal to zero (Figure 3).
Integration of \( \displaystyle \int_{0}^{{2\pi}}\sin \phi \;d\phi \)
1st method
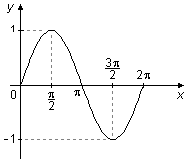Figure 4
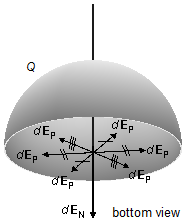Figure 5
1st method
\[
\begin{align}
\int_{0}^{{2\pi}}\sin \phi \;d\phi &=\left.-\cos \phi\;\right|_{\;0}^{\;2\pi}=-(\cos 2\pi-\cos 0)=\\
&=-(1-1)=0
\end{align}
\]
2nd method
The graph of sine between 0 and 2π, has a "positive" area above the x-axis between 0 and π and a "negative" area below the x-axis between π and 2π, these two areas cancel in the integration and the integral is equal to zero (Figure 4).
The graph of sine between 0 and 2π, has a "positive" area above the x-axis between 0 and π and a "negative" area below the x-axis between π and 2π, these two areas cancel in the integration and the integral is equal to zero (Figure 4).
Note: The two integrals, in directions i and j which are zero, represent
the mathematical calculation for the assertion that is usually done that the components of the
electric field parallel to the xy plane, dEP, cancel. Only
normal components to the plane dEN contribute to the total electric
field (Figure 5).
Integration of \( \displaystyle \int_{0}^{{\frac{\pi}{2}}}\sin \theta \cos \theta\;d\theta \)
Changing the variable
for θ = 0
we have \( u=\sin 0\Rightarrow u=0 \)
for \( \theta =\dfrac{\pi}{2} \)
we have \( u=\sin \dfrac{\pi}{2}\Rightarrow u=1 \)
Changing the variable
\[
\begin{array}{l}
u=\sin \theta \\[5pt]
\dfrac{du}{d\theta }=\cos \theta \Rightarrow d\theta=\dfrac{du}{\cos \theta}
\end{array}
\]
changing the limits of integration
for θ = 0
we have \( u=\sin 0\Rightarrow u=0 \)
for \( \theta =\dfrac{\pi}{2} \)
we have \( u=\sin \dfrac{\pi}{2}\Rightarrow u=1 \)
\[
\begin{align}
\int_{0}^{1}u\cos \theta \frac{du}{\cos \theta} &=\int_{0}^{1}u\;du=\left.\frac{u^{2}}{2}\;\right|_{0}^{1}=\\[5pt]
&=\left(\frac{1^{2}}{2}-\frac{0^{2}}{2}\right)=\frac{1}{2}
\end{align}
\]
Integration of \( \displaystyle \int_{0}^{{2\pi}}\;d\phi \)
\[
\begin{gather}
\int_{0}^{{2\pi}}\;d\phi=\left.\phi \;\right|_{\;0}^{\;2\pi}=2\pi-0=2\pi
\end{gather}
\]
\[
\begin{gather}
\mathbf{E}=-\frac{\sigma}{4\pi\epsilon_{0}}\left[0\;\mathbf{i}-0\;\mathbf{j}+\frac{1}{2}.2\pi\;\mathbf{k}\right]\\[5pt]
\mathbf{E}=-\frac{\sigma}{4\epsilon_{0}}\;\mathbf{k} \tag{X}
\end{gather}
\]
The superficial density of charge is given by
\[
\begin{gather}
\sigma=\frac{Q}{A} \tag{XI}
\end{gather}
\]
where Q is the charge of the hemisphere and A its area. The area of a hemisphere is half the
area of a sphere,
\( A_{S}=4\pi r^{2} \)
with r = a
\[
\begin{gather}
A=\frac{A_{S}}{2}\\[5pt]
A=\frac{4\pi a^{2}}{2}\\[5pt]
A=2\pi a^{2} \tag{XII}
\end{gather}
\]
substituting the expression (XII) into expression (XI) and this into expression (X) (Figure 6)
\[
\begin{gather}
\mathbf{E}=-{\frac{1}{4\epsilon_{0}}}\frac{Q}{2\pi a^{2}}\;\mathbf{k}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=-{\frac{Q}{8\epsilon_{0}\pi a^{2}}}\;\mathbf{k}}
\end{gather}
\]
advertisement
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .