Solved Problem on Coulomb's Law and Electric Field
advertisement
A ring of radius a carries a uniformly distributed electric charge q1 in one of
the halves and q2 in another half. Calculate the electric field vector at a point
P on the symmetry axis perpendicular to the plane of the ring at a distance z from its
center.
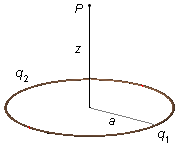
Problem data:
- Radius of the ring: a;
- Charge in one half of the ring: q1;
- Charge in the other half of the ring: q2;
- Distance to the point where we want the electric field: z.
- For the half of the ring with charge q1 between 0 and π
\[
\begin{gather}
{\mathbf{r}}_{1}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\end{gather}
\]

From the geometry of the problem, we choose cylindrical coordinates (Figure 1-B), the rq vector, which is on the xy plane, is written as \( {\mathbf{r}}_{q}=x\;\mathbf{i}+y\;\mathbf{j} \) and the rp vector only has a component in the k direction, \( {\mathbf{r}}_{p}=z\;\mathbf{k} \), the position vector will be
\[
\begin{gather}
{\mathbf{r}}_{1}=z\;\mathbf{k}-\left(x\;\mathbf{i}+y\;\mathbf{j}\right)\\[5pt]
{\mathbf{r}}_{1}=-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k} \tag{I}
\end{gather}
\]
From expression (I), the magnitude of the position vector r1 will be
\[
\begin{gather}
r_{1}^{2}=(-x)^{2}+(-y)^{2}+z^{2}\\[5pt]
r_{1}=\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
where x, y, and z, in cylindrical coordinates, are given by
\[
\begin{gather}
\left\{
\begin{array}{l}
x=a\cos \theta \\
y=a\sin \theta \\
z=z
\end{array}
\right. \tag{III}
\end{gather}
\]
The electric field vector of this half of the ring is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\end{gather}
\]
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq_{1}}{r^{2}}\frac{{\mathbf{r}}}{r}}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq_{1}}{r^{3}}{\mathbf{r}}} \tag{IV}
\end{gather}
\]
Using the expression of the linear density of charge λ1, we have the charge element
dq1
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\end{gather}
\]
\[
\begin{gather}
\lambda_{1}=\frac{dq_{1}}{ds_{1}}\\[5pt]
dq_{1}=\lambda_{1}\;ds_{1} \tag{V}
\end{gather}
\]
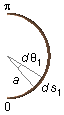
Figure 2
where ds1 is an arc element with angle dθ1 (Figure 2)
\[
\begin{gather}
ds_{1}=a\;d\theta_{1} \tag{VI}
\end{gather}
\]
substituting the expression (VI) into expression (V)
\[
\begin{gather}
dq_{1}=\lambda_{1}a\;d\theta_{1} \tag{VII}
\end{gather}
\]
Substituting expressions (I), (II), and (VII) into expression (IV)
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\int {\frac{\lambda_{1}a\;d\theta_{1}}{\left[\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right)\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda_{1}a\;d\theta_{1}}{\left(x^{2}+y^{2}+z^{2}\;\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right) \tag{VIII}
\end{gather}
\]
substituting expressions (III) into expression (VIII)
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\int {\frac{\lambda_{1}a\;d\theta_{1}}{\left[\left(a\cos \theta_{1}\right)^{2}+\left(a\sin \theta_{1}\right)^{2}+z^{2}\right]^{\frac{3}{2}}}\left(-a\cos \theta_{1}\;\mathbf{i}-a\sin \theta_{1}\;\mathbf{j}+z\mathbf{k}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda_{1}a\;d\theta_{1}}{\left[a^{2}\cos^{2}\theta_{1}+a^{2}\sin ^{2}\theta_{1}+z^{2}\right]^{\frac{3}{2}}}\left(-a\cos \theta_{1}\;\mathbf{i}-a\sin \theta_{1}\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda_{1}a\;d\theta_{1}}{\left[a^{2}\underbrace{\left(\cos ^{2}\theta_{1}+\sin ^{2}\theta_{1}\right)}_{1}+z^{2}\right]^{\frac{3}{2}}}\left(-a\cos \theta_{1}\;\mathbf{i}-a\sin \theta_{1}\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda_{1}a\;d\theta_{1}}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-a\cos \theta_{1}\;\mathbf{i}-a\sin \theta_{1}\;\mathbf{j}+z\;\mathbf{k}\right)}
\end{gather}
\]
As the charge density λ1 and the radius a are constants they are moved outside of
the integral, and the integral of the sum is equal to the sum of the integrals
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\frac{\lambda_{1}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-a\int \cos \theta_{1}\;d\theta_{1}\;\mathbf{i}-a\int\sin \theta_{1}\;d\theta_{1}\;\mathbf{j}+z\int \;d\theta_{1}\;\mathbf{k}\right)
\end{gather}
\]
The limits of integration, for this half of the ring, will be 0 and π (half-turn - Figure 2)
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\;\frac{\lambda_{1}a}{\left(a^{2}+z^{2}\;\right)^{\frac{3}{2}}}\left(-a\int_{0}^{\pi}\cos \theta _{1}\;d\theta_{1}\;\mathbf{i}-a\int_{0}^{\pi}\sin \theta_{1}\;d\theta_{1}\;\mathbf{j}+z\int_{0}^{\pi}\;d\theta_{1}\;\mathbf{k}\right)
\end{gather}
\]
Integration of \( \displaystyle \int_{0}^{\pi }\cos \theta_{1}\;d\theta_{1} \)
1st method
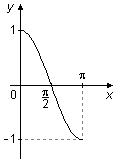
Figure 3
1st method
\[
\begin{align}
\int_{0}^{\pi}\cos \theta_{1}\;d\theta_{1} &=\left.\sin \theta_{1}\;\right|_{\;0}^{\;\pi}=\sin \pi -\sin 0=\\
&=0-0=0
\end{align}
\]
2nd method
The graph of cosine between 0 and π, has a "positive" area above the x-axis between 0 and \( \frac{\pi}{2} \), and a "negative" area below the x-axis, between \( \frac{\pi}{2} \) and π, these two areas cancel in the integration and the integral is equal to zero (Figure 3).
The graph of cosine between 0 and π, has a "positive" area above the x-axis between 0 and \( \frac{\pi}{2} \), and a "negative" area below the x-axis, between \( \frac{\pi}{2} \) and π, these two areas cancel in the integration and the integral is equal to zero (Figure 3).

Figure 3
Integration of \( \displaystyle \int_{0}^{\pi}\sin \theta_{1}\;d\theta_{1} \)
\[
\begin{align}
\int_{0}^{\pi}\sin \theta_{1}\;d\theta_{1} &=\left.-\cos\theta_{1}\;\right|_{\;0}^{\;\pi }=-(\cos \pi -\cos 0)\\
&=-(-1-1)=-(-2)=2
\end{align}
\]
Integration of \( \displaystyle \int_{0}^{\pi}\;d\theta_{1} \)
\[
\begin{gather}
\int_{0}^{\pi}\;d\theta_{1}=\left.\theta_{1}\;\right|_{\;0}^{\;\pi}=\pi -0=\pi
\end{gather}
\]
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\;\frac{\lambda_{1}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-a.0\;\mathbf{i}-2a\;\mathbf{j}+\pi z\;\mathbf{k}\right)\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\;\frac{\lambda_{1}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-2a\;\mathbf{j}+\pi z\;\mathbf{k}\right) \tag{IX}
\end{gather}
\]
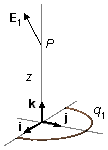
Figure 4
- For the half of the ring with charge q2 between π and 2π
\[
\begin{gather}
{\mathbf{E}}_{2}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq_{2}}{r^{3}}\;{\mathbf{r}}} \tag{X}
\end{gather}
\]
From the expression of linear density of charges (V), we have the element of charge dq2
\[
\begin{gather}
dq_{2}=\lambda_{2}\;ds_{2} \tag{XI}
\end{gather}
\]
substituting the expressions (I), (II), and (XI) into expression (X), we have a similar result to
the expression (VIII)
\[
\begin{gather}
{\mathbf{E}}_{2}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{\lambda_{2}a\;d\theta_{2}}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right) \tag{XII}
\end{gather}
\]
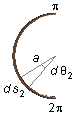
Figure 5
substituting expressions (III) into expression (XII) and following the same algebraic manipulation
\[
\begin{gather}
{\mathbf{E}}_{2}=\frac{1}{4\pi \epsilon_{0}}\;\frac{\lambda_{2}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-a\int \cos \theta_{2}\;d\theta_{\;2}\;\mathbf{i}-a\int\sin \theta_{2}\;d\theta_{2}\;\mathbf{j}+z\int \;d\theta_{2}\;\mathbf{k}\right)
\end{gather}
\]
The limits of integration, for this half of the ring, will be π and 2π (half-turn - Figure 5)
\[
\begin{gather}
{\mathbf{E}}_{2}=\frac{1}{4\pi \epsilon_{0}}\frac{\lambda_{2}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-a\int_{\pi}^{{2\pi}}\cos \theta_{2}\;d\theta_{2}\;\mathbf{i}-a\int_{\pi}^{{2\pi}}\sin \theta_{2}\;d\theta_{2}\;\mathbf{j}+z\int_{\pi}^{{2\pi}}\;d\theta_{2}\;\mathbf{k}\right)
\end{gather}
\]
Integration of \( \displaystyle \int_{\pi}^{{2\pi}}\cos \theta_{2}\;d\theta_{2} \)
1st method
 Figure 6
Figure 6
1st method
\[
\begin{align}
\int_{\pi}^{{2\pi}}\cos \theta_{2}\;d\theta_{2} &=\left.\sin \theta_{2}\;\right|_{\;\pi }^{\;2\pi}=\sin 2\pi -\sin \pi =\\
&=0-0=0
\end{align}
\]
2nd method
The graph of cosine between π and 2π has a "negative" area below the x-axis between π and \( \frac{3\pi}{2} \), and a "positive" area above the x-axis between \( \frac{3\pi}{2} \) and 2π, these two areas cancel in the integration and the integral is equal to zero (Figure 6).
The graph of cosine between π and 2π has a "negative" area below the x-axis between π and \( \frac{3\pi}{2} \), and a "positive" area above the x-axis between \( \frac{3\pi}{2} \) and 2π, these two areas cancel in the integration and the integral is equal to zero (Figure 6).

Integration of \( \displaystyle \int_{\pi}^{{2\pi}}\sin \theta_{2}\;d\theta_{2} \)
\[
\begin{align}
\int_{\pi}^{{2\pi}}\sin \theta_{2}\;d\theta_{2} &=\left.-\cos \theta_{2}\;\right|_{\;\pi}^{\;2\pi}=-(\cos 2\pi \cos \pi )=\\
&=-[1-(-1)]=-(2)=-2
\end{align}
\]
Integration of \( \displaystyle \int_{\pi}^{{2\pi}}\;d\theta_{2} \)
\[
\begin{gather}
\int_{\pi}^{{2\pi}}\;d\theta_{2}=\left.\theta_{2}\;\right|_{\;\pi}^{\;2\pi}=2\pi -\pi =\pi
\end{gather}
\]
\[
\begin{gather}
{\mathbf{E}}_{2}=\frac{1}{4\pi\epsilon_{0}}\;\frac{\lambda_{2}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[-a.0\;\mathbf{i}-(-2)a\;\mathbf{j}+\pi z\;\mathbf{k}\right]\\[5pt]
{\mathbf{E}}_{2}=\frac{1}{4\pi\epsilon_{0}}\;\frac{\lambda_{2}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(2a\;\mathbf{j}+\pi z\;\mathbf{k}\right) \tag{XIII}
\end{gather}
\]
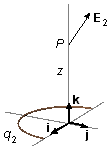
Figure 7
The total electric field vector is given by the sum of the expressions (IX) and (XIII)
\[
\begin{gather}
\mathbf{E}={\mathbf{E}}_{1}+{\mathbf{E}}_{2}
\end{gather}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{\lambda_{1}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-2a\;\mathbf{j}+\pi z\;\mathbf{k}\right)+\frac{1}{4\pi \epsilon_{0}}\frac{\lambda_{2}a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(2a\;\mathbf{j}+\pi z\;\mathbf{k}\right)\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-2a\lambda_{1}\;\mathbf{j}+\pi z\lambda_{1}\;\mathbf{k}+2a\lambda_{2}\;\mathbf{j}+\pi z\lambda_{2}\;\mathbf{k}\right)\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[2a\left(\lambda_{2}-\lambda_{1}\right)\;\mathbf{j}+\pi z\left(\;\lambda_{1}+\lambda_{2}\right)\;\mathbf{k}\right] \tag{XIV}
\end{gather}
\]
The charges of each half of the ring are q1 and q2, and their lengths
are πa, the linear density of charges of each half will be
\[
\begin{gather}
\lambda_{1}=\frac{q_{1}}{\pi a}\qquad \text{e}\qquad \lambda_{2}=\frac{q_{2}}{\pi a}
\end{gather}
\]
substituting these expressions into expression (XIV)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[2a\left(\frac{q_{2}}{\pi a}-\frac{q_{1}}{\pi a}\right)\;\mathbf{j}+\pi z\left(\frac{q_{1}}{\pi a}+\frac{q_{2}}{\pi a}\right)\;\mathbf{\text{k}}\right]\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[\frac{2\cancel{a}}{\pi \cancel{a}}\left(q_{2}-q_{1}\right)\;\mathbf{j}+\frac{\cancel{\pi} z}{\cancel{\pi} a}\left(q_{1}+q_{2}\right)\;\mathbf{k}\right]
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[\frac{2}{\pi}\left(q_{2}-q_{1}\right)\;\mathbf{j}+\frac{z}{a}\left(q_{1}+q_{2}\right)\;\mathbf{k}\right]}
\end{gather}
\]
Note: If the charge q1 is greater than the charge q2,
the term in the j direction will be negative
\( q_{2}-q_{1}<0 \),
and the electric field vector is in the directions &minu;j and k (Figure 8-A); if the
charge q1 is least than the charge q2, the term in the j
direction will be positive,
\( q_{2}-q_{1}>0 \),
and the electric field vector is in the direction +j and k (Figure 8-B), if
q1 and q2 charges are equal
\( \left(q_{1}=q_{2}=\frac{Q}{2}\right) \),
each half of the ring has half of the charge
\( \frac{Q}{2} \),
then the electric field vector expression
 Figure 8
Figure 8

\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[\frac{2}{\pi}\underbrace{\left(\frac{Q}{2}-\frac{Q}{2}\right)}_{0}\;\mathbf{j}+\frac{z}{a}\underbrace{\left(\frac{Q}{2}+\frac{Q}{2}\right)}_{Q}\;\mathbf{k}\right]\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{a}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\left[\frac{2}{\pi}.0\;\mathbf{j}+\frac{z}{a}Q\;\mathbf{k}\right]\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{\cancel{a}}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\frac{z}{\cancel{a}}Q\;\mathbf{k}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{\left(a^{2}+z^{2}\right)^{\frac{3}{2}}}\;\mathbf{k}
\end{gather}
\]
and so the result is obtained for the electric field vector of a ring uniform charge. (Figure 8-C).
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .