Solved Problem on Coulomb's Law and Electric Field
advertisement
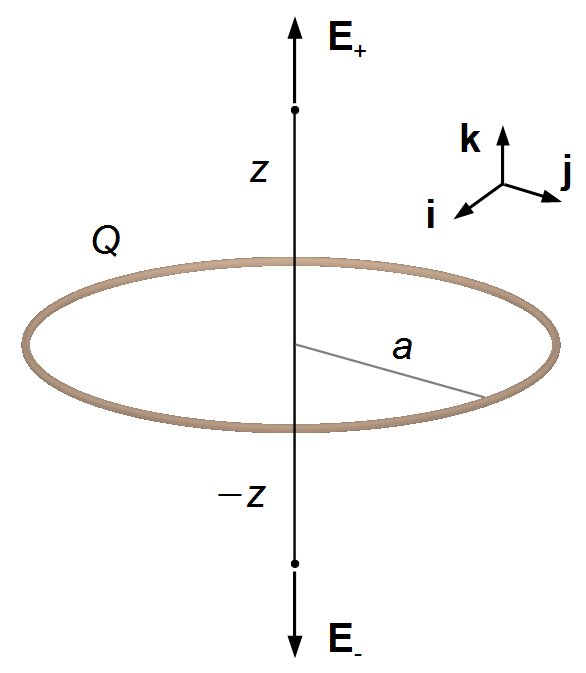
A ring of radius a is uniformly charged with a charge Q. The electric field produced by this ring at points on the axis of symmetry perpendicular to the plane of the ring at a distance z is given, in magnitude, by
\[
\begin{gather}
E=\frac{1}{4\pi \epsilon_{0}}\frac{Qz}{\left(a^{2}+z^{2}\right)^{3/2}}
\end{gather}
\]
Determine:
a) For what values of z is the electric field maximum?
b) What is this maximum value.
Solution
a) To find the maximum value of the electric field, we derive the function of the electric field with respect to z, E(z), and set it equal to zero
\[
\begin{gather}
\frac{dE}{dz}=0
\end{gather}
\]
Differentiation of \( \displaystyle E(z)=\frac{1}{4\pi \epsilon_{0}}\frac{Qz}{\left(a^{2}+z^{2}\right)^{3/2}} \)
The function E(z) is the quotient of two functions, using the quotient rule
The function E(z) is the quotient of two functions, using the quotient rule
\[
\begin{gather}
\left(\frac{u}{v}\right)^{'}=\frac{u'v-uv'}{v^{2}}
\end{gather}
\]
where
\( u(z)=z \)
and
\( v(z)=\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}} \)
\[
\begin{gather}
\frac{dE}{dz}=\frac{Q}{4\pi \epsilon_{0}}\frac{\dfrac{d(z)}{dz}\left(a^{2}+z^{2}\right)^{3/2}-(z)\dfrac{d\left[\left(a^{2}+z^{2}\right)^{3/2}\right]}{dz}}{\left[\left(a^{2}+z^{2}\right)^{3/2}\right]^{2}}
\end{gather}
\]
the function v(z) is a composite function, using the Chain Rule
\[
\begin{gather}
\frac{dv[w(z)]}{dz}=\frac{dv}{dw}\frac{dw}{dz}
\end{gather}
\]
where
\( v(w)=w^{3/2} \)
and
\( w(z)=a^{2}+z^{2} \)
\[
\begin{gather}
\frac{dE}{dz}=\frac{Q}{4\pi \epsilon_{0}}\frac{1.\left(a^{2}+z^{2}\right)^{3/2}-z\left[\dfrac{d\left(w^{3/2}\right)}{dg}\dfrac{d\left(a^{2}+z^{2}\right)}{dz}\right]}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\frac{\left(a^{2}+z^{2}\right)^{3/2}-z\left[\left(\dfrac{3}{2}w^{\frac{3}{2}-1}\right)(2z)\right]}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\frac{\left(a^{2}+z^{2}\right)^{3/2}-z\dfrac{3}{\cancel{2}}\left(a^{2}+z^{2}\right)^{1/2}\cancel{2}z}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\frac{\left(a^{2}+z^{2}\right)^{3/2}-3\left(a^{2}+z^{2}\right)^{1/2}z^{2}}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\left[\frac{\left(a^{2}+z^{2}\right)^{3/2}}{\left(a^{2}+z^{2}\right)^{3}}-\frac{3\left(a^{2}+z^{2}\right)^{1/2}z^{2}}{\left(a^{2}+z^{2}\right)^{3}}\right]\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\left[\frac{1}{\left(a^{2}+z^{2}\right)^{3}\left(a^{2}+z^{2}\right)^{-3/2}}-\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{3}\left(a^{2}+z^{2}\right)^{-1/2}}\right]\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\left[\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}}-\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{5/2}}\right]
\end{gather}
\]
Setting the derivative to zero
\[
\begin{gather}
\frac{Q}{4\pi \epsilon_{0}}\left[\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}}-\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{5/2}}\right]=0\\[5pt]
\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}}=\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{5/2}}\\[5pt]
\frac{\left(a^{2}+z^{2}\right)^{5/2}}{\left(a^{2}+z^{2}\right)^{3/2}}=3z^{2}\\[5pt]
\left(a^{2}+z^{2}\right)^{5/2}\left(a^{2}+z^{2}\right)^{-3/2}=3z^{2}\\[5pt]
\left(a^{2}+z^{2}\right)^{\frac{5}{2}-\frac{3}{2}}=3z^{2}\\[5pt]\left(a^{2}+z^{2}\right)^{\frac{2}{2}}=3z^{2}\\[5pt]
a^{2}+z^{2}=3z^{2}\\[5pt]
3z^{2}-z^{2}=a^{2}\\[5pt]
z^{2}=\frac{a^{2}}{2}\\[5pt]
z=\sqrt{\frac{a^{2}}{2}}\\[5pt]
z=\pm{\frac{a}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{z=\frac{a\sqrt{2}}{2}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{z=-{\frac{a\sqrt{2}}{2}}}
\end{gather}
\]
b) Substituting the values of z found in item (a) in the expression given in the problem
\[
\begin{gather}
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi \epsilon_{0}}\frac{Q\dfrac{a\sqrt{2}}{2}}{\left[a^{2}+\left(\dfrac{a\sqrt{2}}{2}\right)^{2}\right]^{3/2}}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\left[a^{2}+\dfrac{a^{2}}{2}\right]^{3/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\left[\dfrac{2a^{2}+a^{2}}{2}\right]^{3/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\left[\dfrac{3a^{2}}{2}\right]^{3/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\dfrac{3a^{2}}{2}\left[\dfrac{3a^{2}}{2}\right]^{1/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\dfrac{3a^{2}}{\cancel{2}}\dfrac{\cancel{a}\sqrt{3}}{\sqrt{2}}}\frac{\cancel{a}\sqrt{2}}{\cancel{2}}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{3a^{2}\sqrt{3}}\sqrt{2}\times\sqrt{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{1}{4\pi \epsilon _{0}}\frac{2Q}{3\sqrt{3}a^{2}}}
\end{gather}
\]
Note: The calculation made with the value
\( z=-{\frac{a\sqrt{2}}{2}} \)
gives the result
\[
\begin{gather}
E=-{\frac{1}{4\pi \epsilon_{0}}}\frac{2Q}{3\sqrt{3}a^{2}}
\end{gather}
\]
the minus sign indicates that the electric field vector is pointing in the opposite direction to the
unit vector k (Figure 1).
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .