Solved Problem on Heat

In what ratio must a certain mass M of water be divided initially at 20°C, under normal atmospheric pressure, assuming that all the energy taken from the part that freezes is used to evaporate the other part? Data:
Specific heat of water: 1 cal/g °C;
Latent heat of vaporization of water: 540 cal/g;
Latent heat of solidification of water: −80 cal/g.

Problem data:

Initial water temperature: t_i = 20 °C;
Mass of water: M;
Specific heat of water: c = 1 cal/g °C;
Latent heat of vaporization of water: L_V = 540 cal/g;
Latent heat of solidification of water: L_S = −80 cal/g.

Solution

The total mass of water will be the sum of the part that freezes, m_f, and the part that evaporates, m_v

\[ \begin{gather} M=m_{f}+m_{v} \tag{I} \end{gather} \]

The part of the water that freezes must first be cooled from the initial temperature of 20 °C to 0 °C, an amount of energy Q₁ must be removed by heat (Figure 1), then, keeping the temperature constant, the water is frozen by removing up an amount of energy by heat Q₂.

Figura 1

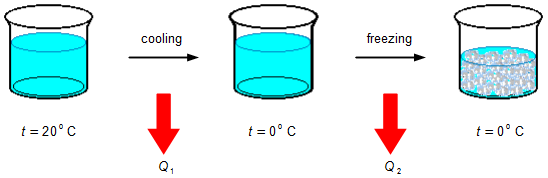
The amount of energy removed by heat in cooling is calculated by the heat transfer equation

\[ \begin{gather} \bbox[#99CCFF,10px] {Q=mc\left(t_{f}-t_{i}\right)} \tag{II} \end{gather} \]

where the final temperature will be t_f = 0 °C

\[ \begin{gather} Q_{1}=m_{f}c\left(t_{f}-t_{i}\right)\\ Q_{1}=m_{f}\times 1\times \left(0-20\right)\\ Q_{1}=-20m_{f} \tag{III} \end{gather} \]

the negative sign indicates that the water is losing energy.
The amount of energy removed by heat in freezing is calculated by the equation of the latent heat

\[ \begin{gather} \bbox[#99CCFF,10px] {Q=mL} \tag{IV} \end{gather} \]

\[ \begin{gather} Q_{2}=m_{f}L_{S}\\ Q_{2}=m_{f}\times (-80)\\ Q_{2}=-80m_{f} \tag{V} \end{gather} \]

The part of the water that evaporates must first be heated from the initial temperature of 20 °C to 100 °C, an amount of energy Q₃ must be supplied by heat (Figure 2), then, keeping the temperature constant, the water is evaporated giving up an amount of energy by heat Q₄.

Figure 2

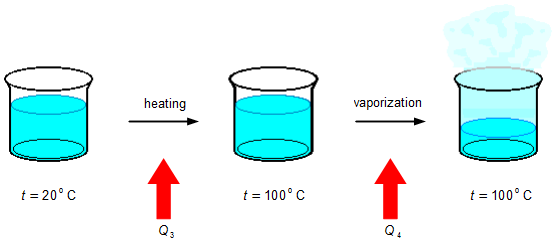
Using expression (II), with the final temperature t_f = 100 °C the energy supplied for heating will be

\[ \begin{gather} Q_{3}=m_{v}c\left(t_{f}-t_{i}\right)\\ Q_{3}=m_{v}\times 1\times \left(100-20\right)\\ Q_{3}=-80m_{v} \tag{VI} \end{gather} \]

The amount of energy supplied by heat for evaporation is given by expression (IV)

\[ \begin{gather} Q_{4}=m_{v}L_{v}\\ Q_{4}=m_{v}\times 540\\ Q_{4}=540m_{v} \tag{VII} \end{gather} \]

The problem tells us that all energy taken from the cooling part is used to evaporate the other part, the system is insulated and there is only heat exchange between the two parts of water, as heat is energy transferred, we can use the conservation of energy, "the sum of the heat transferred is equal to zero in a thermally insulated system"

\[ \bbox[#99CCFF,10px] {\sum Q=0} \]

\[ \begin{gather} Q_{1}+Q_{2}+Q_{3}+Q_{4}=0\\ -20m_{f}-80m_{f}+80m_{v}+540m_{v}=0\\ -100m_{f}+620m_{v}=0 \tag{VIII} \end{gather} \]

Using expression (I)

\[ \begin{gather} m_{f}=M-m_{v} \tag{IX} \end{gather} \]

substituting expression (IX) into expression (VIII)

\[ \begin{gather} -100\left(M-m_{v}\right)+620m_{v}=0\\ -100M+100m_{v}+620m_{v}=0\\ -100M+720m_{v}=0\\ 720m_{v}=100M\\ m_{v}=\frac{100}{720}M \end{gather} \]

\[ \bbox[#FFCCCC,10px] {m_{v}=0,139M} \]

Substituting this value in the expression (IX)

\[ m_{f}=M-0,139M \]

\[ \bbox[#FFCCCC,10px] {m_{f}=0,861M} \]

Note: From expression (VIII), we could also write

\[ \begin{gather} 620m_{v}=100m_{f}\\ \frac{m_{v}}{m_{f}}=\frac{100}{620}\\ \frac{m_{v}}{m_{f}}=\frac{5}{31} \end{gather} \]

This result means that for every 5 parts of water that evaporates, we have 31 parts of water that freeze.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .