Solved Problem on Gases
advertisement
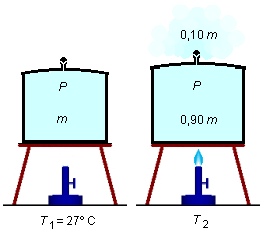
A metal container of a certain capacity is filled with air at 27 °C. The set is heated; the pressure remains constant due to the action of a valve that allows the escape of the air. To what temperature must the system be brought so that 10% of the mass of air initially placed in the container escapes? The coefficient of volume expansion of the metal is 0.0005 °C−1 and the air is assumed to be a ideal gas.
Problem data:
- coefficient of volume expansion of the metal : γ = 0.005 °C−1;
| Initial State | Final State |
|---|---|
| p1 = p | p2 = p |
| V1 | V2 |
| T1 = 27 °C = 300 K | T2 |
| n1 | n2 = 0.90 n1 |
Problem diagram:
As we want 10% of the air mass to escape, the other 90% of the mass should remain in the container. As
there is a direct relationship between the mass of a gas and its number of moles, therefore, if 10% of
the mass escapes from the container, then 10% of the number of moles of the gas escapes, and 90% remains
in the container (Figure 1).
Solution
As the gas is considered ideal, we can use the Equation of State for an Ideal Gas
\[
\begin{gather}
\bbox[#99CCFF,10px]
{pV=nRT}
\end{gather}
\]
applied to initial and final situations
\[
\begin{gather}
p_{1}V_{1}=n_{1}RT_{1} \tag{I}
\end{gather}
\]
\[
\begin{gather}
p_{2}V_{2}=n_{2}RT_{2} \tag{II}
\end{gather}
\]
where R is the universal gas constant, dividing expression (I) by expression (II)
\[
\begin{gather}
\frac{\cancel{p}V_{1}}{\cancel{p}V_{2}}=\frac{n_{1}\cancel{R}T_{1}}{n_{2}\cancel{R}T_{2}}\\[5pt]
\frac{V_{1}}{V_{2}}=\frac{n_{1}T_{1}}{n_{2}T_{2}} \tag{III}
\end{gather}
\]
To determine the relationship between the initial volumes, V1, and the final volumes,
V2, remember that the container undergoes expansion during the heating process, the
volumetric expansion of the container is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Delta V=V_{0}\gamma \Delta t}
\end{gather}
\]
applying to the problem, ΔV = V2 − V1,
V0 = V1 and
ΔT = T2 − T1
\[
\begin{gather}
V_{2}-V_{1}=V_{1}\gamma(T_{2}-T_{1})\\[5pt]
V_{2}=V_{1}+V_{1}\gamma(T_{2}-T_{1})\\[5pt]
V_{2}=V_{1}[1+\gamma(T_{2}-T_{1})]\\[5pt]
\frac{V_{2}}{V_{1}}=1+\gamma(T_{2}-T_{1}) \tag{IV}
\end{gather}
\]
inverting the fraction upside down of expression (III) and substituting in expression (IV)
\[
\begin{gather}
\frac{n_{2}T_{2}}{n_{1}T_{1}}=1+\gamma (T_{2}-T_{1})
\end{gather}
\]
solving the equation for T2
\[
\begin{gather}
\frac{n_{2}T_{2}}{n_{1}T_{1}}=1+\gamma T_{2}-\gamma T_{1}\\[5pt]
\frac{n_{2}T_{2}}{n_{1}T_{1}}-\gamma T_{2}=1-\gamma T_{1}\\[5pt]
T_{2}\left(\frac{n_{2}}{n_{1}T_{1}}-\gamma \right)=1-\gamma T_{1}\\[5pt]
T_{2}=\frac{1-\gamma T_{1}}{\dfrac{n_{2}}{n_{1}T_{1}}-\gamma}
\end{gather}
\]
using the data
\( \dfrac{n_{2}}{n_{1}}=0.90 \)
and substituting the values
\[
\begin{gather}
T_{2}=\frac{1-0.0005\times 300}{\dfrac{0.90}{300}-0.0005}\\[5pt]
T_{2}=\frac{1-0.15}{0.003-0.0005}\\[5pt]
T_{2}=\frac{0.85}{0.0025}\\[5pt]
T_{2}=340\;\text{K}
\end{gather}
\]
Converting from Kelvins (K) to degrees Celsius (°C)
\[
\begin{gather}
T=t_{C}+273\\[5pt]
t_{C}=T-273\\[5pt]
t_{C}=340-273\\[5pt]
t_{C}=67 \;°\text{C}
\end{gather}
\]
The final temperature will be
340 K
or
67 ºC.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .