Solved Problem on Pendulum

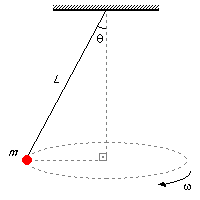
A body of mass m is attached to a rope, inextensible and lightweight, and rotates in a horizontal plane, this is a conical pendulum. The length of the rope is equal to L, and the angle that the rope makes with the vertical is equal to θ. Determine:
a) The tension force T on the rope;
b) The angular speed ω of rotation;
c) the period τ of the oscillations;
d) the tangential speed of the body.

Problem data:

Mass of the body: m;
Length of the rope: L;
Angle between the rope and the vertical: θ.

Problem diagram:

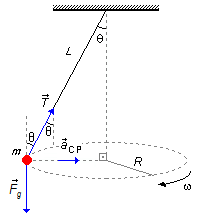
On the mass m acts the gravitational force \( \vec{F}_{g} \) and tension force \( \vec{T} \) on the rope. As the body is in a circular motion the centripetal acceleration \( {\vec{a}}_{cp} \), acts on it, pointing toward the center of the trajectory. The angle between the tension force on the rope and the vertical passing through the body is equal to θ, the same angle we have between the rope L and the vertical, are alternate angles (Figure 1).

Figure 1

Solution

a) Drawing the forces acting on the body in a coordinate system (Figure 2), we apply Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec{F}=m\vec{a}} \tag{I} \end{gather} \]

\( \vec{F}_{g} \): gravitational force on the body;
\( \vec{T} \): tension force on the rope.

In the vertical direction, the gravitational force and the component of the tension force in the y direction cancel

\[ \begin{gather} F_{g}=T_{y} \tag{II} \end{gather} \]

Figure 2

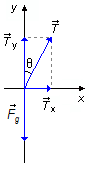
The angle θ measured between vector \( \vec{T} \) and y-axis, contrary to what is usually done where an angle is measured from the x-axis, we have that the component of tension in the y direction will be

\[ \begin{gather} T_{y}=T\cos \theta \tag{III} \end{gather} \]

the gravitational force is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_{g}=m g} \tag{IV} \end{gather} \]

substituting the expressions (III) and (IV) into expression (II)

\[ \begin{gather} T\cos \theta =m g \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {T=\frac{m g}{\cos \theta }} \end{gather} \]

b) From Figure 2 we write to a body in a circular motion, where the centripetal acceleration acts

\[ \begin{gather} \bbox[#99CCFF,10px] {{\vec{F}}_{cp}=m{\vec{a}}_{cp}} \end{gather} \]

the component of vector \( \vec{T} \) along the x-axis, \( T_{x} \), is the only force responsible for centripetal force \( {\vec{F}}_{cp} \)

\[ \begin{gather} F_{cp}=T_{x}=m a_{cp} \tag{V} \end{gather} \]

the component of the tension force in x direction is given by

\[ \begin{gather} T_{x}=T\sin \theta \tag{VI} \end{gather} \]

substituting T with the value found in the previous item

\[ \begin{gather} T_{x}=\frac{mg}{\cos \theta }\;\sin \theta \tag{VII} \end{gather} \]

The centripetal acceleration is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {a_{cp}=\frac{v^{2}}{R}} \tag{VIII} \end{gather} \]

substituting the expressions (VII) and (VIII) into expression (V)

\[ \begin{gather} \frac{\cancel{m} g}{\cos \theta }\;\sin \theta =\cancel{m}\frac{v^{2}}{R}\\[5pt] \frac{g}{\cos \theta }\;\sin \theta =\frac{v^{2}}{R} \tag{IX} \end{gather} \]

The tangential speed is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {v=\omega R} \tag{X} \end{gather} \]

substituting the expression (X) into expression (IX)

\[ \begin{gather} \frac{g}{\cos \theta }\,\sin \theta =\frac{(\omega R)^{2}}{R}\\[5pt] \frac{g}{\cos \theta }\,\sin \theta =\frac{\omega^{2}R^{\cancel{2}}}{\cancel{R}}\\[5pt] \frac{g}{\cos \theta }\,\sin \theta =\omega^{2}R \tag{XI} \end{gather} \]

The value of the radius R of the trajectory is not given in the problem, this value must be found as a function of the problem data (Figure 3)

\[ \begin{gather} \sin \theta =\frac{\text{opposite leg}}{\text{hypotenuse}}=\frac{R}{L}\\[5pt] R=L\sin \theta \tag{XII} \end{gather} \]

substituting the expression (XII) into expression (XI)

\[ \begin{gather} \frac{g}{\cos \theta }\,\cancel{\sin \theta} =\omega ^{2}L\cancel{\sin \theta}\\[5pt] \frac{g}{\cos \theta }=\omega ^{2}L\\[5pt] \omega^{2}=\frac{g}{L\cos \theta } \end{gather} \]

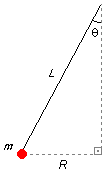
Figure 3

\[ \begin{gather} \bbox[#FFCCCC,10px] {\omega =\sqrt{\frac{g}{L\cos \theta }\;}} \end{gather} \]

c) The period τ is calculated using the expression for the angular velocity given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\omega =\frac{2\pi }{\tau}} \end{gather} \]

substituting the value of the angular velocity ω obtained in the previous item

\[ \begin{gather} \sqrt{\,\frac{g}{L\cos \theta }\,}=\frac{2\pi }{\tau}\\[5pt] \tau =\frac{2\pi }{\sqrt{\,\frac{g}{L\cos \theta}\,}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\tau =2\pi \sqrt{\,\frac{L\cos \theta }{g}\,}} \end{gather} \]

d) Substituting the solution of item (b) to the angular velocity ω and the expression (XII) into expression (X)

\[ \begin{gather} v=\sqrt{\frac{g}{L\cos \theta }\;}\;L\sin \theta \end{gather} \]

moving the term L sin θ within the root

\[ \begin{gather} v=\sqrt{\frac{g}{\cancel{L}\cos \theta }\;L^{\cancel{2}}\sin ^{2}\theta\;} \end{gather} \]

From the Trigonometry \( \tan \theta=\frac{\sin \theta}{\cos \theta} \)

\[ \begin{gather} v=\sqrt{\frac{g L\sin \theta\sin\theta}{\cos \theta }\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {v=\sqrt{g L\tan \theta \sin \theta}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .