Exercício Resolvido de Pêndulos

Um corpo de massa m está preso a uma corda, inextensível e de peso desprezível, e gira num plano horizontal constituindo um pêndulo cônico. O comprimento da corda é igual a L, O ângulo que a corda forma com a vertical é igual a θ. Determine:
a) A tensão T na corda;
b) A velocidade angular ω de rotação;
c) O período τ das oscilações;
d) A velocidade tangencial do corpo.

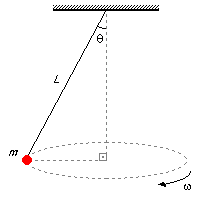
Dados do problema:

Massa do corpo: m;
Comprimento da corda: L;
Ângulo entre a corda e a vertical: θ.

Esquema do problema:

A massa m está sob a ação da força peso \( \vec{P} \) e da tensão \( \vec{T} \) na corda. Como o corpo realiza um movimento circular ele está sob a ação da aceleração centrípeta \( {\vec{a}}_{cp} \), apontada radialmente para o centro da trajetória. O ângulo entre a tensão na corda e a vertical passando pelo corpo é igual a θ, mesmo ângulo que temos entre a corda L e a vertical, são ângulos alternos internos (Figura 1).

Figura 1

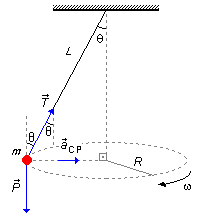
Solução

a) Desenhando as forças que atuam no corpo num sistema de eixos coordenados (Figura 2), aplicamos a 2.ª Lei de Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec{F}=m\vec{a}} \tag{I} \end{gather} \]

\( \vec{P} \): força peso do corpo;
\( \vec{T} \): força de tensão na corda.

Na direção vertical a força peso e a componente da força de tensão na direção y se anulam

\[ \begin{gather} P=T_{y} \tag{II} \end{gather} \]

Figura 2

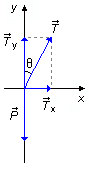
O ângulo θ medido entre o vetor \( \vec{T} \) e o eixo-y ao contrário do que se faz usualmente, em que se mede um ângulo a partir do eixo-x, temos que a componente da tração na direção de y será

\[ \begin{gather} T_{y}=T\cos \theta \tag{III} \end{gather} \]

a força peso é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {P=m g} \tag{IV} \end{gather} \]

substituindo as expressões (III) e (IV) na expressão (II)

\[ \begin{gather} T\cos \theta =m g \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {T=\frac{m g}{\cos \theta }} \end{gather} \]

b) Pela Figura 2 escrevemos para um corpo em movimento circular, onde atua a aceleração centrípeta

\[ \begin{gather} \bbox[#99CCFF,10px] {{\vec{F}}_{cp}=m{\vec{a}}_{cp}} \end{gather} \]

a componente do vetor \( \vec{T} \) ao longo do eixo-x, \( T_{x} \), é a única força responsável pela força centrípeta \( {\vec{F}}_{cp} \)

\[ \begin{gather} F_{cp}=T_{x}=m a_{cp} \tag{V} \end{gather} \]

a componente da força de tensão na direção x é dada por

\[ \begin{gather} T_{x}=T\operatorname{sen}\theta \tag{VI} \end{gather} \]

substituindo T pelo valor encontrado no item anterior

\[ \begin{gather} T_{x}=\frac{mg}{\cos \theta }\;\operatorname{sen}\theta \tag{VII} \end{gather} \]

A aceleração centrípeta é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {a_{cp}=\frac{v^{2}}{R}} \tag{VIII} \end{gather} \]

substituindo as expressões (VII) e (VIII) na expressão (V)

\[ \begin{gather} \frac{\cancel{m} g}{\cos \theta }\;\operatorname{sen}\theta =\cancel{m}\frac{v^{2}}{R}\\[5pt] \frac{g}{\cos \theta }\;\operatorname{sen}\theta =\frac{v^{2}}{R} \tag{IX} \end{gather} \]

A velocidade tangencial é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {v=\omega R} \tag{X} \end{gather} \]

substituindo a expressão (X) na expressão (IX)

\[ \begin{gather} \frac{g}{\cos \theta }\,\operatorname{sen}\theta =\frac{(\omega R)^{2}}{R}\\[5pt] \frac{g}{\cos \theta }\,\operatorname{sen}\theta =\frac{\omega^{2}R^{\cancel{2}}}{\cancel{R}}\\[5pt] \frac{g}{\cos \theta }\,\operatorname{sen}\theta =\omega^{2}R \tag{XI} \end{gather} \]

O valor do raio R da trajetória não é fornecido pelo problema, é preciso encontrar esse valor em função dos dados do problema (Figura 3)

\[ \begin{gather} \operatorname{sen}\theta =\frac{\text{cateto oposto}}{\text{hipotenusa}}=\frac{R}{L}\\[5pt] R=L\operatorname{sen}\theta \tag{XII} \end{gather} \]

substituindo a expressão (XII) na expressão (XI)

\[ \begin{gather} \frac{g}{\cos \theta }\,\cancel{\operatorname{sen}\theta} =\omega ^{2}L\cancel{\operatorname{sen}\theta}\\[5pt] \frac{g}{\cos \theta }=\omega ^{2}L\\[5pt] \omega^{2}=\frac{g}{L\cos \theta } \end{gather} \]

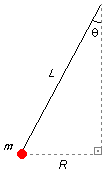
Figura 3

\[ \begin{gather} \bbox[#FFCCCC,10px] {\omega =\sqrt{\frac{g}{L\cos \theta }\;}} \end{gather} \]

c) O período τ é calculado usando a expressão para a velocidade angular dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {\omega =\frac{2\pi }{\tau}} \end{gather} \]

substituindo o valor da velocidade angular ω obtido no item anterior

\[ \begin{gather} \sqrt{\,\frac{g}{L\cos \theta }\,}=\frac{2\pi }{\tau}\\[5pt] \tau =\frac{2\pi }{\sqrt{\,\frac{g}{L\cos \theta}\,}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\tau =2\pi \sqrt{\,\frac{L\cos \theta }{g}\,}} \end{gather} \]

d) Substituindo a solução do item (b) para a velocidade angular ω e a expressão (XII) na expressão (X)

\[ \begin{gather} v=\sqrt{\frac{g}{L\cos \theta }\;}\;L\operatorname{sen}\theta \end{gather} \]

colocando o termo L sen θ dentro da raiz

\[ \begin{gather} v=\sqrt{\frac{g}{\cancel{L}\cos \theta }\;L^{\cancel{2}}\operatorname{sen}^{2}\theta\;} \end{gather} \]

Lembrando da Trigonometria \( \operatorname{tg} \theta=\frac{\operatorname{sen}\theta;}{\cos \theta} \)

\[ \begin{gather} v=\sqrt{\frac{g L\operatorname{sen}\theta\operatorname{sen}\theta}{\cos \theta }\;} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {v=\sqrt{g L\operatorname{tg}\theta \operatorname{sen}\theta}} \end{gather} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .