Solved Problem on Static Equilibrium
advertisement   



Two identical spheres, A and B, are placed in a box. The line connecting the centers of the two spheres makes an angle of 45° with the horizontal, and the reaction force exerted by the bottom of the box on sphere B is 25 N. Determine the reaction force that the box exerts on the spheres at the points of contact between the spheres and the box, and the force that sphere A exerts on sphere B.


Problem data:
  • Reaction force of the bottom of the box on sphere B:    FR = 25 N;
  • Angle between the line connecting the centers of the spheres and the horizontal:    θ = 45°;
  • Acceleration due to gravity:    g = 9.8 m/s2.
Problem diagram:

Figure 1

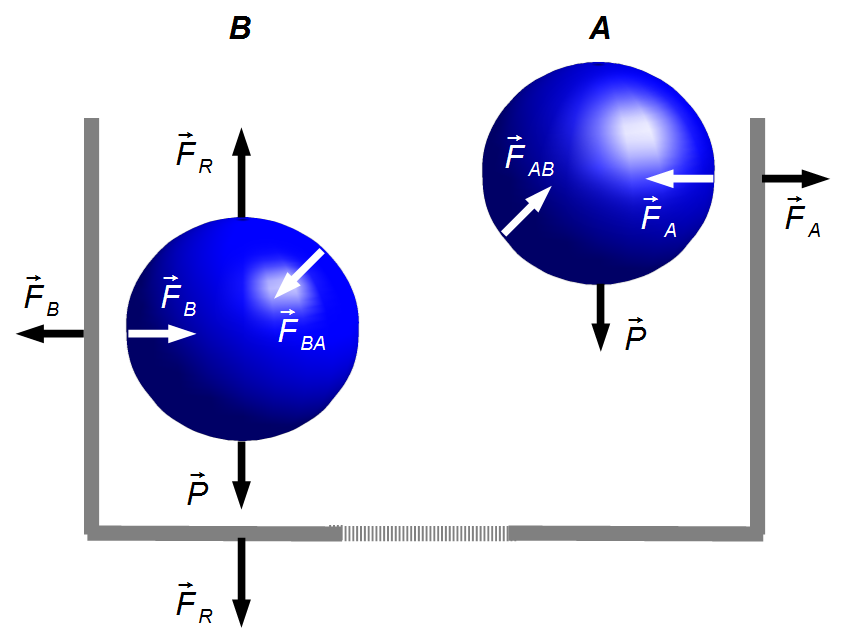
Drawing Free-Body Diagrams, we have the forces acting on the blocks (Figure 1).

  • Box:
    • \( -{\vec F}_R \): force that sphere B exerts on the bottom of the box;
    • \( {\vec F}_A \): force that sphere A exerts on the side wall of the box;
    • \( -{\vec F}_B \): force that sphere B exerts on the side wall of the box.
The weight of the box was neglected.
  • Sphere A:
    • \( {\vec F}_g \): gravitational force of sphere A;
    • \( {\vec F}_{AB} \): contact force on sphere A due to sphere B;
    • \( -{\vec F}_A \): reaction force of the box on sphere A.
  • Sphere B:
    • \( {\vec F}_g \): gravitational force of sphere B;
    • \( {\vec F}_{BA} \): contact force on sphere B due to sphere A, \( |\;{\vec{F}}_{BA}\;|=|\;{\vec{F}}_{AB}\;| \);
    • \( {\vec F}_R \): reaction force of the bottom of the box on sphere B;
    • \( {\vec F}_{B} \): reaction force of the box on sphere B.
Solution:

Since the system is in equilibrium, the resultant of the forces is equal to zero.
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum _i F_i=0} \tag{I} \end{gather} \]
We draw the forces in an xy coordinate system (Figures 2 and 3) and obtain their components along the x and y directions.
  • Sphere A:
    • x-direction:
      • \( F_{Ax}=-F_A \)
      • \( F_{ABx}=F_{AB}\cos\theta \)
Applying the equilibrium condition (I)
\[ \begin{gather} F_{ABx}-F_A=0 \\[5pt] F_{AB}\cos\theta-F_A=0 \tag{II} \end{gather} \]
Figure 2
  • Sphere A:
    • y-direction:
      • \( F_{gy}=-F_g \)
      • \( F_{ABy}=F_{AB}\sin\theta \)
Applying the equilibrium condition (I)
\[ \begin{gather} F_{ABy}-F_{gy}=0 \\[5pt] F_{AB}\sin \theta-F_g=0 \tag{III} \end{gather} \]
The gravitational force is given by
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{IV} \end{gather} \]
substituting equation (IV) into equation (III)
\[ \begin{gather} F_{AB}\sin\theta-mg=0 \tag{V} \end{gather} \]

  • Sphere B:
    • x-direction:
      • \( F_{Bx}=F_B \)
      • \( F_{BAx}=-F_{BA}\cos\theta=-F_{AB}\cos\theta \)
Applying the equilibrium condition (I)
\[ \begin{gather} F_B-F_{BAx}=0 \\[5pt] F_B-F_{AB}\cos\theta=0 \tag{VI} \end{gather} \]
Figure 3
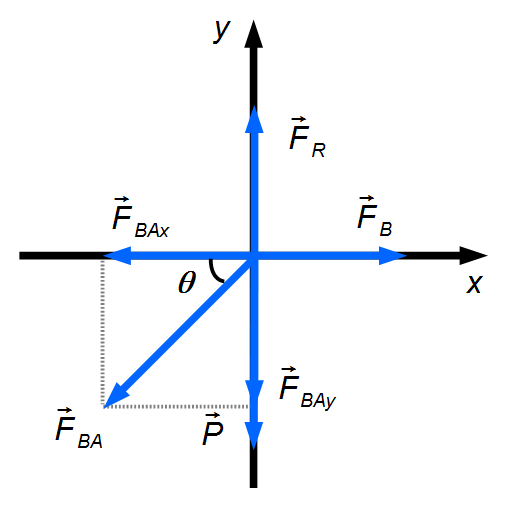
  • Sphere B:
    • y-direction:
      • \( F_{gy}=-F_g \)
      • \( F_{Ry}=F_R \)
      • \( F_{BAy}=-F_{BA}\sin\theta-F_{AB}\sin\theta \)
Applying the equilibrium condition (I)
\[ \begin{gather} F_R-F_{BAy}-P=0 \\[5pt] F_R-F_{AB}\sin\theta-P=0 \tag{VII} \end{gather} \]
substituting equation (IV) into equation (VII)
\[ \begin{gather} F_R-F_{AB}\sin\theta-mg=0 \tag{VIII} \end{gather} \]
Equations (II), (III), and (VIII) can be written as a system of three equations with four unknowns (FA, FAB, m and θ)
\[ \begin{gather} \left\{ \begin{array}{l} F_B-F_{AB}\cos\theta=0 \\ F_{AB}\cos\theta-F_A=0 \\ F_{AB}\sin\theta-mg=0 \\ F_R-F_{AB}\sin\theta-mg=0 \end{array} \right. \end{gather} \]
from the third equation of the system, we write
\[ \begin{gather} F_{AB}\sin\theta-mg=0 \\[5pt] F_{AB}\sin\theta=mg \end{gather} \]
substituting this value into the fourth equation of the system
\[ \begin{gather} F_R-mg-mg=0 \\[5pt] 2mg=F_R \\[5pt] m=\frac{F_R}{2g} \\[5pt] m=\frac{25\;\mathrm N}{2\times 9.8\;\mathrm{\frac{m}{s^2}}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {m=1.28\;\mathrm{kg}} \end{gather} \]
Substituting this value of mass into the third equation of the system
\[ \begin{gather} F_{AB}\operatorname{sen}\theta-mg=0 \\[5pt] F_{AB}=\frac{mg}{\operatorname{sen}\theta} \end{gather} \]

From Trigonometry, for θ = 45°,   \( \cos 45°=\operatorname{sen}45°=\frac{\sqrt{2\;}}{2} \)

\[ \begin{gather} F_{AB}=\frac{(1.28\;\mathrm{kg})\left(9.8\;\mathrm{\frac{m}{s^2}}\right)}{\dfrac{\sqrt{2\;}}{2}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{AB}=17.7\;\mathrm N} \end{gather} \]
Substituting this value of the force between spheres A and B into the first and second equations of the system
\[ \begin{gather} F_B-F_{AB}\cos\theta=0 \\[5pt] F_B=F_{AB}\cos\theta \\[5pt] F_B=(17.7\;\mathrm N)\times\frac{\sqrt{2\;}}{2} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_B=12.5\;\mathrm N} \end{gather} \]
\[ \begin{gather} F_{AB}\cos\theta-F_A=0 \\[5pt] F_A=F_{AB}\cos\theta \\[5pt] F_A=(17.7\;\mathrm N)\times\frac{\sqrt{2\;}}{2} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_A=12.5\;\mathrm N} \end{gather} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .