Solved Problem on Static Equilibrium

A body with a mass of 200 kg is kept in equilibrium on an inclined plane at an angle of 30° relative to the horizontal by a rope that passes over a fixed pulley and supports another body with a mass M at the other end. The rope makes a 45° angle with the inclined line of the plane. Determine:
a) The mass M;
b) The force exerted by the body against the plane.

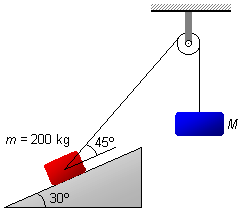
Problem data:

Mass of the body on the inclined plane: m=200 kg;
Angle of the inclined plane with the horizontal: 30°;
Angle of the rope with the inclined plane: 45°;
Acceleration due to gravity: g=9.8 m/s².

Problem diagram:

Drawing free-bodies diagrams, we have the forces acting on the blocks.

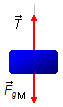
Body of mass M (Figure 1):
- \( \vec T \): tension force in the rope;
- \( {\vec F}_{gM} \): gravitational force of the suspended body.

Figure 1

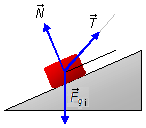
Body of mass 200 kg (Figure 2):
- \( \vec T \): tension force in the rope;
- \( {\vec F}_{gi} \): gravitational force of the body on the inclined plane;
- \( \vec N \): normal reaction force of the plane on the block.

Figure 2

Solution:

Since the system is in equilibrium, the resultant of the forces acting on it is zero.

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum \vec F=0} \tag{I} \end{gather} \]

Body of mass M (Figure 1):

There are no forces acting in the horizontal direction. In the vertical direction, the gravitational force \( {\vec F}_{gM} \) and the tension force \( \vec T \) cancel each other, applying condition (I)

\[ \begin{gather} T-P_M=0 \tag{II} \end{gather} \]

Body of mass 200 kg:

For the block on the inclined plane, we chose a frame of reference with the x-axis pointing upwards in the direction of the inclined plane and the y-axis perpendicular to it (Figure 3 on the left).
In the ΔAQM triangle, the leg \( \overline{QM} \) is represented by the gravitational force \( {\vec F}_g \). We need to find the angle that the gravitational force makes with the perpendicular y and parallel x directions to the inclined plane.
The angle \( Q\hat AM \) is given in the problem as 30°, and the segment \( \overline QM \) (the direction of the gravitational force) is perpendicular to the segment \( \overline AC \). Since the sum of the internal angles of a triangle equals 180°, then the angle \( A\hat QM \) must be

\[ \begin{gather} A\hat QM+30°+90°=180° \\[5pt] A\hat QM=180°-30°-90° \\[5pt] A\hat QM=60° \end{gather} \]

Figure 3

To determine the value of the angle α (Figure 3 on the right, enlarged)), the angle \( A\hat QM \) is equal to 60°, and the segment \( \overline{QN} \) is perpendicular to the segment \( \overline{AB} \), making an angle of 90°. Thus the sum of these angles with the angle α must be 180°

\[ \begin{gather} 60°+90°+\alpha=180° \\[5pt] \alpha=180°-60°-90° \\[5pt] \alpha=30° \end{gather} \]

By drawing the forces in a coordinate system xy (Figure 4), we obtain the components along the x and y directions.

Components along the x-axis

\( N_x=0 \)
\( T_x=T\cos 45° \)
\( F_{ix}=-F_i\cos 60° \)

Applying the equilibrium condition (I)

\[ \begin{gather} N_x+T\cos 45°-F_{gi}\cos 60°=0 \\[5pt] T\cos 45°-F_{gi}\cos 60°=0 \tag{III} \end{gather} \]

Figure 5

Components along the y-axis

\( N_y=N \)
\( T_y=T\sin 45° \)
\( F_{giy}=-F_{gi}\sin 60° \)

Applying the equilibrium condition (I)

\[ \begin{gather} N+T\sin 45°-F_{gi}\sin 60°=0 \tag{IV} \end{gather} \]

a) The gravitational force is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {F_g=mg} \end{gather} \]

From Trigonometry

\( \cos 45°=\sin 45°=\dfrac{\sqrt{2\;}}{2} \)
\( \cos 60°=\dfrac{1}{2} \), \( \sin 60°=\dfrac{\sqrt{3\;}}{2} \)

Equations (II), (III), and (IV) can be written as a system of three equations with three unknowns (N, T and M)

\[ \begin{gather} \left\{ \begin{array}{l} T-Mg=0 \\ \dfrac{\sqrt{2\;}}{2}T-\dfrac{1}{2}mg=0 \\ N+\dfrac{\sqrt{2\;}}{2}T-\dfrac{\sqrt{3\;}}{2}mg=0 \tag{V} \end{array} \right. \end{gather} \]

solving the first equation of the system (V) for the tension force

\[ \begin{gather} T=Mg \tag{VI} \end{gather} \]

substituting into the second equation system (V)

\[ \begin{gather} \frac{\sqrt{2\;}}{2}Mg-\frac{1}{2}mg=0\\[5pt] \frac{\sqrt{2\;}}{\cancel 2}M\cancel g=\frac{1}{\cancel 2}m\cancel g\\[5pt] \sqrt{2\;}M=m\\[5pt] M=\frac{m}{\sqrt{2\;}} \end{gather} \]

substituting the mass m given in the problem and \( \sqrt{2\;}\approx 1,4142 \)

\[ \begin{gather} M=\frac{200\;\mathrm{kg}}{1.4142} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {M=141.4\;\mathrm{kg}} \end{gather} \]

b) The force exerted on the plane \( F_p \) will be given by the y component of the gravitational force on the inclined plane

\[ \begin{gather} F_p=F_{giy}=-F_{gi}\sin 60° \\[5pt] F_p=-mg\sin 60° \\[5pt] F_p=-(200\;\mathrm{kg})\left(9.8\;\mathrm{\small{\frac{m}{s^2}}}\right) \frac{\sqrt{3\;}}{2} \end{gather} \]

where \( \sqrt{3\;}\approx 1.7321 \)

\[ \begin{gather} \bbox[#FFCCCC,10px] {F_p=-1697\;\mathrm N} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .