Two artificial satellites, S₁ and S₂ orbit the Earth in a circular motion at distances, respectively, equal to r₁ = R and r₂ = 3R from their center. At a certain instant, the line connecting the centers of the satellites is tangent to the orbit of S₁. Determine at this instant the distance d between S₁ and S₂.


Problem data:

• Distance from satellite S₁ to Earth:    r₁ = R;
• Distance from satellite S₂ to Earth:    r₂ = 3R.

Problem diagram:


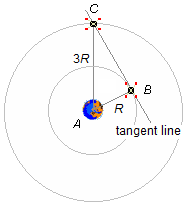
Solution

From Figure 1, we see that in the triangle ΔABC, segment \( \overline{AB} \) is the distance from satellite S₁ to Earth, segment \( \overline{AC} \) is the distance from satellite S₂ to Earth, segment \( \overline{BC} \) connects the centers of the two satellites and is tangent to the orbit of S₁ and perpendicular to \( \overline{AB} \), therefore the triangle ΔABC is a right triangle and the distance between the two satellites d, segment \( \overline{BC} \), will be given by the Pythagorean Theorem, we have the legs \( \overline{AB}=R \), \( \overline{BC}=d \) and the hypotenuse \( \overline{AC}=3R \)