Solved Problem on Kepler's Laws and Gravitation
advertisement
Determine the angular speed of a satellite around the Earth, assuming a circular orbit, as a function of the distance from the center of the Earth.
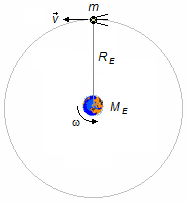
Problem diagram:
Let us assume that the following quantities are known, distance from Earth to satellite,
RE, the mass of Earth, ME, and
Newton's Universal Gravitational Constant, G.
Solution
The centripetal force for a satellite rotating around the Earth (Figure 1), is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{{\vec{F}}_{cp}=m{\vec{a}}_{cp}} \tag{I}
\end{gather}
\]
where m is the mass of the satellite, the centripetal acceleration is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_{cp}=\frac{v^{2}}{r}} \tag{II}
\end{gather}
\]
the tangential speed is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r} \tag{III}
\end{gather}
\]
substituting expression (III) into expression (II)
\[
\begin{gather}
a_{cp}=\frac{(\omega r)^{2}}{r}\\
a_{cp}=\frac{\omega^{2}r^{\cancel{2}}}{\cancel{r}}\\
a_{cp}=\omega^{2}r \tag{IV}
\end{gather}
\]
substituting expression (IV) into expression (I)
\[
\begin{gather}
F_{cp}=m\omega ^{2}r \tag{V}
\end{gather}
\]
The only force acting on the satellite is the gravitational force of attraction between the Earth and the
satellite given by Newton's Law of Universal Gravitation
A única força atuando no satélite é força de atração gravitacional da Terra dada pela
Lei da Gravitação Universal de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{G}=G\frac{Mm}{r^{2}}} \tag{VI}
\end{gather}
\]
this force is the centripetal resultant, substituting expression (V) into expression (VI), where
M = ME is the mass of the Earth, r = RE is the distance
from the satellite to the center of the Earth
\[
\begin{gather}
G\frac{M_{E}\cancel{m}}{R_{E}^{2}}=\cancel{m}\omega^{2}R_{E}
\end{gather}
\]
canceling the satellite mass m from both sides of the equation
\[
\begin{gather}
G\frac{M_{E}}{R_{E}^{2}}=\omega ^{2}R_{E}\\
\omega^{2}=G\frac{M_{E}}{R_{E}^{3}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\omega =\sqrt{G\frac{M_{E}}{R_{E}^{3}}\;}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .