Solved Problem on Resistors

Six resistors, each with resistance R, are arranged to form a tetrahedron, as shown. Determine the equivalent resistance between points A and B.

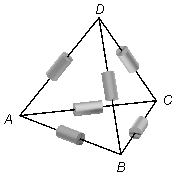
Solution

Point A is a node in the circuit, and the current at this point is divided equally between the resistors placed between points A and B, A and C, and A and D since all resistors have the same value R. The voltage between points A and D and A and C is the same, therefore points C and D are at the same potential, and no current flows through the resistor placed between these points. In this way, we can remove this resistor from the circuit (Figure 1). The voltage drop between A and B is different, it depends on the applied external voltage.

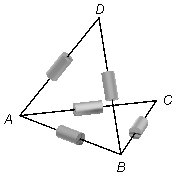Figure 1

This circuit can be represented as follows (Figure 2), the resistors between A and C and between C and B are in series, the resistors between A and D and between D and B are in series, and these sets are in parallel with the resistor between A and B.

Figure 2

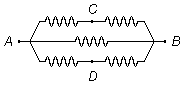
Let us call R₁ the equivalent resistor of the two resistors in series connected through C, and R₂ is the equivalent resistor of the two resistors in series connected through D, as these parts of the circuit are the same, we have that R₁ = R₂. The expression to determine the equivalent resistor of an association of n equal resistors connected in series is

\[ \begin{gather} \bbox[#99CCFF,10px] {R_{eq}=nR} \end{gather} \]

for n = 2

\[ \begin{gather} R_{1}=2 R \end{gather} \]

Note: We could also find the equivalent resistor by applying the general expression for associating resistors in series

\[ \begin{gather} R_{eq}=\sum_{i=1}^{n}R_{i}\\[5pt] R_{1}=R_{2}=R+R\\[5pt] R_{1}=R_{2}=2R \end{gather} \]

So the circuit reduces to what is shown in Figure 3, calculating the equivalent resistor of the parallel association

\[ \begin{gather} \bbox[#99CCFF,10px] {\frac{1}{R_{eq}}=\sum _{i=1}^{n}{\frac{1}{R_{i}}}} \end{gather} \]

\[ \begin{gather} \frac{1}{R_{eq}}=\frac{1}{R_{1}}+\frac{1}{R} \end{gather} \]

Figure 3

the common factor between R and 2R is 2R

\[ \begin{gather} \frac{1}{R_{eq}}=\frac{1+2+1}{2R}\\[5pt] \frac{1}{R_{eq}}=\frac{4}{2R}\\[5pt] R_{eq}=\frac{2R}{4} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {R_{eq}=\frac{R}{2}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .