Solved Problem on Electric Field
advertisement
Two equal charges of the same sign are separated by a distance 2d. Calculate the magnitude of the electric field at the points along the perpendicular bisector of the line joining the two charges. Check the solution for points far away from the center of the charges.
Construction of the resultant electric field vector:
On the bisector of the line that connect the charges, we choose any point P where we want to
calculate the electric field. In the direction of the straight line that connects one of the charges
+q to point P, we draw the vector
\( \vec E_1 \)
pointing outward from the charge, q>0 (Figure 1).

In the direction of the line segment that connects the other charge +q to point P, we
draw the vector
\( \vec E_2 \)
pointing outward from the charge, q>0 (Figure 2).

We draw a straight line through the end of vector
\( \vec E_1 \),
parallel to vector
\( \vec E_2 \)
(Figure 3).
We draw a straight line through the end of vector
\( \vec E_2 \),
parallel to vector
\( \vec E_1 \)
(Figure 4).
From point P to the intersection of the lines, we have the resultant vector
\( \vec E \),
and θ is the angle between the electric field vector
\( \vec E_2 \)
(or the vector
\( \vec E_1 \)
) and an auxliliary line parallel to a line that connects the two charges. The angle θ that
the electric field vectors,
\( \vec E_1 \)
and
\( \vec E_2 \),
make with the auxiliary line, is the same angle that the segment r makes with the vertical
segment d (Figure 5).

Note 1: this system does not represent an electric dipole, a dipole is formed
by charges of the same value and opposite signs, in this case we have charges of the same
sign.
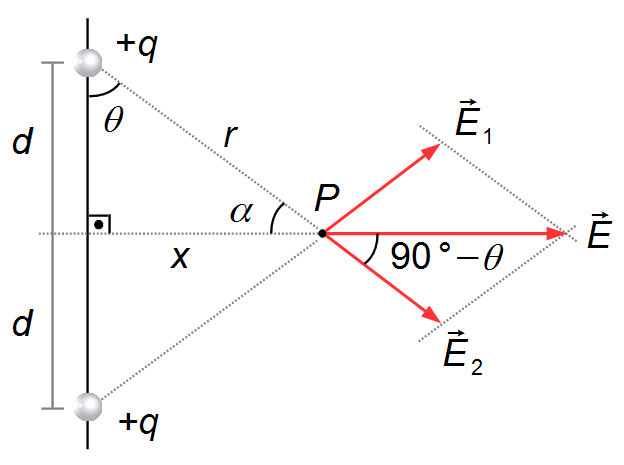 Figure 6
Figure 6
Note 2: instead of using the angle θ between the segment r and the
vertical segment d between the two charges, we could use the angle between the segment r
and the segment x (Figure 6). The sum of the interior angles of a triangle is equal to 180°
\[
\begin{gather}
180°=90°+\theta+\alpha\\[5pt]
\alpha=90°\theta
\end{gather}
\]

Solution:
The magnitude of the electric field of each charge is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E=k_e\frac{q}{r^2}} \tag{I}
\end{gather}
\]
The resultant electric field will be given by
\[
\begin{gather}
\vec E=\vec E_1+\vec E_2
\end{gather}
\]
as the charges have the same value in magnitude,
\( E_1=E_2 \)
\[
\begin{gather}
E=E_1\sin\theta+E_2\sin \theta\\[5pt]
E=2E_1\sin\theta \tag{II}
\end{gather}
\]
Note: using the cos 90°−θ obtained above, the electric field will be
\[
\begin{gather}
E=2E_1\;\cos(90°-\theta)
\end{gather}
\]
the difference formula for cosine is given by
\[
\begin{gather}
\cos (a-b)=\cos a\cos b+\sin a\sin b\\[10pt]
\cos (90°-\theta)=\underbrace{\cos90°}_0\cos\theta+\underbrace{\sin 90°}_1\sin\theta\\[5pt]
\cos(90°-\theta)=\sin \theta
\end{gather}
\]
The sine of θ is obtained from r and x
\[
\begin{gather}
\sin\theta=\frac{x}{r} \tag{III}
\end{gather}
\]
the segment r is obtained using the Pythagorean Theorem
\[
\begin{gather}
r^2=d^2+x^2\\[5pt]
r=\sqrt{d^2+x^2\;} \tag{IV}
\end{gather}
\]
substituting equation (IV) into equation (III)
\[
\begin{gather}
\sin \theta=\frac{x}{\sqrt{d^2+x^2\;}} \tag{V}
\end{gather}
\]
Substituting equations (I) and (V) into equation (II)
\[
\begin{gather}
E=2k_e\frac{q}{\left(\sqrt{d^2+x^2\;}\right)^2}\frac{x}{\sqrt{d^2+x^2\;}}\\[5pt]
E=2k_e\frac{q}{\left(d^2+x^2\right)}\frac{x}{\left(d^2+x^2\right)^{\frac{1}{2}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{2k_eqx}{\left(d^2+x^2\right)^{\frac{3}{2}}}}
\end{gather}
\]
For points far from the center of the dipole we have, x≫d, we can neglect the term in
d2 in the denominator and the solution will be
\[
\begin{gather}
E=\frac{2k_eqx}{x^{{\cancel 2}\times{\frac{3}{\cancel 2}}}} \\[5pt]
E=\frac{2k_eq\cancel x}{x^{\cancelto{2}{3}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{2k_eq}{x^2}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .