Exercício Resolvido de Choques
publicidade
Duas bolas absolutamente elásticas, de massas m1 e m2 e velocidades v1 e v2 respectivamente, chocam-se frontalmente, suas velocidades estão na direção da linha que une os seus centros. Determinar as velocidades das bolas após o choque nos casos:
a) A velocidade da segunda bola antes do choque é igual a zero;
b) As massas das bolas são iguais.
Dados do problema:
- Massa da bola 1: m1;
- Massa da bola 2: m2;
- Velocidade inicial da bola 1: v1;
- Velocidade inicial da bola 2: v2.
Adotamos um sistema de referência orientado para a direita, com a velocidade da bola 1 no mesmo sentido do referencial (v1 > 0) e a velocidade da bola 2 no sentido contrário (v2 < 0), Figura 1.

Solução
Como o choque é elástico a quantidade de movimento e a energia cinética do sistema se conservam. Assim escrevemos as equações para as bolas 1 e 2 nas situações inicial e final.
A quantidade de movimento é dada por
\[ \bbox[#99CCFF,10px]
{Q=mv}
\]
A energia cinética é dada por
\[ \bbox[#99CCFF,10px]
{E_{c}=\frac{mv^{2}}{2}}
\]
Antes do choque
\[
\begin{gather}
Q_{1i}=m_{1}v_{1} \tag{I}
\end{gather}
\]
\[
\begin{gather}
Q_{2i}=m_{2}v_{2} \tag{II}
\end{gather}
\]
\[
\begin{gather}
E_{1i}^{c}=\frac{m_{1}v_{1}^{2}}{2} \tag{III}
\end{gather}
\]
\[
\begin{gather}
E_{2i}^{c}=\frac{m_{2}v_{2}^{2}}{2} \tag{IV}
\end{gather}
\]
Depois do choque
\[
\begin{gather}
Q_{1f}=m_{1}v_{1f} \tag{V}
\end{gather}
\]
\[
\begin{gather}
Q_{2f}=m_{2}v_{2f} \tag{VI}
\end{gather}
\]
\[
\begin{gather}
E_{1f}^{c}=\frac{m_{1}v_{1f}^{2}}{2} \tag{VII}
\end{gather}
\]
\[
\begin{gather}
E_{2f}^{c}=\frac{m_{2}v_{2f}^{2}}{2} \tag{VIII}
\end{gather}
\]
Usando o Princípio da Conservação da Quantidade de Movimento com as equações (I) e (II), antes do
choque, e as equações (V) e (VI), depois do choque
\[
\begin{gather}
Q_{i}=Q_{f}\\
m_{1}v_{1}-m_{2}v_{2}=m_{1}v_{1f}+m_{2}v_{2f} \tag{IX}
\end{gather}
\]
Usando o Princípio da Conservação da Energia com as equações (III) e (IV), antes do choque, e as
equações (VII) e (VIII), depois do choque
\[
\begin{gather}
E_{i}^{c}=E_{f}^{c}\\
\frac{m_{1}v_{1}^{2}}{\cancel{2}}+\frac{m_{2}v_{2}^{2}}{\cancel{2}}=\frac{m_{1}v_{1f}^{2}}{\cancel{2}}+\frac{m_{2}v_{2f}^{2}}{\cancel{2}}\\
m_{1}v_{1}^{2}+m_{2}v_{2}^{2}=m_{1}v_{1f}^{2}+m_{2}v_{2f}^{2} \tag{X}
\end{gather}
\]
As equações (IX) e (X) formam um sistema de duas equações a duas incógnitas
(v1f e v2f)
\[
\left\{
\begin{matrix}
\;m_{1}v_{1}-m_{2}v_{2}=m_{1}v_{1f}+m_{2}v_{2f}\\
\;m_{1}v_{1}^{2}+m_{2}v_{2}^{2}=m_{1}v_{1f}^{2}+m_{2}v_{2f}^{2}
\end{matrix} \tag{XI}
\right.
\]
a) Fazendo v2 = 0 no sistema (XI)
\[
\begin{gather}
\left\{
\begin{matrix}
\;m_{1}v_{1}-m_{2}.0=m_{1}v_{1f}+m_{2}v_{2f}\\
\;m_{1}v_{1}^{2}+m_{2}.0^{2}=m_{1}v_{1f}^{2}+m_{2}v_{2f}^{2}
\end{matrix}
\right.
\\[5pt]
\left\{
\begin{matrix}
\;m_{1}v_{1}=m_{1}v_{1f}+m_{2}v_{2f}\\
\;m_{1}v_{1}^{2}=m_{1}v_{1f}^{2}+m_{2}v_{2f}^{2}
\end{matrix}
\right.
\end{gather}
\]
isolando o valor de v2f na primeira equação
\[
\begin{gather}
m_{2}v_{2f}=m_{1}v_{1}-m_{1}v_{1f}\\
v_{2f}=\frac{1}{m_{2}}(m_{1}v_{1}-m_{1}v_{1f}) \tag{XII}
\end{gather}
\]
e substituindo na segunda
\[
\begin{gather}
m_{1}v_{1}^{2}=m_{1}v_{1f}^{2}+m_{2}\left[\frac{1}{m_{2}}(m_{1}v_{1}-m_{1}v_{1f})\right]^{2}\\
m_{1}v_{1}^{2}=m_{1}v_{1f}^{2}+\cancel{m_{2}}\frac{1}{m_{2}^{\cancel{2}}}(m_{1}v_{1}-m_{1}v_{1f})^{2}
\end{gather}
\]
o termo entre parênteses do lado direito da igualdade é um Produto Notável do tipo
\( (a-b)^{2}=a^{2}-2ab+b^{2} \)
\[
\begin{gather}
m_{1}v_{1}^{2}=m_{1}v_{1f}^{2}+\frac{1}{m_{2}}\left(m_{1}^{2}v_{1}^{2}-2m_{1}^{2}v_{1}v_{1f}+m_{1}^{2}v_{1f}^{2}\right) \tag{XIII}
\end{gather}
\]
multiplicando a equação (XIII) por m2
\[
\begin{gather}
\qquad \qquad \qquad m_{1}v_{1}^{2}=m_{1}v_{1f}^{2}+\frac{1}{m_{2}}\left(m_{1}^{2}v_{1}^{2}-2m_{1}^{2}v_{1}v_{1f}+m_{1}^{2}v_{1f}^{2}\right)\ \ \ \ \ \ \ \ (\;\times m_{2}\;)\\
\; m_{1}m_{2}v_{1}^{2}=m_{1}m_{2}v_{1f}^{2}+m_{1}^{2}v_{1}^{2}-2m_{1}^{2}v_{1}v_{1f}+m_{1}^{2}v_{1f}^{2}\\
\; \cancel{m_{1}}m_{2}v_{1}^{2}=\cancel{m_{1}}\left( m_{2}v_{1f}^{2}+m_{1}v_{1}^{2}-2m_{1}v_{1}v_{1f}+m_{1}v_{1f}^{2}\right)\\
m_{2}v_{1}^{2}=m_{2}v_{1f}^{2}+m_{1}v_{1}^{2}-2m_{1}v_{1}v_{1f}+m_{1}v_{1f}^{2}
\end{gather}
\]
coletando os termos em
\( v_{1f} \)
e
\( v_{1f}^{2} \)
\[
\left(m_{2}+m_{1}\right)v_{1f}^{2}-2m_{1}v_{1}v_{1f}+m_{1}v_{1}^{2}-m_{2}v_{1}^{2}=0
\]
Esta é uma Equação do 2.º Grau do tipo
\( ax^{2}+bx+c=0 \)
onde a incógnita é o valor desejado v1f.
Solução de
\( \underbrace{\left(m_{2}+m_{1}\right)}_{a}\underbrace{v_{1f}^{2}}_{x^{2}}-\underbrace{2m_{1}v_{1}}_{b}\underbrace{v_{1f}}_{x}+\underbrace{m_{1}v_{1}^{2}-m_{2}v_{1}^{2}}_{c}=0 \)
\[ \underbrace{\left(m_{2}+m_{1}\right)}_{a}\underbrace{v_{1f}^{2}}_{x^{2}}-\underbrace{2m_{1}v_{1}}_{b}\underbrace{v_{1f}}_{x}+\underbrace{m_{1}v_{1}^{2}-m_{2}v_{1}^{2}}_{c}=0 \]
\[
\begin{array}{l}
\Delta=b^{2}-4ac=\left(-2m_{1}v_{1}\right)^{2}-4\left(m_{2}+m_{1}\right)\left(m_{1}v_{1}^{2}-m_{2}v_{1}^{2}\right)\\
\Delta=4m_{1}^{2}v_{1}^{2}-4\left(m_{1}m_{2}v_{1}^{2}-m_{2}^{2}v_{1}^{2}+m_{1}^{2}v_{1}^{2}-m_{1}m_{2}v_{1}^{2}\right)\\
\Delta=4m_{1}^{2}v_{1}^{2}-4\left(-m_{2}^{2}v_{1}^{2}+m_{1}^{2}v_{1}^{2}\right)\hfill\\
\Delta=4m_{1}^{2}v_{1}^{2}+4m_{2}^{2}v_{1}^{2}-4m_{1}^{2}v_{1}^{2}\\
\Delta =4m_{2}^{2}v_{1}^{2}\\[10pt]
v_{1f}=\dfrac{-b\pm\sqrt{\Delta \;}}{2a}=\dfrac{-\left(-2m_{1}v_{1}\right)\pm\sqrt{4m_{2}^{2}v_{1}^{2}\;}}{2(m_{1}+m_{2})}\\
v_{1f}=\dfrac{2m_{1}v_{1}\pm2m_{2}v_{1}}{2(m_{1}+m_{2})}\\
v_{1f}=\dfrac{m_{1}v_{1}+m_{2}v_{1}}{(m_{1}+m_{2})}\ \ \ \text{ou}\ \ \ v_{1f}=\dfrac{m_{1}v_{1}-m_{2}v_{1}}{(m_{1}+m_{2})}
\end{array}
\]
\[
\begin{gather}
v_{1f}=\frac{(m_{1}+m_{2})}{(m_{1}+m_{2})}v_{1}\\
v_{1f}=v_{\;1} \tag{XIV}
\end{gather}
\]
\[
\text{ou} \\
\]
\[
v_{1f}=\frac{(m_{1}-m_{2})}{(m_{1}+m_{2})}v_{1}
\]
\[ \bbox[#FFCCCC,10px]
{v_{1f}=\frac{(m_{1}-m_{2})}{(m_{1}+m_{2})}v_{1}}
\]
substituindo esta solução na expressão (XII)
\[
\begin{gather}
v_{2f}=\frac{1}{m_{2}}\left[m_{1}v_{1}-m_{1}\frac{\left(m_{1}-m_{2}\right)}{(m_{1}+m_{2})}v_{1}\right]\\[5pt]
v_{2f}=\frac{1}{m_{2}}\left[\frac{m_{1}v_{1}(m_{1}+m_{2})-m_{1}\left(m_{1}-m_{2}\right)v_{1}}{(m_{1}+m_{2})}\right]\\[5pt]
v_{2f}=\frac{1}{m_{2}}\left[\frac{m_{1}^{2}v_{1}+m_{1}m_{2}v_{1}-m_{1}^{2}v_{1}+m_{1}m_{2}v_{1}}{(m_{1}+m_{2})}\right]\\[5pt]
v_{2f}=\frac{1}{m_{2}}\left[\frac{2m_{1}m_{2}v_{1}}{(m_{1}+m_{2})}\right]\\[5pt]
v_{2}=\frac{m_{2}}{m_{2}}\left[\frac{2m_{1}v_{1}}{(m_{1}+m_{2})}\right]
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{v_{2f}=\frac{2m_{1}v_{1}}{(m_{1}+m_{2})}}
\]
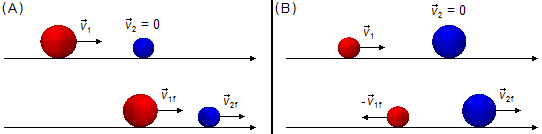
Se m1 > m2, a velocidade final da bola 1 será positiva (v1f > 0), pois m1 − m2 > 0, a velocidade final da bola 2 também será positiva (v2f > 0). Isto significa que após o choque a bola 1 continua se deslocando no mesmo sentido da trajetória com velocidade menor e a bola 2, que estava em repouso, começa a se deslocar no mesmo sentido (Figura 2-A).
Se m1 < m2, a velocidade final da bola 1 será negativa (v1f < 0), pois m1 − m2 < 0, a velocidade final da bola 2 será positiva (v2f > 0). Isto significa que a bola 1 que se deslocava no mesmo sentido da trajetória inverte seu movimento após o choque e volta contra a orientação da trajetória, a bola 2 começa a se deslocar favor da orientação da trajetória (Figura 2-B).
Substituindo a solução (XIV) na expressão (XII)
\[
\begin{gather}
v_{2f}=\frac{1}{m_{2}}(m_{1}v_{1}-m_{1}v_{1})\\
v_{2f}=\frac{1}{m_{2}}.0\\
v_{2f}=0 \tag{XV}
\end{gather}
\]
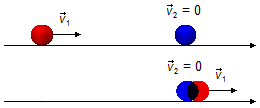
Observação: As soluções (XIV) e (XV) não foram utilizadas, pois, apresentam uma impossibilidade física.
A bola 1 continuaria com sua velocidade a favor da orientação da trajetória e a bola 2 continuaria em repouso, não
haveria choque, a bola 1 seria uma “bola fantasma” passando uma através da bola 2 (Figura 3).
b) Fazendo m1 = m2 = m no sistema (XI)
\[
\begin{gather}
\left\{
\begin{matrix}
\;\cancel{m}v_{1}-\cancel{m}v_{2}=\cancel{m}v_{1f}+\cancel{m}v_{2f}\\
\;\cancel{m}v_{1}^{2}+\cancel{m}v_{2}^{2}=\cancel{m}v_{1f}^{2}+\cancel{m}v_{2f}^{2}
\end{matrix}
\right.
\\[5pt]
\left\{
\begin{matrix}
\;v_{1}-v_{2}=v_{1f}+v_{2f}\\
\;v_{1}^{2}+v_{2}^{2}=v_{1f}^{2}+v_{2f}^{2}
\end{matrix}
\right.
\end{gather}
\]
isolando o valor de v2f na primeira equação
\[
\begin{gather}
v_{2f}=v_{1}-v_{2}-v_{1f} \tag{XVI}
\end{gather}
\]
e substituindo na segunda equação
\[
v_{1}^{2}+v_{2}^{2}=v_{1f}^{2}+(v_{1}-v_{2}-v_{1f})^{2}
\]
o termo entre parênteses do lado direito da igualdade é do tipo
\( (a-b-c)^{2}=a^{2}+b^{2}+c^{2}-2ab-2ac+2bc \)
\( (a-b-c)^{2}=a^{2}+b^{2}+c^{2}-2ab-2ac+2bc \)
aplicando à expressão acima
\[
v_{1}^{2}+v_{2}^{2}=v_{1f}^{2}+v_{1}^{2}-2v_{1}v_{2}-2v_{1}v_{1f}+v_{2}^{2}+2v_{2}v_{1f}+v_{1f}^{2}
\]
Observação: Na dúvida podemos multiplicar diretamente os dois termos
\[
\begin{array}{l}
\begin{array}{l}
v_{1}-v_{2}-v_{1f}\\
v_{1}-v_{2}-v_{1f}
\end{array}\\
\hline
\begin{alignat}{4}
& v_{1}^{2} & - & v_{1}v_{2} & - & v_{1}v_{1f}\\
& & - & v_{1}v_{2} & & & + & v_{2}^{2} & + & v_{2}v_{1f}\\
& & & & - & v_{1}v_{1f} & & & + & v_{2}v_{1f} & + & v_{1f}^{2}\\
\hline
& v_{1}^{2} & - & 2 v_{1}v_{2} & - & 2 v_{1}v_{1f} & + & v_{2}^{2} & + & 2 v_{2}v_{1f} & + & v_{1f}^{2}
\end{alignat}\\
\end{array}
\]
\[
\begin{gather}
\cancel{v_{1}^{2}}+\cancel{v_{2}^{2}}=\cancel{v_{1}^{2}}-2v_{1}v_{2}-2v_{1}v_{1f}+\cancel{v_{2}^{2}}+2v_{2}v_{1f}+v_{1f}^{2}\\
0=v_{1f}^{\;2}-2v_{1}v_{2}-2v_{1}v_{1f}+2v_{2}v_{1f}+v_{1f}^{2}
\end{gather}
\]
coletando os termos em
\( v_{1f} \)
e
\( v_{1f}^{2} \)
\[
2v_{1f}^{;2}+\left(2v_{2}-2v_{1}\right)v_{1f}-2v_{1}v_{2}=0
\]
Esta é uma Equação do 2.º Grau do tipo
\( ax^{2}+bx+c=0 \)
onde a incógnita é o valor desejado v1f.
Solução de
\( \underbrace{2}_{a}\underbrace{v_{1f}^{2}}_{x^{2}}+\underbrace{\left(2v_{2}-2v_{1}\right)}_{b}\underbrace{v_{1f}}_{x}-\underbrace{2v_{1}v_{2}}_{c}=0 \)
\( \underbrace{2}_{a}\underbrace{v_{1f}^{2}}_{x^{2}}+\underbrace{\left(2v_{2}-2v_{1}\right)}_{b}\underbrace{v_{1f}}_{x}-\underbrace{2v_{1}v_{2}}_{c}=0 \)
\[
\begin{array}{l}
\Delta=b^{2}-4ac=\left(2v_{2}-2v_{1}\right)^{2}-4.2\left(-2v_{1}v_{2}\;\right)\\
\Delta=4v_{2}^{2}-8v_{1}v_{2}+4v_{1}^{2}-8\left(-2v_{1}v_{2}\right)\\
\Delta =4v_{1}^{2}-8v_{1}v_{2}+4v_{2}^{2}+16v_{1}v_{2}\\
\Delta=4v_{1}^{2}+8v_{1}v_{2}+4v_{2}^{2}\\
\Delta=4\left(v_{1}^{2}+2v_{1}v_{2}+v_{2}^{2}\right)
\end{array}
\]
o termo entre parênteses é um Produto Notável do tipo
\( (a^{2}+2ab+b^{2})=(a+b)^{2} \)
\[
\begin{gather}
\Delta =4\left(v_{1}+v_{2}\right)^{2} \qquad\qquad\qquad\qquad\qquad\qquad
\\{\,}\\
v_{1f}=\frac{-b\pm \sqrt{\Delta
}}{2a}=\frac{-\left(2v_{2}-2v_{1}\right)\pm \sqrt{4\left(v_{1}+v_{2}\right)^{2}}}{2.2}\\
v_{1f}=\frac{2\left(v_{1}-v_{2}\right)\pm 2\left(v_{1}+v_{2}\right)}{2.2}\\
v_{1f}=\frac{v_{1}-v_{2}+(v_{1}+v_{2})}{2}\ \ \ \text{ou}\ \ \ v_{1f}=\frac{v_{1}-v_{2}-(v_{1}+v_{2})}{2}\\
v_{1f}=\frac{v_{1}-v_{2}+v_{1}+v_{2}}{2}\ \ \ \text{ou}\ \ \ v_{1f}=\frac{v_{1}-v_{2}-v_{1}-v_{2}}{2}\\
v_{1f}=\frac{2}{2}v_{\;1}\ \ \ \text{ou}\ \ \ v_{1f}=\frac{-{2}}{2}v_{\;2}
\end{gather}
\]
\[
\begin{gather}
v_{1f}=v_{1} \tag{XVII}
\end{gather}
\]
\[
\text{ou}
\]
\[ \bbox[#FFCCCC,10px]
{v_{1f}=-v_{2}}
\]
substituindo esta solução na expressão (XVI)
\[
\begin{gather}
v_{2f}=v_{1}-v_{2}-(-v_{2})\\
v_{2f}=v_{1}-v_{2}+v_{2}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{v_{2f}=v_{1}}
\]
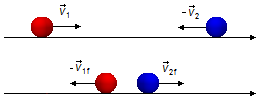
Neste caso as bolas “trocam” suas velocidades, a bola 1 volta contra a orientação da trajetória com o
módulo da sua velocidade igual ao módulo da velocidade da bola 2, enquanto a bola 2 volta a favor da
trajetória com o módulo da sua velocidade igual ao módulo da velocidade da bola 1 (Figura 4).
Substituindo a solução (XVII) na expressão (XVI)
\[
\begin{gather}
v_{2f}=v_{1}-v_{2}-v_{1}\\
v_{2f}=-v_{2} \tag{XVIII}
\end{gather}
\]
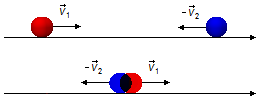
Observação: As soluções (XVII) e (XVIII) não foram utilizadas, pois, apresentam uma impossibilidade
física. A bola 1 continuaria com sua velocidade a favor da orientação da trajetória e a bola 2 continuaria com
sua velocidade contra a orientação da trajetória, não haveria choque, seriam duas “bolas fantasmas” passando uma
através da outra (Figura 5).
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .