Solved Problem on Dynamics
advertisement   



An Atwood machine has masses, of mA = 6.25 kg and mB = 6.75 kg, connected by a weightless cord through a pulley frictionless. Find:
a) The acceleration of the system;
b) The tension in the rope connecting the masses;
c) The tension in the rope that holds the system to the ceiling.


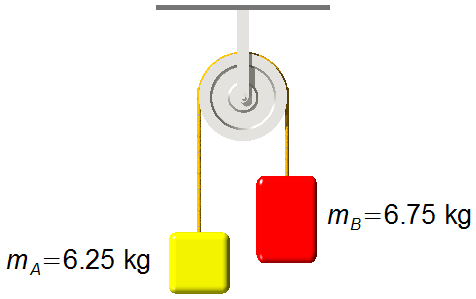
Problem data:
  • Mass of body A:    mA = 6.25 kg;
  • Mass of body B:    mB = 6.75 kg;
  • Acceleration due to gravity:    g = 9.8 m/s2.
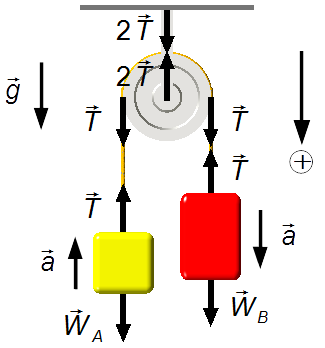
Problem diagram:

Since the mass of block B is greater than the mass of block A, block B drops while block A rises. As the cord has a negligible mass and the pulley is frictionless, the acceleration is the same for the whole system.
We consider a frame of reference oriented positively, in the direction of block B moves downward, in the same direction of the acceleration due to gravity.
As the rope has a negligible mass, it only transmits the tension from one side to the other side of the pulley between blocks (Figure 1).
Figure 1

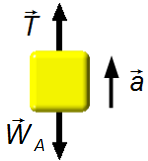
Drawing a free-body diagram for each block.

  • Body A (Figure 2):
    • \( \vec T \) : tension force on the rope;
    • \( {\vec W}_{\small A} \) : weight of block A.
Figure 2

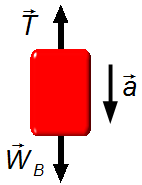
  • Body B (Figure3 ):
    • \( \vec T \) : tension on the cord;
    • \( {\vec W}_{\small B} \) : weight of block B.
Figure 3

Solution

Applying Newton's Second Law
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Body A:
\[ \begin{gather} T-W_{\small A}=m_{\small A}a \tag{I} \end{gather} \]
  • Body B:
\[ \begin{gather} W_{\small B}-T=m_{\small B}a \tag{II} \end{gather} \]
The weight is given by
\[ \begin{gather} \bbox[#99CCFF,10px] {W=m g} \end{gather} \]
weight of bodies A and B
\[ \begin{gather} W_{\small A}=m_{\small A}g \tag{III-a} \end{gather} \]
\[ \begin{gather} W_{\small B}=m_{\small B}g \tag{III-b} \end{gather} \]
substituting the equation (III-a) into equation (I)
\[ \begin{gather} T-m_{\small A}g=m_{\small A}a \tag{IV} \end{gather} \]
substituting the expression (III-b) into expression (II)
\[ \begin{gather} m_{\small B}g-T=m_{\small B}a\tag{V} \end{gather} \]
Equations (IV) and (V) can be written as a system of linear equations with two variables (a and T), adding the two equations
\[ \begin{gather} \frac{ \left\{ \begin{array}{rr} \cancel{T}-m_{\small A}g=m_{\small A}a\\ m_{\small B}g-\cancel{T}=m_{\small B}a \end{array} \right.} {(m_{\small B}-m_{\small A})g=(m_{\small B}+m_{\small A})a}\\[6pt] a=\frac{(m_{\small B}-m_{\small A})g}{(m_{\small B}+m_{\small A})}\\[6pt] a=\frac{(6.75-6.25)\;\mathrm{\cancel{kg}}\times 9.8\;\mathrm{m/s^2}}{(6.75+6.25)\;\mathrm{\cancel{kg}}} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a\approx 0.38\;\mathrm{m/s^2}} \end{gather} \]

b) Substituting the value found in item (a) in the first (or second equation of the system), we obtain the tension in the rope
\[ \begin{gather} T-m_{\small A}g=m_{\small A}a\\[5pt] T=(6.25\;\mathrm{kg})\times(9.8\;\mathrm{m/s^2})+(6.25\;\mathrm{kg})\times(0.38\;\mathrm{m/s^2}) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T\approx 63.63\;\mathrm N} \end{gather} \]

c) Since the pulley distributes the tension equally in the rope on both sides of the pulley, the tension in the rope that supports the system in the roof will be double (Figure 1)
\[ \begin{gather} 2T=2\times 63.63\;\mathrm N \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {2T\approx 127.26\;\mathrm N} \end{gather} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .