Exercício Resolvido de Regiões do Plano Complexo
publicidade
b) \( \displaystyle |z-i|+|z+i| \lt 4 \)s
Sendo z = x+iy
\[
\begin{gather}
|x+iy-i|+|x+iy+i| \lt 4\\
|x+i(y-1)|+|x+i(y+1)| \lt 4\\
|x+i(y-1)| \lt 4-|x+i(y+1)|
\end{gather}
\]
elevando ambos os lados da igualdade ao quadrado
\[
(|x+i(y-1)|)^{2} \lt (4-|x+i(y+1)|)^{2}
\]
Lembrando que para z = a+bi
\[
\begin{gather}
|z|^{2}=a^{2}+b^{2}\\
|z|=\sqrt{a^{2}+b^{2}}
\end{gather}
\]
\[
\begin{gather}
|x^{2}+i(y-1)|^{2} \lt 4^{2}-2.4|x+i(y+1)|+|x+i(y+1)|^{2}\\
x^{2}+(y-1)^{2} \lt 16-8\sqrt{x^{2}+(y+1)^{2}}+x^{2}+(y+1)^{2}\\
(y-1)^{2} \lt 16-8\sqrt{x^{2}+(y+1)^{2}}+(y+1)^{2}\\
y^{2}-2y+1 \lt 16-8\sqrt{x^{2}+(y+1)^{2}}+y^{2}+2y+1\\
-2y \lt 16-8\sqrt{x^{2}+(y+1)^{2}}+2y\\
16+4y \gt 8\sqrt{x^{2}+(y+1)^{2}}\\
4+y \gt 2\sqrt{x^{2}+(y+1)^{2}}
\end{gather}
\]
novamente elevando ambos os lados ao quadrado
\[
\begin{gather}
(4+y)^{2} \gt (2\sqrt{x^{2}+(y+1)^{2}})^{2}\\
16+8y+y^{2} \gt 4(x^{2}+y^{2}+2y+1)\\
16+8y+y^{2} \gt 4x^{2}+4y^{2}+8y+4\\
4x^{2}+4y^{2}-y^{2} \lt 16-4\\
4x^{2}+3y^{2} \lt 12
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\frac{x^{2}}{3}+\frac{y^{2}}{4} \lt 1}
\]
A equação
\( \frac{x^{2}}{3}+\frac{y^{2}}{4}=1 \)
representa uma elipse com focos sobre o eixo-y, semieixo menor igual a
\( \sqrt{3} \)
e semieixo maior igual a 2. Como queremos os pontos para os quais a função tenha valor menor que 1
(<1), isto representa o interior da elipse exlcuindo os pontos da borda (Gráfico 1).
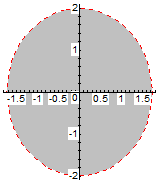
Gráfico 1
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .