Exercício Resolvido de Funções Complexas
publicidade
a) \( \displaystyle 2^{i} \)
Usando a expressão
\[ \bbox[#99CCFF,10px]
{u^{v}=\operatorname{e}^{v\;\text{Ln}u}}
\]
\[
\begin{gather}
2^{i}=\operatorname{e}^{i\;\text{Ln}2} \tag{I}
\end{gather}
\]
A função multivalente do logaritmo é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\operatorname{Ln}z=\ln |z|+i(\operatorname{arg}(z)+2k\pi)} \tag{II}
\end{gather}
\]
O argumento do logaritmo é o número complexo da forma
\[
u=2+0i
\]
O módulo é dado por
\[ \bbox[#99CCFF,10px]
{|z|=\sqrt{x^{2}+y^{2}}}
\]
\[
\begin{gather}
|u|=\sqrt{2^{2}+0^{2}\;}\\
|u|=2 \tag{III}
\end{gather}
\]
O argumento é dado por
\[ \bbox[#99CCFF,10px]
{\theta=\operatorname{arg}(z)=\operatorname{arctg}\left(\frac{y}{x}\right)}
\]
\[
\begin{align}
\theta &=\operatorname{arg}(u)=\operatorname{arctg}\left(\frac{y}{x}\right)=\\
&=\operatorname{arctg}\left(\frac{0}{2}\right)=\operatorname{arctg}(0)=0 \tag{IV}
\end{align}
\]
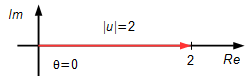
substituindo os valores (III) e (IV) na expressão (II)
\[
\begin{gather}
\operatorname{Ln}(2)=\ln (2)+i(0+2k\pi)\\
\operatorname{Ln}(2)=\ln (2)+2k\pi i \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (I)
\[
\begin{gather}
2^{i}=\operatorname{e}^{i\;\left(\ln (2)+2k\pi i\right)}\\[5pt]
2^{i}=\operatorname{e}^{i\;\ln (2)+2k\pi i.i}\\[5pt]
2^{i}=\operatorname{e}^{i\;\ln (2)+2k\pi i^{2}}\\[5pt]
2^{i}=\operatorname{e}^{i\;\ln (2)+2k\pi(-1)}\\[5pt]
2^{i}=\operatorname{e}^{i\;\ln (2)-2k\pi}
\end{gather}
\]
\[
\qquad \qquad \quad 2^{i}=\operatorname{e}^{i\;\ln (2)+2k\pi}\quad ,\quad k\in \mathbb{Z}
\]
\[
\begin{gather}
2^{i}=\operatorname{e}^{i\;\ln (2)+2k\pi}\\[5pt]
2^{i}=\operatorname{e}^{i\;\ln (2)}.\operatorname{e}^{2k\pi}
\end{gather}
\]
Aplicando a Fórmula de Euler
\[ \bbox[#99CCFF,10px]
{\operatorname{e}^{i\theta}=\cos \theta +i\operatorname{sen}\theta}
\]
\[ \bbox[#FFCCCC,10px]
{2^{i}=\operatorname{e}^{2k\pi}\;\left[\cos (\ln(2))+i\operatorname{sen}(\ln(2))\right]}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .