Exercício Resolvido de Números Complexos
publicidade
c) \( \sqrt[{3}]{i} \)
As raízes de um número complexo são dadas por
\[ \bbox[#99CCFF,10px]
{z=\sqrt[{n}]{r}\left(\cos \frac{\theta +2k\pi}{n}+i\operatorname{sen}\frac{\theta +2k\pi }{n}\right)}
\]
\[
\begin{gather}
x+iy=0+i\\[5pt]
r=\sqrt{0^{2}+1^{2}\;}=\sqrt{1\;}=1
\end{gather}
\]
\[
\begin{gather}
\theta=\operatorname{arctg}\left(\frac{1}{0}\right)=\operatorname{arctg}\left(\infty\right)=\frac{\pi }{2}
\end{gather}
\]
Para a raiz cúbica, n=3 e k=0, 1, 2.
Para k=0:
\[
\begin{gathered}
z_{1}=\sqrt[{3}]{1}\left(\cos \frac{\frac{\pi}{2}+2.0\pi }{3}+i\operatorname{sen}\frac{\frac{\pi }{2}+2.0\pi}{3}\right)\\
z_{1}=1\left(\cos \frac{\pi}{6}+i\operatorname{sen}\frac{\pi}{6}\right)\\
z_{1}=1\left(\frac{\sqrt{3}}{2}+i\frac{1}{2}\right)
\end{gathered}
\]
\[ \bbox[#FFCCCC,10px]
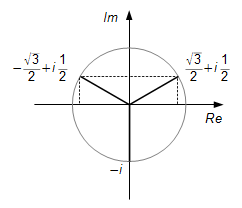
{z_{1}=\frac{\sqrt{3}}{2}+i\frac{1}{2}}
\]
Para k=1:
\[
\begin{gathered}
z_{2}=\sqrt[{3}]{1}\left(\cos \frac{\frac{\pi}{2}+2.1\pi }{3}+i\operatorname{sen}\frac{\frac{\pi }{2}+2.1\pi}{3}\right)\\
z_{2}=1\left(\cos \frac{\frac{\pi +4\pi}{2}}{3}+i\operatorname{sen}\frac{\frac{\pi +4\pi}{2}}{3}\right)\\
z_{2}=1\left(\cos \frac{5\pi}{6}+i\operatorname{sen}\frac{5\pi}{6}\right)\\
z_{2}=1\left(-{\frac{\sqrt{3}}{2}}+i\frac{1}{2}\right)
\end{gathered}
\]
\[ \bbox[#FFCCCC,10px]
{z_{2}=-{\frac{\sqrt{3}}{2}}+i\frac{1}{2}}
\]
Para k=2:
\[
\begin{gathered}
z_{3}=\sqrt[{3}]{1}\left(\cos \frac{\frac{\pi}{2}+2.2\pi }{3}+i\operatorname{sen}\frac{\frac{\pi }{2}+2.2\pi}{3}\right)\\
z_{3}=1\left(\cos \frac{\frac{\pi +8\pi}{2}}{3}+i\operatorname{sen}\frac{\frac{\pi +8\pi}{2}}{3}\right)\\
z_{3}=1\left(\cos \frac{9\pi}{6}+i\operatorname{sen}\frac{9\pi}{6}\right)\\
z_{3}=1\left(0-i\right)
\end{gathered}
\]
\[ \bbox[#FFCCCC,10px]
{z_{3}=-i}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .