Exercício Resolvido de Números Complexos
publicidade
h) \( \displaystyle z=\frac{-4}{\sqrt{3}-i} \)
Multiplicando o numerador e o denominador pelo complexo conjugado do denominador \( \left(\overline{{z}}=\sqrt{3}+i\right) \)
\[
\begin{gather}
z=\frac{-4}{(\sqrt{3}-i)}.\frac{(\sqrt{3}+i)}{(\sqrt{3}+i)}\\[5pt]
z=\frac{-4(\sqrt{3}+i)}{(\sqrt{3}).(\sqrt{3})+\sqrt{3}i-i\sqrt{3}-i.i}\\[5pt]
z=\frac{-4(\sqrt{3}+i)}{(\sqrt{3})^{2}+i\sqrt{3}-i\sqrt{3}-i^{2}}
\end{gather}
\]
sendo
\( i^{2}=-1 \)
\[
\begin{gather}
z=\frac{-4(\sqrt{3}+i)}{3-(-1)}\\[5pt]
z=\frac{-4(\sqrt{3}+i)}{3+1}\\[5pt]
z=\frac{-4(\sqrt{3}+i)}{4}\\[5pt]
z=-\sqrt{3}-i
\end{gather}
\]
O módulo é dado por
\[ \bbox[#99CCFF,10px]
{|z|=\sqrt{x^{2}+y^{2}}}
\]
\[
\begin{gather}
|z|=\sqrt{\left(-\sqrt{3}\right)^{2}+(-1)^{2}}\\[5pt]
|z|=\sqrt{3+1}\\[5pt]
|z|=\sqrt{4}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{|z|=2}
\]
O argumento é dado por
\[ \bbox[#99CCFF,10px]
{\theta=\operatorname{arg}(z)=\operatorname{arctg}\left(\frac{y}{x}\right)}
\]
\[
\begin{gather}
\theta=\operatorname{arctg}\left[\frac{-1}{-\sqrt{3}}\right]\\[5pt]
\theta=\operatorname{arctg}\left[\frac{1}{\sqrt{3}}.\frac{\sqrt{3}}{\sqrt{3}}\right]\\[5pt]
\theta=\operatorname{arctg}\left(\frac{\sqrt{3}}{3}\right)
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
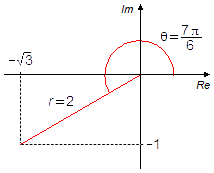
{\theta =\frac{7\pi}{6}}
\]
Escrevendo z na forma polar
\[ \bbox[#99CCFF,10px]
{z=r(\cos \theta +i\operatorname{sen}\theta )\quad \text{,}\quad r=|z|}
\]
\[ \bbox[#FFCCCC,10px]
{z=2\;\left(\cos \frac{7\pi}{6}+i\operatorname{sen}\frac{7\pi}{6}\right)}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .