Exercício Resolvido de Calor e Primeira Lei da Termodinâmica
publicidade
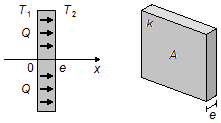
a) Uma parede plana de área A e espessura e é construída com um material de condutividade térmica (k), ela está mantida com temperaturas T1 e T2 nos seus lados externo e interno respectivamente (T1 > T2). Determine a quantidade de calor por unidade de tempo conduzida do exterior para o interior, através da parede, no estado estacionário.
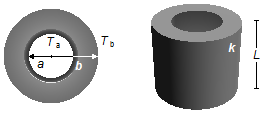
b) Um tubo cilíndrico possui raio interno a e raio externo b, o tubo tem um comprimento L e é construído de um material de condutividade térmica (k). O interior do tubo é mantido a uma temperatura Ta e seu exterior está a uma temperatura Tb (Ta > Tb). Determine a quantidade de calor por unidade de tempo conduzida do interior para o exterior do tubo no estado estacionário.
Solução
a) O fluxo de calor é dado pela quantidade de calor por unidade de área e por unidade de tempo
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\phi =\frac{Q}{A\Delta t}} \tag{I}
\end{gather}
\]
Pela Lei da Condução Térmica ou Lei de Fourier o fluxo de calor é proporcional ao gradiente negativo
da temperatura
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\phi =-k\frac{dT}{dr}} \tag{II}
\end{gather}
\]
onde a constante de proporcionalidade é a condutividade térmica do material (k).Igualando as expressões (I) e (II)
\[
\begin{gather}
\frac{Q}{A\Delta t}=-k\frac{dT}{dr} \tag{III}
\end{gather}
\]
Na parede o calor se propaga na direção x, temos
\( dr=dx \)
(Figura 1). Separando as variáveis na expressão (III)
\[
\frac{Q}{\Delta t}dx=-kAdT
\]
integrando de ambos os lados da igualdade
\[
\int {{\frac{Q}{\Delta t}dx}}=\int {{-kAdT}}
\]
\[
\frac{Q}{\Delta t}\int _{0}^{e}{{dx}}=-kA\;\int _{T_{1}}^{T_{2}}{{dT}}
\]
Integração de \( \displaystyle \int_{0}^{e}{{dx}} \)
\[
\int _{0}^{e}{{dx}}=\left.x\;\right|_{\;0}^{\;e}=e-0=e
\]
Integração de \( \displaystyle \int_{T_{1}}^{T_{2}}{{dT}} \)
\[
\int_{T_{1}}^{T_{2}}{{dT}}=\left.T\;\right|_{\;T_{1}}^{\;T_{2}}=T_{2}-T_{1}
\]
\[
\begin{gather}
\frac{Q}{\Delta t}e=-kA\left(T_{2}-T_{1}\right)\\
\frac{Q}{\Delta t}=-kA\frac{\left(T_{2}-T_{1}\right)}{e}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\frac{Q}{\Delta t}=kA\frac{\left(T_{1}-T_{2}\right)}{e}}
\]
b) A área A de uma casca cilíndrica de raio r e comprimento L é dada por (Figura 2)
\[
\begin{gather}
A=2\pi rL \tag{IV}
\end{gather}
\]

\[
\frac{Q}{2\pi rL\Delta t}=-k\frac{dT}{dr}
\]
Separando as variáveis na expressão
\[
\frac{Q}{r\Delta t}dr=-2\pi kLdT
\]
integrando de ambos os lados da igualdade
\[
\int {{\frac{Q}{\Delta t}\frac{dr}{r}}}=\int {{-2\pi kLdT}}
\]
\[
\frac{Q}{\Delta t}\int _{a}^{b}{{\frac{dr}{r}}}=-2\pi kL\int_{T_{1}}^{T_{2}}{{dT}}
\]
Integração de \( \displaystyle \int_{a}^{b}{{\dfrac{dr}{r}}} \)
\[
\int _{a}^{b}{{\frac{dr}{r}}}=\left.\ln r\;\right|_{\;a}^{\;b}=\ln b-\ln a=\ln \frac{b}{a}
\]
a integral em dT já foi obtida no item (a).
\[
\begin{gather}
\frac{Q}{\Delta t}\ln \frac{b}{a}=-2\pi kL\left(T_{2}-T_{1}\right)\\
\frac{Q}{\Delta t}=-2\pi kL\frac{\left(T_{2}-T_{1}\right)}{\ln \dfrac{b}{a}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\frac{Q}{\Delta t}=2\pi kL\frac{\left(T_{1}-T_{2}\right)}{\ln \dfrac{b}{a}}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .