Exercício Resolvido de Radiação de Corpo Negro
Português
English
publicidade
Um radiador de cavidade a 6000 K tem um orifício de 0,10 mm de diâmetro feito em sua parede. Ache a potência irradiada através do orifício no intervalo de comprimentos de onda de 5500 Å a 5510 Å.
Dados do problema:
- Temperatura da cavidade: T = 6000 K;
- Diâmetro do orifício: d = 0,10 mm;
- Comprimento de onda mínima: λ1 = 5500 Å;
- Comprimento de onda máxima: λ2 = 5510 Å.
- Velocidade da luz: c = 2,998.108 m/s;
- Constante de Planck: h = 6,63.10--34 J.s;
- Constante de Boltzmann: k = 1,38.10--23 J/K.
a) A radiância total é definida como a potência irradiada por unidade de área
\[
\begin{gather}
R_{T}=\frac{P}{A}
\end{gather}
\]
a integral da radiância sobre todas as frequências fornece a potência irradiada
\[
\begin{gather}
P=A\int {}R_{T}(\nu)\;d\nu \tag{I}
\end{gather}
\]
A relação entre a radiância espectral e a densidade de energia é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{T}(\nu)=\frac{c}{4}\rho (\nu)} \tag{II}
\end{gather}
\]
substituindo a expressão (II) na expressão (I) e integrando no intervalo de frequências do problema
\[
\begin{gather}
P=A\int_{\nu_{1}}^{\nu_{2}}{}\frac{c}{4}\rho (\nu)\;d\nu \\[5pt]
P=\frac{Ac}{4}\int_{\nu_{1}}^{\nu_{2}}{}\rho (\nu)\;d\nu \tag{III}
\end{gather}
\]
a Lei da Radiação de Planck para a densidade de energia é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\rho (\nu)\;d\nu =\frac{8\pi \nu^{3}}{c^{3}}\frac{h}{\operatorname{e}^{h\nu/{kT}}-1}\;d\nu} \tag{IV}
\end{gather}
\]
A relação entre a densidade de energia, em função da frequência, e da energia, em função do comprimento de
onda, é dada por
\[
\begin{gather}
\rho_{T}(\lambda )=-\rho_{T}(\nu)\;\frac{d\nu }{d\lambda } \tag{V}
\end{gather}
\]
A frequência é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\nu =\frac{c}{\lambda}} \tag{VI}
\end{gather}
\]
a derivada da frequência em relação ao comprimento de onda é dada por
\[
\begin{gather}
\frac{d\nu}{d\lambda}=\frac{d(c\lambda^{-1})}{d\lambda}=-c\lambda^{-2}=-{\frac{c}{\lambda^{2}}} \tag{VII}
\end{gather}
\]
substituindo as expressões (IV), (VI) e (VII) na expressão (V)
\[
\begin{gathered}
\rho_{T}(\lambda)=-\left[\frac{8\pi}{c^{3}}\left(\frac{c}{\lambda}\right)^{3}\frac{h}{\operatorname{e}^{hc/{kT\lambda}}-1}\right]\;\left(-{\frac{c}{\lambda^{2}}\;d\lambda}\right)\\[5pt]
\rho_{T}(\lambda)=\frac{8\pi c^{3}}{c^{3}\lambda^{3}}\frac{c}{\lambda^{2}}\frac{h}{\operatorname{e}^{hc/{kT\lambda}}-1}\;d\lambda
\end{gathered}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\rho_{T}(\lambda)\;d\lambda =\frac{8\pi c}{\lambda^{5}}\frac{h}{\operatorname{e}^{hc/{kT\lambda }}-1}\;d\lambda}
\end{gather}
\]
A expressão (III) pode ser escrita como
\[
\begin{gather}
P=\frac{Ac}{4}\int_{\lambda_{1}}^{\lambda_{2}}{}\frac{8\pi c}{\lambda ^{5}}\frac{h}{\operatorname{e}^{hc/{kT\lambda}}-1}\;d\lambda
\end{gather}
\]
Observação: Não precisamos calcular a integral, podemos aproximar o valor usando o
Teorema do Valor Médio para Integrais.
A integral de uma função f(x) em um intervalo [a, b] representa a área sob a curva (Figura 1), pelo Teorema do Valor Médio para Integrais temos um valor f(c) da função que determina um retângulo com base igual ao comprimento do intervalo e altura f(c) (Figura 2).
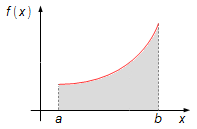Figura 1
Figura 2
O ponto c está localizado em um lugar qualquer do intervalo [a, b], de tal forma que
o valor f(c) nos dê áreas iguais sob as curvas.
Em particular se a função f(x) for linear o ponto c está no ponto médio do intervalo [a, b] (Figura 3). Isso acontece porque as áreas acima e abaixo do valor de f(c) se compensam.
Figura 3
No problema a diferença de comprimentos de onda em relação aos valores dados é
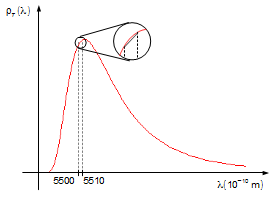Figura 4
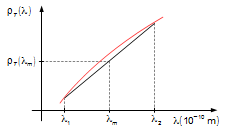Figura 5
A integral de uma função f(x) em um intervalo [a, b] representa a área sob a curva (Figura 1), pelo Teorema do Valor Médio para Integrais temos um valor f(c) da função que determina um retângulo com base igual ao comprimento do intervalo e altura f(c) (Figura 2).
Em particular se a função f(x) for linear o ponto c está no ponto médio do intervalo [a, b] (Figura 3). Isso acontece porque as áreas acima e abaixo do valor de f(c) se compensam.
No problema a diferença de comprimentos de onda em relação aos valores dados é
\[
\begin{gather}
\frac{\Delta \lambda }{\lambda _{1}}=\frac{\lambda _{2}-\lambda_{1}}{\lambda_{1}}=\frac{5510.10^{-10}-5500.10^{-10}}{5500.10^{-10}}=0,002
\end{gather}
\]
\[
\begin{gather}
\frac{\Delta \lambda }{\lambda _{2}}=\frac{\lambda _{2}-\lambda_{2}}{\lambda_{1}}=\frac{5510.10^{-10}-5500.10^{-10}}{5510.10^{-10}}=0,002
\end{gather}
\]
vemos que a variação no intervalo de comprimentos de onda varia de 2 partes por 1000, este intervalo é
pequeno (Figura 4), podemos aproximar o intervalo infinitesimal de comprimentos de onda, dλ,
pelo intervalo, Δλ, e a variável de integração, λ, pode ser substituída
pelo seu valor médio, λm (Figura 5).
Podemos substituit a integral para a potência pela seguinte expressão
\[
\begin{gathered}
P=\frac{Ac}{4}\frac{8\pi c}{\lambda_{m}^{5}}\frac{h}{\operatorname{e}^{hc/{kT\lambda_{m}}}-1}\;\Delta \lambda \\[5pt]
P=\frac{2A\pi c^{2}}{\lambda_{m}^{5}}\frac{h}{\operatorname{e}^{hc/{kT\lambda_{m}}}-1}\;\Delta \lambda
\end{gathered}
\]
Substituindo a variável de integração λ pelo valor médio do intervalo de comprimentos de onda
\[
\begin{gathered}
\lambda_{m}=\frac{\lambda_{1}+\lambda_{2}}{2}\\[5pt]
\lambda_{m}=\frac{5500.10^{-10}+5510.10^{-10}}{2}\\[5pt]
\lambda_{m}=\frac{11010.10^{-10}}{2}\\[5pt]
\lambda_{m}=5505.10^{-10}\;\overset{\circ}{\text{A}}
\end{gathered}
\]
e substituindo o intervalo diferencial dλ pelo intervalo Δλ dado por
\[
\begin{gathered}
\Delta \lambda =\lambda_{1}-\lambda_{2}\\[5pt]
\Delta\lambda =5510.10^{-10}-5500.10^{-10}\\[5pt]
\Delta \lambda=10.10^{-10}\;\overset{\circ}{\text{A}}
\end{gathered}
\]
A área do orifício será
\[
\begin{gathered}
A=\pi r^{2}\\
A=\pi\left(\frac{d}{2}\right)^{2}\\[5pt]
A=3,14.\left(\frac{10.10^{-3}}{2}\right)^{2}\\[5pt]
A=7,85.10^{-5}\;\text{m}^{2}
\end{gathered}
\]
substituindo os dados
\[
\begin{align}
P=& \frac{2.(7,85.10^{-5}).3,14.(2,998.10^{8})^{2}}{(5505.10^{-10})^{5}}\times\\
&\times{\frac{(6,63.10^{-34})}{\operatorname{e}^{(6,63.10^{-34}).(2,998.10^{8})/{[(1,38.10^{-23}).(6000).5505.10^{-10}]}}-1}.(10.10^{-10})}\;\Delta\lambda\\[5pt]
&\qquad \qquad \quad P=\frac{4,43.10^{13}}{5,06.10^{-32}}.\frac{6,63.10^{-34}}{\operatorname{e}^{4,36}-1}.(10.10^{-10})\\[5pt]
&\qquad \qquad \qquad P=8,75.10^{44}.8,58.10^{-36}.10.10^{-10}
\end{align}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{P=7,5\;\text{W}}
\end{gather}
\]
publicidade
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .