Exercício Resolvido de Centro de Massa e Quantidade de Movimento

Uma partícula de massa m₁ e velocidade v_1i colide com outra partícula de massa m₂ em repouso, o choque não se dá frontalmente. Determinar as velocidades das partículas após o choque em função dos ângulos de espalhamento.

Dados do problema:

Massa da partícula 1: m₁;
Velocidade inicial da partícula 1: v_1i;
Ângulo de espalhamento da partícula 1: θ₁;
Massa da partícula 2: m₂;
Velocidade inicial da partícula 2: v_2i = 0;
Ângulo de espalhamento da partícula 2: θ2.

Solução

Aplicando o Princípio da Conservação da Quantidade de Movimento (Figura 1)

\[ \begin{gather} {\mathbf{Q}}_{i}={\mathbf{Q}}_{f}\\ {\mathbf{Q}}_{1i}+{\mathbf{Q}}_{2i}={\mathbf{Q}}_{1f}+{\mathbf{Q}}_{2f}\\ m_{1}{\mathbf{v}}_{1i}+m_{2}{\mathbf{v}}_{2i}=m_{1}{\mathbf{v}}_{1f}+m_{2}{\mathbf{v}}_{2f} \end{gather} \]

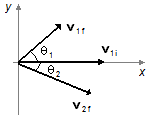
Figura 1

Sendo i e j os vetores unitários nas direções x e y, a velocidade inicial da partícula 1 só possui componente na direção i

\[ {\mathbf{v}}_{1i}=v_{1i}\;\mathbf{i} \]

as velocidades finais das partículas 1 e 2 podem ser decompostas nas direções i e j (Figura 1)

\[ {\mathbf{v}}_{1f}=v_{1f}\cos \theta_{1}\;\mathbf{i}+v_{1f}\operatorname{sen}\theta_{1}\;\mathbf{j} \]

\[ {\mathbf{v}}_{2f}=v_{2f}\cos \theta_{2}\;\mathbf{i}-v_{2f}\operatorname{sen}\theta_{2}\;\mathbf{j} \]

\[ \begin{gather} m_{1}v_{1i}\;\mathbf{i}+m_{2}.0=m_{1}(v_{1f}\cos\theta _{1}\;\mathbf{i}+v_{1f}\operatorname{sen}\theta_{1}\;\mathbf{j})+m_{2}(v_{2f}\cos \theta_{2}\;\mathbf{i}-v_{2f}\operatorname{sen}\theta_{2}\;\mathbf{j})\\ m_{1}v_{1i}\;\mathbf{i}=m_{1}v_{1f}\cos\theta _{1}\;\mathbf{i}+m_{1}v_{1f}\operatorname{sen}\theta_{1}\;\mathbf{j}+m_{2}v_{2f}\cos \theta_{2}\;\mathbf{i}-m_{2}v_{2f}\operatorname{sen}\theta_{2}\;\mathbf{j} \end{gather} \]

Separando as componentes temos um sistema de duas equações a duas incógnitas (v_1f e v_2f)

\[ \left\{ \begin{align} &\;m_{1}v_{1f}\cos \theta_{1}+m_{2}v_{2f}\cos\theta_{2}=m_{1}v_{1i}\\ &\;m_{1}v_{1f}\operatorname{sen}\theta_{1}-m_{2}v_{2f}\operatorname{sen}\theta_{2}=0 \end{align} \right. \]

Isolando o valor de v_2f na segunda equação e substituindo na primeira

\[ \begin{gather} m_{2}v_{2f}\operatorname{sen}\theta_{2}=m_{1}v_{1f}\operatorname{sen}\theta_{1}\\ v_{2f}=\frac{m_{1}v_{1f}\operatorname{sen}\theta_{1}}{m_{2}\operatorname{sen}\theta_{2}} \tag{I} \end{gather} \]

\[ \begin{gather} m_{1}v_{1f}\cos \theta_{1}+m_{2}\left(\frac{m_{1}v_{1f}\operatorname{sen}\theta_{1}}{m_{2}\operatorname{sen}\theta_{2}}\right)\cos \theta_{2}=m_{1}v_{1i}\\[5pt] m_{1}v_{1f}\cos \theta_{1}+\frac{m_{1}v_{1f}\operatorname{sen}\theta_{1}}{\operatorname{sen}\theta_{2}}\cos\theta_{2}=m_{1}v_{1i}\\[5pt] v_{1f}\cos \theta_{1}+\frac{v_{1f}\operatorname{sen}\theta_{1}}{\operatorname{sen}\theta_{2}}\cos\theta_{2}=v_{1i}\\[5pt] v_{1f}\left(\cos \theta_{1}+\frac{\cos \theta_{2}}{\operatorname{sen}\theta_{2}}\operatorname{sen}\theta_{1}\right)=v_{1i} \end{gather} \]

sendo \( \dfrac{\cos \theta_{2}}{\operatorname{sen}\theta_{2}}=\operatorname{cotg}\theta_{2} \)

\[ v_{1f}\left(\cos \theta_{1}+\text{cotg}\theta_{2}\operatorname{sen}\theta_{1}\right)=v_{1i} \]

\[ \bbox[#FFCCCC,10px] {v_{1f}=\frac{v_{1i}}{\cos \theta_{1}+\operatorname{cotg}\theta_{2}\operatorname{sen}\theta_{1}}} \]

substituindo este valor na expressão (I)

\[ \begin{gather} v_{2f}=\frac{m_{1}\operatorname{sen}\theta_{1}}{m_{2}\operatorname{sen}\theta_{2}}\left(\frac{v_{1i}}{\cos \theta_{1}+\operatorname{cotg}\theta_{2}\operatorname{sen}\theta_{1}}\right)\\[8pt] v_{2f}=\frac{m_{1}}{m_{2}}\left[\frac{v_{1i}\operatorname{sen}\theta_{1}}{\operatorname{sen}\theta_{2}\cos \theta_{1}+\operatorname{sen}\theta_{2}\left(\frac{\cos \theta_{2}}{\operatorname{sen}\theta_{2}}\right)\operatorname{sen}\theta_{1}}\right]\\[8pt] v_{2f}=\frac{m_{1}}{m_{2}}\left(\frac{v_{1i}\operatorname{sen}\theta_{1}}{\operatorname{sen}\theta_{2}\cos \theta_{1}+\cos \theta_{2}\operatorname{sen}\theta_{1}}\right) \end{gather} \]

lembrando que \( \operatorname{sen}(a+b)=\operatorname{sen}a\cos b+\operatorname{sen}b\cos a \),

\[ \operatorname{sen}(a+b)=\operatorname{sen}a\cos b+\operatorname{sen}b\cos a \]

\[ \bbox[#FFCCCC,10px] {v_{2f}=\frac{m_{1}}{m_{2}}\frac{v_{1i}\operatorname{sen}\theta_{1}}{\operatorname{sen}(\theta_{1}+\theta_{2})}} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .