Exercício Resolvido de Oscilações Harmônicas
publicidade
Um corpo, de massa m, está suspenso pela extremidade de uma mola, de constante elástica k, a outra
extremidade da mola está presa ao teto. Afasta-se o corpo da posição de equilíbrio e libera-se o corpo.
Desprezando a massa da mola e a resistência do ar com o sistema durante a oscilação, determine:
a) A equação de movimento do corpo;
b) A velocidade em função do tempo;
c) O módulo da velocidade máxima;
d) A aceleração em função do tempo;
e) O módulo da aceleração máxima;
f) A energia cinética;
g) A energia potencial;
h) A energia total.
a) A equação de movimento do corpo;
b) A velocidade em função do tempo;
c) O módulo da velocidade máxima;
d) A aceleração em função do tempo;
e) O módulo da aceleração máxima;
f) A energia cinética;
g) A energia potencial;
h) A energia total.
Dados do problema:
- Massa do corpo: m;
- Constante elástica da mola: k;
- Adotemos a aceleração da gravidade igual a g.
Inicialmente a mola está presa ao teto, como o problema nos diz para desprezar a massa da mola seu comprimento é o mesmo que ela possui quando em equilíbrio sobre um plano horizontal (a mola não se estica sob a ação do seu próprio peso), a extremidade livre da mola está numa posição de equilíbrio z0 (Figura 1-A). A massa m é presa à extremidade livre da mola, a mola se estica até atingir uma nova posição de equilíbrio O onde a força peso do corpo e a força elástica de restauração da mola se anulam (Figura 1-B). O corpo de massa m é puxado até uma posição z (Figura 1-C) e solto, a força elástica da mola atuará no sentido de restabelecer o equilíbrio.
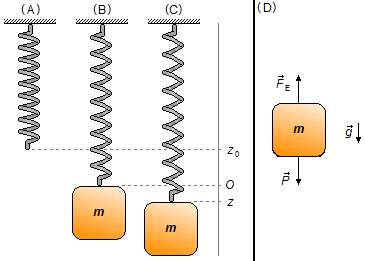
Adota-se um sistema de referência com sentido positivo para a baixo, no mesmo sentido da aceleração da gravidade (\( \vec{g} \)), no bloco atuam a força peso (\( \vec{P} \)) e a força elástica (\( {\vec{F}}_{E} \)), Figura 1-D.
Solução
a) Aplicando a 2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F=m\frac{d^{2}x}{dt^{2}}} \tag{I}
\end{gather}
\]
A força elástica da mola é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{E}=-kx} \tag{II-a}
\end{gather}
\]
e a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{II-b}
\end{gather}
\]
o sinal de negativo na força elástica representa que ela atua contra o sentido do deslocamento do bloco
(atua no sentido de restabelecer o equilíbrio). Substituindo as expressões (II-a) e (II-b) na expressão (I)
\[
\begin{gather}
-kx+mg=m\frac{d^{2}x}{dt^{2}}\\
m\frac{d^{2}x}{dt^{2}}+kx=mg
\end{gather}
\]
esta é uma Equação Diferencial Ordinária Não-Homogênea de 2.ª Ordem. Dividindo toda a equação pela
massa (m)
\[
\frac{d^{2}x}{dt^{2}}+\frac{k}{m}x=g
\]
fazendo a definição
\( \omega_{0}^{2}\equiv \frac{k}{m} \),
escrevemos
\[
\frac{d^{2}x}{dt^{2}}+\omega_{0}^{2}x=g
\]
Solução de \( \displaystyle \frac{d^{2}x}{dt^{2}}+\omega_{0}^{2}x=g \)
a solução desta equação será
a solução desta equação será
\[
\begin{gather}
x=x_{h}+x_{p} \tag{III}
\end{gather}
\]
onde xh é a solução da equação homogênea (igualando a zero), e xp é a solução
particular levando em consideração o termo do lado direito da igualdade (no caso a aceleração da gravidade
g).
- Solução homogênea
\[
\frac{d^{2}x_{h}}{dt^{2}}+\omega_{0}^{2}x_{h}=0
\]
A solução deste tipo de equação é encontrada igualando a zero e fazendo-se as substituições
\[
\begin{array}{l}
x_{h}=\operatorname{e}^{\lambda t}\\
\dfrac{dx_{h}}{dt}=\lambda \operatorname{e}^{\lambda t}\\
\dfrac{d^{2}x_{h}}{dt^{2}}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{array}
\]
\[
\begin{gather}
\lambda^{2}\operatorname{e}^{\lambda t}+\omega_{0}^{2}\operatorname{e}^{\lambda t}=0\\
\operatorname{e}^{\lambda t}\left(\lambda^{2}+\omega_{0}^{2}\right)=0\\
\lambda^{2}+\omega_{0}^{2}=\frac{0}{\operatorname{e}^{\lambda t}}\\
\lambda^{2}+\omega_{0}^{2}=0\\
\lambda^{2}=-\omega_{0}^{2}\\
\lambda =\sqrt{-\omega_{0}^{2}}\\
\lambda_{1,2}=\pm \omega_{0}\operatorname{i}
\end{gather}
\]
a solução será
\[
\begin{gather}
x_{h}=C_{1}\operatorname{e}^{\lambda_{1}t}+C_{2}\operatorname{e}^{\lambda_{2}t}\\
x_{h}=C_{1}\operatorname{e}^{\omega_{0}\operatorname{i}t}+C_{2}\operatorname{e}^{-\omega_{0}\operatorname{i}t}
\end{gather}
\]
onde C1 e C2 são constantes de integração, usando a Relação de Euler
(leia-se óiler)
\( \operatorname{e}^{\operatorname{i}\theta}=\cos \theta+\operatorname{i}\operatorname{sen}\theta \)
\[
\begin{gather}
x_{h}=C_{1}\left(\cos \omega_{0}t+\operatorname{i}\operatorname{sen}\omega_{0}t\right)+C_{2}\left(\cos m\omega_{0}t-\operatorname{i}\operatorname{sen}\omega_{0}t\right)\\
x_{h}=C_{1}\cos \omega_{0}t+\operatorname{i}C_{1}\operatorname{sen}\omega_{0}t+C_{2}\cos\omega_{0}t-\operatorname{i}C_{2}\operatorname{sen}\omega_{0}t
\end{gather}
\]
coletando os termos em seno e cosseno
\[
\begin{gather}
x_{h}=\left(C_{1}+C_{2}\right)\cos \omega_{0}t+\left(\operatorname{i}C_{1}-\operatorname{i}C_{2}\right)\operatorname{sen}\omega_{0}t\\
x_{h}=\left(C_{1}+C_{2}\right)\cos \omega_{0}t+\operatorname{i}\left(C_{1}-C_{2}\right)\operatorname{sen}\omega_{0}t
\end{gather}
\]
definindo duas novas constantes α e β em termos de C1 e C2
\[
\begin{array}{l}
\alpha \equiv C_{1}+C_{2}\\[8pt]
\beta \equiv\operatorname{i}(C_{1}-C_{2})
\end{array}
\]
\[
x_{h}=\alpha \cos \omega_{0}t+\beta \operatorname{sen}\omega_{0}t
\]
multiplicando e dividindo esta expressão por
\( \sqrt{\alpha ^{2}+\beta ^{2}\;} \)
\[
\begin{gather}
x_{h}=\left(\alpha \cos \omega_{0}t+\beta\operatorname{sen}\omega_{0}t\right)\frac{\sqrt{\alpha ^{2}+\beta^{2}\;}}{\sqrt{\alpha ^{2}+\beta^{2}\;}}\\
x_{h}=\sqrt{\alpha^{2}+\beta ^{2}\;}\left(\frac{\alpha }{\sqrt{\alpha^{2}+\beta^{2}\;}}\cos \omega_{0}t+\frac{\beta }{\sqrt{\alpha ^{2}+\beta^{2}\;}}\operatorname{sen}\omega_{0}t\right)
\end{gather}
\]
fazendo as seguintes definições
\[
\begin{array}{l}
A\equiv \sqrt{\alpha ^{2}+\beta ^{2}\;}\\
\cos\varphi \equiv \dfrac{\alpha }{\sqrt{\alpha ^{2}+\beta^{2}\;}}\\
\operatorname{sen}\varphi \equiv \dfrac{\beta }{\sqrt{\alpha^{2}+\beta^{2}\;}}
\end{array}
\]
\[
x_{h}=A(\cos \varphi \cos \omega_{0}t+\operatorname{sen}\varphi\operatorname{sen}\omega_{0}t)
\]
Observação: Lembrando da seguinte propriedade trigonométrica
\[
cos(a-b)=\cos a\cos b+\operatorname{sen}a\operatorname{sen}b
\]
\[
\begin{gather}
x_{h}=A\cos (\omega_{0}t-\varphi) \tag{IV}
\end{gather}
\]
- Solução particular
\[
\frac{d^{2}x_{p}}{dt^{2}}+\omega_{0}^{2}x_{p}=g
\]
A solução deste tipo de equação é encontrada tomando-se a equação igual à função do lado direito da igualdade. Como
neste caso o lado direito é uma função constante (a aceleração da gravidade g) a solução particular deve ser
uma constante C, fazendo as seguintes substituições
\[
\begin{array}{l}
x_{p}=C\\
\dfrac{dx_{p}}{dt}=0\\
\dfrac{d^{2}x_{p}}{dt^{2}}=0
\end{array}
\]
\[
\begin{gather}
0+\omega_{0}^{2}C=g\\
C=\frac{g}{\omega_{0}^{2}}
\end{gather}
\]
usando a definição de
\( \omega_{0}^{2} \)
feita acima
\[
C=\frac{mg}{k}
\]
assim a solução particular será
\[
\begin{gather}
x_{p}=\frac{mg}{k} \tag{V}
\end{gather}
\]
substituindo as expressões (IV) e (V) na expressão (III)
\[
x=A\cos (\omega_{0}t-\varphi)+\frac{mg}{k}
\]
\[ \bbox[#FFCCCC,10px]
{x=A\cos (\omega_{0}t-\varphi)+\frac{mg}{k}}
\]
Observação: O termo
\( \frac{mg}{k} \)
representa o deslocamento da posição de equilíbrio da mola, sem o corpo (z0 na Figura 1-A) e a nova
posição de equilíbrio, depois de colocada a massa m (O na Figura 1-B). A massa então oscila em torno da
nova posição de equilíbrio proporcional a uma função cosseno da mesma forma que um corpo na horizontal oscila em torno
da posição de equilíbrio da mola.
b) A velocidade é dada por
\[ \bbox[#99CCFF,10px]
{v=\frac{dx}{dt}}
\]
Derivada de \( x=A\cos (\omega_{0}t-\varphi)+\dfrac{mg}{k} \)
a função x(t) é uma função composta cuja derivada, pela regra da cadeia, é do tipo
a função x(t) é uma função composta cuja derivada, pela regra da cadeia, é do tipo
\[
\frac{dx[u(t)]}{dt}=\frac{dx}{du}\frac{du}{dt}
\]
com
\( x(u)=A\cos u \)
e
\( u(t)=\omega_{0}t-\varphi \),
assim as derivadas serão
\[
\begin{array}{l}
\dfrac{dx}{du}=-\operatorname{sen}u=-\operatorname{sen}(\omega_{0}t-\varphi )\\[8pt]
\dfrac{du}{dt}=\omega_{0}
\end{array}
\]
\[
\frac{dx}{dt}=A\left[-\operatorname{sen}(\omega_{0}t-\varphi).\omega_{0}\right]=-\omega_{0}A\operatorname{sen}(\omega_{0}t-\varphi)
\]
Como o termo
\( \frac{mg}{k} \)
é constante sua derivada é nula.
\[
v=-\omega_{0}A\operatorname{sen}(\omega_{0}t-\varphi)+0
\]
\[ \bbox[#FFCCCC,10px]
{v=-\omega_{0}A\operatorname{sen}(\omega_{0}t-\varphi)}
\]
c) Na solução do item (b) a velocidade terá um valor máximo quando \( \operatorname{sen}(\omega_{0}t-\varphi)=1 \), assim o módulo da velocidade máxima será
\[
\begin{gather}
\left|\;v_{max}\;\right|=\omega_{0}A\underbrace{\operatorname{sen}(\omega_{0}t-\varphi)}_{1}\\
\left|\;v_{max}\;\right|=\omega_{0}A
\end{gather}
\]
usando a definição de
\( \omega_{0}^{2} \)
feita acima
\[ \bbox[#FFCCCC,10px]
{\left|\;v_{max}\;\right|=A\sqrt{\frac{k}{m}\;}}
\]
d) A aceleração é dada por
\[ \bbox[#99CCFF,10px]
{a=\frac{dv}{dt}}
\]
derivando a solução do item (b)
Derivada de \( v=-\omega_{0}A\operatorname{sen}(\omega_{0}t-\varphi) \)
a função v(t) é uma função composta cuja derivada, pela regra da cadeia, é do tipo
a função v(t) é uma função composta cuja derivada, pela regra da cadeia, é do tipo
\[
\frac{dx[u(t)]}{dt}=\frac{dx}{du}\frac{du}{dt}
\]
com
\( v(u)=-\omega_{0}A\operatorname{sen}u \)
e
\( u(t)=\omega_{0}t-\varphi \),
assim as derivadas serão
\[
\begin{array}{l}
\dfrac{dv}{du}=-\omega_{0}A\cos u=-\omega_{0}A\cos(\omega_{0}t-\varphi)\\[8pt]
\dfrac{du}{dt}=\omega_{0}
\end{array}
\]
\[
\frac{dv}{dt}=-\omega_{0}A\left[\cos (\omega_{0}t-\varphi)\omega_{0}\right]=-\omega_{0}^{2}A\cos (\omega_{0}t-\varphi)
\]
\[ \bbox[#FFCCCC,10px]
{a=-\omega_{0}^{2}A\cos (\omega_{0}t-\varphi)}
\]
e) Na solução do item (d) a aceleração terá um valor máximo quando \( \cos (\omega_{0}t-\varphi)=1 \), assim o módulo da aceleração máxima será
\[
\begin{gather}
\left|\;a_{max}\;\right|=\omega_{0}^{2}A\underbrace{\cos (\omega_{0}t-\varphi)}_{1}\\
\left|\;a_{max}\;\right|=\omega_{0}^{2}A
\end{gather}
\]
usando a definição de
\( \omega_{0}^{2} \)
feita acima
\[ \bbox[#FFCCCC,10px]
{\left|\;a_{max}\;\right|=\frac{k}{m}A}
\]
f) A energia cinética é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_{C}=\frac{m v^{2}}{2}} \tag{VI}
\end{gather}
\]
substituindo a solução do item (b) na expressão (VI)
\[
\begin{gather}
E_{C}=\frac{m\left[-\omega_{0}A\operatorname{sen}(\omega_{0}t-\varphi)\right]^{2}}{2}\\
E_{C}=\frac{m\omega_{0}^{2}A^{2}\operatorname{sen}^{2}(\omega_{0}t-\varphi)}{2}
\end{gather}
\]
substituindo a definição de
\( \omega_{0}^{2} \)
feita acima
\[
E_{C}=m\frac{k}{m}\frac{A^{2}\operatorname{sen}^{2}(\omega_{0}t-\varphi)}{2}
\]
\[ \bbox[#FFCCCC,10px]
{E_{C}=\frac{kA^{2}}{2}\operatorname{sen}^{2}(\omega_{0}t-\varphi)}
\]
g) A energia potencial elástica é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E_{P}=\frac{kx^{2}}{2}} \tag{VII}
\end{gather}
\]
substituindo a solução do item (a) na expressão (VII)
\[
\begin{gather}
E_{P}=\frac{k\left[A\cos (\omega_{0}t-\varphi)+\frac{mg}{k}\right]^{2}}{2}\\
E_{P}=\frac{1}{2}k\left[A^{2}\cos^{2}(\omega_{0}t-\varphi)+2A\cos (\omega_{0}t-\varphi)\frac{mg}{k}+\frac{m^{2}g^{2}}{k^{2}}\right]\\
E_{P}=\frac{kA^{2}}{2}\cos^{2}(\omega_{0}t-\varphi)+A\cos (\omega_{0}t-\varphi)mg+\frac{m^{2}g^{2}}{2k}
\end{gather}
\]
podemos reescrever a solução do item (a) como
\( A\cos (\omega_{0}t-\varphi)=x-\dfrac{mg}{k} \)
\[
\begin{gather}
E_{P}=\frac{kA^{2}}{2}\cos ^{2}(\omega_{0}t-\varphi)+\left(x-\frac{mg}{k}\right)mg+\frac{m^{2}g^{2}}{2k}\\
E_{P}=\frac{kA^{2}}{2}\cos^{2}(\omega_{0}t-\varphi)+xmg-\frac{m^{2}g^{2}}{k}+\frac{m^{2}g^{2}}{2k}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{E_{P}=\frac{kA^{2}}{2}\cos ^{2}(\omega_{0}t-\varphi)+xmg-\frac{m^{2}g^{2}}{2k}}
\]
h) A energia total será dada pela soma dos resultados dos itens (f) e (g)
\[
\begin{gather}
E_{T}=E_{C}+E_{P}\\
E_{T}=\frac{kA^{2}}{2}\operatorname{sen}^{2}(\omega_{0}t-\varphi)+\frac{kA^{2}}{2}\cos ^{2}(\omega_{0}t-\varphi)+xmg-\frac{m^{2}g^{2}}{2k}\\
E_{T}=\frac{kA^{2}}{2}\left[\operatorname{sen}^{2}(\omega_{0}t-\varphi)+\cos ^{2}(\omega_{0}t-\varphi)\right]+xmg-\frac{m^{2}g^{2}}{2k}
\end{gather}
\]
da Trigonometria temos que
\( \cos ^{2}\theta +\operatorname{sen}^{2}\theta =1 \)
\[ \bbox[#FFCCCC,10px]
{E_{T}=\frac{kA^{2}}{2}+xmg-\frac{m^{2}g^{2}}{2k}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .