Exercício Resolvido de Oscilações Harmônicas
publicidade
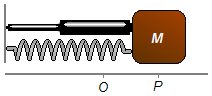
Um bloco de massa m = 0,25 kg é ligado a uma mola de constante elástica k = 16,25 N/m e a um
amortecedor de constante de amortecimento b = 0,5 N.s/m. O bloco é deslocado de sua posição de equilíbrio
O até um ponto P a 0,1 m e lançado se afastando do ponto de equilíbrio com velocidade inicial de
0,7 m/s. Adotando que a força de amortecimento é proporcional a velocidade, determine:
a) A equação do movimento;
b) Classifique o tipo de oscilação;
c) O gráfico da posição x em função do tempo t.
a) A equação do movimento;
b) Classifique o tipo de oscilação;
c) O gráfico da posição x em função do tempo t.
Dados do problema:
- Massa do corpo: m = 0,25 kg;
- Constante elástica da mola: k = 16,25 N/m;
- Constante de amortecimento: b = 0,5 N.s/m;
- Posição inicial (t = 0): x0 = 0,1 m;
- Velocidade inicial (t = 0): v0 = 0,7 m/s.
Adota-se um sistema de referência com sentido positivo para a direita. O bloco é deslocado até a posição
x0 = 0,1 m e lançado com velocidade inicial v0 = 0,7 m/s no mesmo sentido
do referencial. Quando solto a força elástica da mola atuará no sentido de restabelecer a posição de equilíbrio
(Figura 1). Com isto escrevemos as Condições Iniciais do problema:

Figura 1
a) Aplicando a 2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F=m\frac{d^{2}x}{dt^{2}}} \tag{I}
\end{gather}
\]
temos que as forças que atuam no bloco são a força elástica da mola
(\( {\vec{F}}_{E} \))
e a força de amortecimento
(\( {\vec{F}}_{R} \)),
dadas, em módulo, por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{E}=-kx} \tag{II-a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{R}=-bv=-b\frac{dx}{dt}} \tag{II-b}
\end{gather}
\]
o sinal de negativo na força elástica representa que ela atua contra o sentido do deslocamento do bloco
(atua no sentido de restabelecer o equilíbrio), na força de amortecimento representa que ela atua
contra o sentido da velocidade (atua no sentido de frear o movimento). Substituindo as expressões de (II)
em (I)
\[
\begin{gather}
-kx-b\frac{dx}{dt}=m\frac{d^{2}x}{dt^{2}}\\
m\frac{d^{2}x}{dt^{2}}+b\frac{dx}{dt}+kx=0
\end{gather}
\]
esta é uma Equação Diferencial Ordinária de 2.ª Ordem. Dividindo toda a equação pela massa (m)
\[
\frac{d^{2}x}{dt^{2}}+\frac{b}{m}\frac{dx}{dt}+\frac{k}{m}x=0
\]
substituindo os valores dados no problema
\[
\begin{gather}
\frac{d^{2}x}{dt^{2}}+\frac{0,5}{0,25}\frac{dx}{dt}+\frac{16,25}{0,25}x=0\\
\frac{d^{2}x}{dt^{2}}+2\frac{dx}{dt}+65x=0 \tag{III}
\end{gather}
\]
Solução de \( \displaystyle \frac{d^{2}x}{dt^{2}}+2\frac{dx}{dt}+65x=0 \)
a solução deste tipo de equação é encontrada fazendo-se as substituições
Derivada de \( x=A\operatorname{e}^{-t}\cos (8 t-\varphi ) \)
derivando o produto de funções na forma:
a solução deste tipo de equação é encontrada fazendo-se as substituições
\[
\begin{array}{l}
x=\operatorname{e}^{\lambda t}\\
\dfrac{dx}{dt}=\lambda \operatorname{e}^{\lambda t}\\
\dfrac{d^{2}x}{dt^{2}}=\lambda ^{2}\operatorname{e}^{\lambda t}
\end{array}
\]
\[
\begin{gather}
\lambda ^{2}\operatorname{e}^{\lambda t}+2\lambda\operatorname{e}^{\lambda t}+65\operatorname{e}^{\lambda t}=0\\
\operatorname{e}^{\lambda t}\left(\lambda ^{2}+2\lambda+65\right)=0\\
\lambda ^{2}+2\lambda+65=\frac{0}{{\operatorname{e}}^{\lambda t}}\\
\lambda ^{2}+2\lambda+65=0
\end{gather}
\]
esta é a Equação Característica que tem como solução
\[
\Delta =b^{2}-4ac=2^{2}-4.1.65=4-260=-256
\]
para Δ<0 as raízes são complexas da forma
\( a+b\text{i} \),
onde
\( \text{i}=\sqrt{-1} \)
\[
\begin{gather}
\lambda =\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-2\pm\sqrt{-256\;}}{2.1}=\frac{-2\pm 16\text{i}}{2}\\
\lambda_{1}=-1+8\text{i}\qquad\mathrm{e}\qquad \lambda_{2}=-1-8\text{i}
\end{gather}
\]
como Δ<0 a solução da expressão (III) é escrita como
\[
\begin{gather}
x=C_{1}\operatorname{e}^{\lambda_{1}t}+C_{2}\operatorname{e}^{\lambda_{2}t}\\
x=C_{1}\operatorname{e}^{(-1+8\text{i})t}+C_{2}\operatorname{e}^{(-1-8\text{i})t}
\end{gather}
\]
onde C1 e C2 são constantes de integração. Aplicando a propriedade
\( a^{m+n}=a^{m}.a^{n} \)
reescrevemos
\[
\begin{gather}
x=C_{1}\operatorname{e}^{-t}.\operatorname{e}^{8\text{i}t}+C_{2}\operatorname{e}^{-t}.\operatorname{e}^{-8\text{i}t}\\
x=\operatorname{e}^{-t}\left(C_{1}\operatorname{e}^{8\text{i}t}+C_{2}\operatorname{e}^{-8\text{i}t}\right)
\end{gather}
\]
usando a Relação de Euler (leia-se óiler)
\( \operatorname{e}^{i\theta }=\cos \theta+\text{i}\operatorname{sen}\theta \)
\[
\begin{gather}
x=\operatorname{e}^{-t}\left[C_{1}\left(\cos8t+\text{i}\operatorname{sen}8t\right)+C_{2}\left(\cos8t-\text{i}\operatorname{sen}8t\right)\right]\\
x=\operatorname{e}^{-t}\left[C_{1}\cos8t+\text{i}C_{1}\operatorname{sen}8t+C_{2}\cos8t-\text{i}C_{2}\operatorname{sen}8t\right]
\end{gather}
\]
coletando os termos em seno e cosseno
\[
\begin{gather}
x=\operatorname{e}^{-t}\left[\left(C_{1}+C_{2}\right)\cos8t+\left(\text{i}C_{1}-\text{i}C_{2}\right)\operatorname{sen}8t\right]\\
x=\operatorname{e}^{-t}\left[\left(C_{1}+C_{2}\right)\cos8t+\text{i}\left(C_{1}-C_{2}\right)\operatorname{sen}8t\right]
\end{gather}
\]
definindo duas novas constantes α e β em termos de C1 e C2
\[
\begin{gather}
\alpha \equiv C_{1}+C_{2}\\
\text{e}\\
\beta \equiv \text{i}(C_{1}-C_{2})
\end{gather}
\]
\[
\begin{gather}
x=\operatorname{e}^{-t}\left(\alpha \cos 8t+\beta\operatorname{sen}8t\right) \tag{IV}
\end{gather}
\]
multiplicando e dividindo esta expressão por
\( \sqrt{\alpha ^{2}+\beta ^{2}\;} \)
\[
\begin{gather}
x=\operatorname{e}^{-t}\left(\alpha \cos 8t+\beta\operatorname{sen}8t\right)\frac{\sqrt{\alpha ^{2}+\beta^{2}\;}}{\sqrt{\alpha ^{2}+\beta ^{2}}}\\
x=\sqrt{\alpha ^{2}+\beta^{2}}\operatorname{e}^{-t}\left(\frac{\alpha }{\sqrt{\alpha ^{2}+\beta^{2}}}\cos 8t+\frac{\beta }{\sqrt{\alpha ^{2}+\beta^{2}\;}}\operatorname{sen}8t\right)
\end{gather}
\]
fazendo as seguintes definições
\[
\begin{gather}
A\equiv \sqrt{\alpha ^{2}+\beta ^{2}\;}\\
\cos \varphi\equiv \frac{\alpha }{\sqrt{\alpha ^{2}+\beta^{2}\;}}\\
\operatorname{sen}\varphi \equiv \frac{\beta }{\sqrt{\alpha^{2}+\beta ^{2}\;}}
\end{gather}
\]
\[
x=A\operatorname{e}^{-t}\left(\cos \varphi \cos8t+\operatorname{sen}\varphi \operatorname{sen}8t\right)
\]
Observação: Lembrando da Trigonometria
\[
(a-b)=\cos a\;\cos b+\operatorname{sen}a\;\operatorname{sen}b
\]
\[
\begin{gather}
x=A\operatorname{e}^{-t}\cos (8t-\varphi ) \tag{V}
\end{gather}
\]
onde A e φ são constantes de integração determinadas pelas Condições Iniciais, derivando a
expressão (V) em relação ao tempo
Derivada de \( x=A\operatorname{e}^{-t}\cos (8 t-\varphi ) \)
derivando o produto de funções na forma:
\[
(uv)'=u'v+uv'
\]
onde
\( u=A\operatorname{e}^{-t} \)
e
\( v=\cos (8t-\varphi ) \)
\[
\frac{du}{dt}=A(-1)e^{-t}=-A\operatorname{e}^{-t}
\]
e a função cosseno é uma função composta cuja derivada é do tipo
\[
\frac{dv[w(t)]}{dt}=\frac{dv}{dw}\frac{dw}{dt}
\]
com \( w=8t-\varphi \)
\[
\begin{array}{l}
\dfrac{dv}{dw}=-\operatorname{sen}w=-\operatorname{sen}(8t-\varphi)\\
\dfrac{dw}{dt}=8
\end{array}
\]
\[
\frac{dv}{dt}=-8\operatorname{sen}(8t-\varphi )
\]
\[
\begin{gather}
\frac{dx}{dt}=\left[\left(-A\operatorname{e}^{-t}\right)\cos(8t-\varphi)\right]+\left[A\operatorname{e}^{-t}\left(-8\operatorname{sen}(8t-\varphi)\right)\right]\\
\frac{dx}{dt}=-A\operatorname{e}^{-t}\cos (8t-\varphi)-8A\operatorname{e}^{-t}\operatorname{sen}(8t-\varphi)\\
\frac{dx}{dt}=-A\operatorname{e}^{-t}\left[\cos (8t-\varphi)+8\operatorname{sen}(8t-\varphi )\right] \tag{VI}
\end{gather}
\]
substituindo as Condições Iniciais nas expressões (V) e (VI)
\[
\begin{gather}
x(0)=0,1=A\operatorname{e}^{-0}\cos (8.0-\varphi)\\
0,1=A\operatorname{e}^{-0}\cos (8.0-\varphi )\\
0,1=A\cos (-\varphi)
\end{gather}
\]
como o cosseno é uma função par temos
\( \cos \varphi =\cos (-\varphi ) \)
\[
\begin{gather}
0,1=A\cos \varphi \tag{VII}
\end{gather}
\]
\[
\begin{gather}
\frac{dx(0)}{dt}=0,7=-A\operatorname{e}^{-0}\cos(8.0-\varphi )-8A\operatorname{e}^{-0}\operatorname{sen}(8.0-\varphi)\\
0,7=-A\operatorname{e}^{-0}\cos (8.0-\varphi)-8A\operatorname{e}^{-0}\operatorname{sen}(8.0-\varphi )\\
0,7=-A\cos(-\varphi )-8A\operatorname{sen}(-\varphi )
\end{gather}
\]
como o cosseno é uma função par e seno é uma função ímpar
\( \operatorname{sen}\varphi =-\operatorname{sen}(-\varphi ) \)
ficamos com
\[
\begin{gather}
0,7=-A\cos \varphi +8A\operatorname{sen}\varphi \tag{VIII}
\end{gather}
\]
isolando o valor de A na expressão (VII)
\[
\begin{gather}
A=\frac{0,1}{\cos \varphi } \tag{IX}
\end{gather}
\]
e substituindo na expressão (VIII)
\[
\begin{gather}
0,7=\frac{-{0,1}}{\cos \varphi }.\cos \varphi+8.\frac{0,1}{\cos \varphi }.\operatorname{sen}\varphi\\
0,7=-0,1+0,8\operatorname{tg}\varphi \\
0,8\operatorname{tg}\varphi=0,7+0,1\\
0,8\operatorname{tg}\varphi =0,8\\
\operatorname{tg}\varphi=\frac{0,8}{0,8}\\
\operatorname{tg}\varphi =1\\
\varphi=\operatorname{arctg}(1)\\
\varphi =\frac{\pi}{4}
\end{gather}
\]
substituindo o valor de φ na expressão (IX)
\[
\begin{gather}
A=\frac{0,1}{\cos \frac{\pi}{4}}\\
A=\frac{0,1}{\frac{\sqrt{2\;}}{2}}\\
A=\frac{0,1.2}{\sqrt{2\;}}\\
A=\frac{0,2}{\sqrt{2\;}}
\end{gather}
\]
multiplicando o numerador e o denominador por
\( \sqrt{2\;} \)
\[
\begin{gather}
A=\frac{0,2}{\sqrt{2\;}}.\frac{\sqrt{2\;}}{\sqrt{2\;}}\\
A=\frac{0,2\sqrt{2\;}}{2}\\A=0,1\sqrt{2\;}
\end{gather}
\]
substituindo as constantes A e φ na expressão (V)
\[
x(t)=0,1\sqrt{2\;}\operatorname{e}^{-t}\cos \left(8t-\frac{\pi}{4}\right)
\]
\[ \bbox[#FFCCCC,10px]
{x(t)=0,1\sqrt{2\;}\operatorname{e}^{-t}\cos \left(8t-\frac{\pi}{4}\right)}
\]
b) Como Δ<0 este é um oscilador subcrítico.
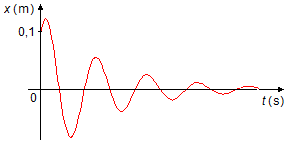
c) Construção do gráfico de
\[
\begin{gather}
x(t)=0,1\sqrt{2\;}\operatorname{e}^{-t}\cos \left(8t-\frac{\pi}{4}\right) \tag{X}
\end{gather}
\]
A função x(t) é o produto de duas funções,
\( f(t)=0,1\sqrt{2\;}\operatorname{e}^{-t} \)
e
\( g(t)=\cos \left(8t-\frac{\pi}{4}\right) \).
Para determinar as raízes fazemos x(t) = 0, como
x(t) = f(t)g(t) temos f(t) = 0 ou g(t) = 0.
- Para g(t) = 0
\[
\begin{gather}
g(t)=\cos \left(8t-\frac{\pi}{4}\right)=0\\
\cos\left(8t-\frac{\pi}{4}\right)=0
\end{gather}
\]
a função cosseno é zero quando seu argumento
\( \left(8t-\frac{\pi}{4}\right) \)
é igual a
\( \frac{\pi}{2} \),
\( \frac{3\pi}{2} \),
\( \frac{5\pi}{2} \),...,
\( \frac{(2n+1)\pi}{2} \),
com n = 0, 1, 2, 3,..., portanto devemos ter
\[
\begin{gather}
8t-\frac{\pi}{4}=\frac{(2n+1)\pi }{2}\\
8t=\frac{2\pi n}{2}+\frac{\pi}{2}+\frac{\pi}{4}\\
8t=\frac{4\pi n+2\pi +\pi}{4}\\
8t=\frac{4\pi n+3\pi }{4}\\
8t=\frac{(4n+3)\pi}{4}\\t=\frac{(4n+3)\pi }{4.8}\\
t=\frac{(4n+3)\pi}{32}
\end{gather}
\]
para esses valores de t temos as raízes da função cosseno, os quatro primeiros valores serão, para
n = 0, 1, 2 e 3, respectivamente, t = 0,29; 0,69; 1,08 e 1,47 (Gráfico 1).

- Para f(t) = 0
\[
\begin{gather}
f(t)=0,1\sqrt{2\;}\operatorname{e}^{-t}=0\\0,1\sqrt{2\;}\operatorname{e}^{-t}=0\\
\operatorname{e}^{-t}=\frac{0}{0,1\sqrt{2\;}}\\
\operatorname{e}^{-t}=0
\end{gather}
\]
como não exite t que satisfaça essa igualdade a função f(t) não cruza o eixo das abscissas.Para qualquer valor de t real a função será sempre positiva, f(t) > 0.
Derivando a expressão f(t)
\[
\begin{gather}
\frac{df}{dt}=(-1).0,1\sqrt{2\;}\operatorname{e}^{-t}\\
\frac{df}{dt}=-0,1\sqrt{2\;}\operatorname{e}^{-t}
\end{gather}
\]
para qualquer valor de t real a derivada será sempre negativa
\( \left(\frac{df(t)}{dt}<0\right) \)
e a função decresce sempre. Fazendo
\( \frac{df(t)}{dt}=0 \)
encontramos pontos de máximos e mínimos da função.
\[
\begin{gather}
\frac{df}{dt}=-0,1\sqrt{2\;}\operatorname{e}^{-t}=0\\
\operatorname{e}^{-t}=\frac{0}{-0,1\sqrt{2\;}}\\
\operatorname{e}^{-t}=0
\end{gather}
\]
como não exite t que satisfaça essa igualdade não existem pontos de máximo ou mínimo da função.Derivando uma segunda vez a função
\[
\begin{gather}
\frac{d^{2}f}{dt^{2}}=-(-1).0,1\sqrt{2\;}\operatorname{e}^{-t}\\
\frac{d^{2}f}{dt^{2}}=0,1\sqrt{2\;}\operatorname{e}^{-t}
\end{gather}
\]
para qualquer valor de t real a derivada segunda será sempre positiva
\( \left(\frac{d^{2}f(t)}{dt^{2}}>0\right) \)
e a função possui “boca” voltada para cima. Fazendo
\( \frac{d^{2}f(t)}{dt^{2}}=0 \)
encontramos pontos de inflexão na função.
\[
\begin{gather}
\frac{d^{2}f}{dt^{2}}=0,1\sqrt{2\;}\operatorname{e}^{-t}=0\\
0,1\sqrt{2\;}\operatorname{e}^{-t}=0\\
\operatorname{e}^{-t}=\frac{0}{0,1\sqrt{2\;}}\\
\operatorname{e}^{-t}=0
\end{gather}
\]
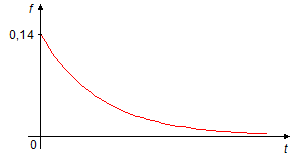
como não exite t que satisfaça essa igualdade não existem pontos de inflexão na função.Para t = 0 a expressão de f(0) fornece
\[
\begin{gather}
f(0)=0,1\sqrt{2\;}\operatorname{e}^{-0}\\
f(0)=0,1\sqrt{2\;}\\
f(0)=0,1.1,4\\
f(0)=0,14
\end{gather}
\]
Como a variável t representa o tempo não tem sentido o cálculo de valores negativos (t<0),
para t tendendo a infinito
\[
\lim _{t\rightarrow \infty }f(t)=\lim _{t\rightarrow \infty}0,1\sqrt{2\;}\operatorname{e}^{-t}=\lim _{t\rightarrow \infty}{\frac{0,1\sqrt{2\;}}{\operatorname{e}^{t}}}=0
\]
Da análise feita acima traçamos o gráfico de f em função de t (Gráfico 2).
Como x(t) = f(t)g(t) a combinação dos gráficos produz uma curva que
oscila como a função cosseno amortecida pela exponencial (Gráfico 3).
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .