Exercício Resolvido de Oscilações Harmônicas
publicidade
Um bloco de massa m = 2,50 kg é ligado a uma mola de constante elástica k = 12,00 N/m e
a um amortecedor de coeficiente de amortecimento b = 0,60 N.s/m. O bloco é deslocado de sua
posição de equilíbrio O até um ponto x0 a 0,20 m e liberado a partir do repouso.
Determine:
a) A equação do movimento;
b) Classifique o tipo de oscilação;
c) O gráfico da posição x em função do tempo t.
a) A equação do movimento;
b) Classifique o tipo de oscilação;
c) O gráfico da posição x em função do tempo t.
Dados do problema:
- Massa do corpo: m = 2,50 kg;
- Constante elástica da mola: k = 12,00 N/m;
- Coeficiente de amortecimento: b = 0,60 N.s/m;
- Posição inicial (t = 0): x0 = 0,20 m;
- Velocidade inicial (t = 0): v0 = 0.
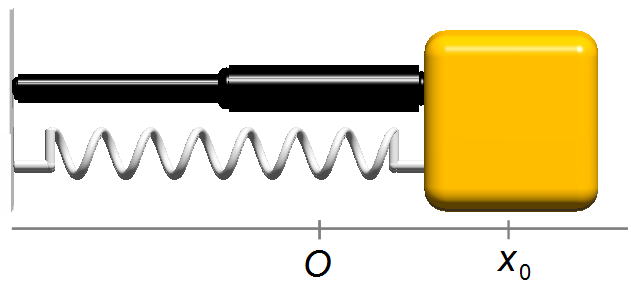
Adotamos um sistema de referência com sentido positivo para a direita. O bloco é deslocado até a posição
x0 = 0,20 m e liberadoo a partir do repouso, v0 = 0. Quando solto a
força elástica da mola atuará no sentido de restabelecer o posição de equilíbrio (Figura 1). Com isto
escrevemos as Condições Iniciais do problema
\[
\begin{gather}
x(0)=0,20\;\text{m}\\[10pt]
v_{0}=\frac{dx}{dt}=0
\end{gather}
\]
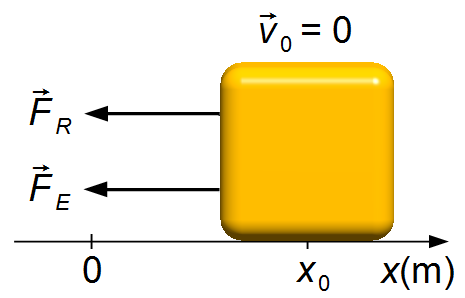
Solução
a) Aplicando a 2.ª Lei de Newton (Figura 1)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F=m\frac{d^{2}x}{dt^{2}}} \tag{I}
\end{gather}
\]
as forças que atuam no bloco são a força elástica da mola
\( {\vec{F}}_{E} \)
e a força de amortecimento
\( {\vec{F}}_{R} \)
dadas, em módulo, por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{E}=-kx} \tag{II-a}
\end{gather}
\]
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{R}=-bv=-b\frac{dx}{dt}} \tag{II-b}
\end{gather}
\]
o sinal de negativo na força elástica indica que ela atua contra o sentido do deslocamento do bloco
(atua no sentido de restabelecer o equilíbrio), na força de amortecimento indica que ela atua
contra o sentido da velocidade (atua no sentido de frear o movimento). Substituindo as expressões de
(II) na expressão (I)
\[
\begin{gather}
-kx-b\frac{dx}{dt}=m\frac{d^{2}x}{dt^{2}}\\[5pt]
m\frac{d^{2}x}{dt^{2}}+b\frac{dx}{dt}+kx=0
\end{gather}
\]
esta é uma Equação Diferencial Ordinária Homogênea de 2.ª Ordem. Dividindo toda a equação pela
massa m
\[
\begin{gather}
\frac{d^{2}x}{dt^{2}}+\frac{b}{m}\frac{dx}{dt}+\frac{k}{m}x=0
\end{gather}
\]
substituindo os valores dados no problema
\[
\begin{gather}
\frac{d^{2}x}{dt^{2}}+\frac{0,60}{2,50}\frac{dx}{dt}+\frac{12,00}{2,50}x=0\\[5pt]
\frac{d^{2}x}{dt^{2}}+0,24\frac{dx}{dt}+4,80x=0 \tag{III}
\end{gather}
\]
Solução de \( \frac{d^{2}x}{dt^{2}}+0,24\frac{dx}{dt}+4,80x=0 \)
A solução deste tipo de equação é encontrada fazendo-se as substituições
A solução deste tipo de equação é encontrada fazendo-se as substituições
\[
\begin{gather}
x=\operatorname{e}^{\lambda t}\\[5pt]
\frac{dx}{dt}=\lambda \operatorname{e}^{\lambda t}\\[5pt]
\frac{d^{2}x}{dt^{2}}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{gather}
\]
substituindo estes valores na equação diferencial
\[
\begin{gather}
\lambda^{2}\operatorname{e}^{\lambda t}+0,24\lambda\operatorname{e}^{\lambda t}+4,80\operatorname{e}^{\lambda t}=0\\[5pt]
\operatorname{e}^{\lambda t}\left(\lambda ^{2}+0,24\lambda+4,80\right)=0\\[5pt]
\lambda^{2}+0,24\lambda+4,80=\frac{0}{{\operatorname{e}}^{\lambda t}}\\[5pt]
\lambda^{2}+0,24\lambda +4,80=0
\end{gather}
\]
esta é a Equação Característica que tem como solução
\[
\begin{gather}
\Delta=b^{2}-4ac=0,24^{2}-4.1.4,80=0,06-19,20=-19,14
\end{gather}
\]
para Δ<0 as raízes são complexas da forma a+bi, onde
\( i=\sqrt{-1} \)
\[
\begin{gather}
\lambda=\frac{-b\pm \sqrt{\Delta\;}}{2a}=\frac{-0,24\pm \sqrt{-19,14\;}}{2.1}=\frac{-0,24\pm4,37i}{2}\\[5pt]
\lambda _{1}=-0,12+2,19i\qquad \text{e}\qquad \lambda_{2}=-0,12-2,19i
\end{gather}
\]
a solução da equação diferencial será
\[
\begin{gather}
x=C_{1}\operatorname{e}^{\lambda_{1}t}+C_{2}\operatorname{e}^{\lambda_{2}t}\\[5pt]
x=C_{1}\operatorname{e}^{(-0,12+2,19i)t}+C_{2}\operatorname{e}^{(-0,12-2,19i)t}\\[5pt]
x=C_{1}\operatorname{e}^{(-0,12t+2,19it)}+C_{2}\operatorname{e}^{(-0,12t-2,19it)}\\[5pt]
x=C_{1}\operatorname{e}^{-0,12t}\operatorname{e}^{2,19it}+C_{2}\operatorname{e}^{-0,12t}\operatorname{e}^{-2,19it}\\[5pt]
x=\operatorname{e}^{-0,12t}\left(C_{1}\operatorname{e}^{2,19it}+C_{2}\operatorname{e}^{-2,19it}\right)
\end{gather}
\]
onde C1 e C2 são constantes de integração, usando a
Fórmula de Euler
\( \operatorname{e}^{i\theta }=\cos \theta +i\operatorname{sen}\theta \)
\[
\begin{gather}
x=\operatorname{e}^{-0,12t}\left[C_{1}\left(\cos2,19t+\operatorname{i}\operatorname{sen}2,19t\right)+C_{2}\left(\cos2,19t-i\operatorname{sen}2,19 t\right)\right]\\[5pt]
x=\operatorname{e}^{-0,12t}\left[C_{1}\cos2,19t+iC_{1}\operatorname{sen}2,19t+C_{2}\cos2,19t-iC_{2}\operatorname{sen}2,19t\right]\\[5pt]
x=\operatorname{e}^{-0,12t}\left[\left(C_{1}+C_{2}\right)\cos2,19t+i\left(C_{1}-C_{2}\right)\operatorname{sen}2,19t\right]
\end{gather}
\]
definindo duas novas constantes α e β em termos de C1 e
C2
\[
\begin{gather}
\alpha \equiv C_{1}+C_{2}\\[5pt]
\text{e}\\[5pt]
\beta \equiv i(C_{1}-C_{2})
\end{gather}
\]
\[
\begin{gather}
x=\operatorname{e}^{-0,12t}\left(\alpha \cos 2,19t+\beta\operatorname{sen}2,19t\right) \tag{IV}
\end{gather}
\]
Derivada a expressão (IV) em relação ao tempo
\[
\begin{gather}
x=\underbrace{\operatorname{e}^{-0,12t}}_{u}\underbrace{\left(\alpha\cos2,19t+\beta \operatorname{sen}2,19t\right)}_{v}
\end{gather}
\]
usando a Regra do Produto para derivada de funções
\[
\begin{gather}
(uv)'=u'v+uv'
\end{gather}
\]
onde
\( u=\operatorname{e}^{-0,12t} \)
e
\( v=\left(\alpha \cos 2,19t+\beta \operatorname{sen}2,19t\right) \),
o termo entre parênteses é a derivada da soma dada pela soma das derivadas
\[
\begin{gather}
(f+g)'=f'+g'
\end{gather}
\]
e as funções seno e cosseno entre parênteses são funções compostas usando a Regra da Cadeia para
derivadas
\[
\begin{gather}
\frac{df[w(t)]}{dt}=\frac{df}{dw}\frac{dw}{dt}
\end{gather}
\]
com
\( f=\alpha \cos w \),
\( g=\beta \operatorname{sen}w \)
e
\( w=2,19t \)
\[
\begin{gather}
\frac{dx}{dt} =\frac{du}{dt}v+u\frac{dv}{dt}\\[5pt]
\frac{dx}{dt} =\frac{du}{dt}v+u\left(\frac{df}{dt}+\frac{dg}{dt}\right)\\[5pt]
\frac{dx}{dt} =\frac{du}{dt}v+u\left(\frac{df}{dw}\frac{dw}{dt}+\frac{dg}{dw}\frac{dw}{dt}\right)\\[5pt]
\frac{dx}{dt} =\frac{d\left(\operatorname{e}^{-0,12t}\right)}{dt}\left(\alpha\cos 2,19t+\beta\operatorname{sen}2,19t\right)+\\
+\left(\operatorname{e}^{-0,12t}\right)\left[\frac{d(\alpha\cos w)}{dw}\frac{d(2,19t)}{dt}+\frac{d(\beta\operatorname{sen}w)}{dw}\frac{d(2,19t)}{dt}\right]\\[5pt]
\frac{dx}{dt} =-0,12\operatorname{e}^{-0,12t}\left(\alpha\cos 2,19t+\beta\operatorname{sen}2,19t\right)+\\
+\left(\operatorname{e}^{-0,12t}\right)\left[(-\alpha\operatorname{sen}2,19t)(2,19)+(\beta \cos 2,19t)(2,19)\right]\\[5pt]
\frac{dx}{dt} =\operatorname{e}^{-0,12t}\left[\left(-0,12\alpha\cos 2,19t-0,12\beta\operatorname{sen}2,19t\right)\right.+\\
+\left.\left(-2,19\alpha\operatorname{sen}2,19t+2,19\beta \cos2,19t\right)\right]\\[5pt]
\frac{dx}{dt} =\operatorname{e}^{-0,12t}\left[\left(-0,12\alpha\cos 2,19t-2,19\alpha\operatorname{sen}2,19t\right)\right.+\\
+\left.\left(-0,12\beta\operatorname{sen}2,19t+2,19\beta \cos2,19t\right)\right]\\[5pt]
\frac{dx}{dt} =\operatorname{e}^{-0,12t}\left[-\alpha\left(0,12\cos 2,19t+2,19\operatorname{sen}2,19t\right)\right.+\\
+\left.\beta\left(2,19\cos2,19t-0,12\operatorname{sen}2,19t\right)\right] \tag{V}
\end{gather}
\]
Substituindo as Condições Iniciais nas expressões (IV) e (V)
\[
\begin{gather}
x(0)=0,20=\operatorname{e}^{-0,12.0}\left(\alpha \cos 2,19.0+\beta \operatorname{sen}2,19.0\right)\\[5pt]
\alpha=0,20 \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{dx(0)}{dt}=0=\operatorname{e}^{-0,12.0}\left[-0.20.\left(0,12\cos2,19.0+2,19\operatorname{sen}2,19.0\right)\right.\text{+}\\
\text{+}\left.\beta\left(2,19\cos2,19.0-0,12\operatorname{sen}2,19.0\right)\right]\qquad\\[5pt]
0=-0,20.\left(0,12.1+0\right)+\beta\left(2,19.1-0\right)\\[5pt]
0,02=\beta 2,19\\[5pt]\beta=\frac{0,02}{2,19}\\[5pt]
\beta =0,01 \tag{VII}
\end{gather}
\]
substituindo as constantes (VI) e (VI) na expressão (IV)
\[
\begin{gather}
x=\operatorname{e}^{-0,12t}\left(0,20\cos2,19t+0,01\operatorname{sen}2,19t\right)
\end{gather}
\]
Equação de movimento
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{x(t)=\operatorname{e}^{-0,12t}\left(0,20\cos2,19t+0,01\operatorname{sen}2,19t\right)}
\end{gather}
\]
b) Como Δ<0 este é um oscilador subcrítico.
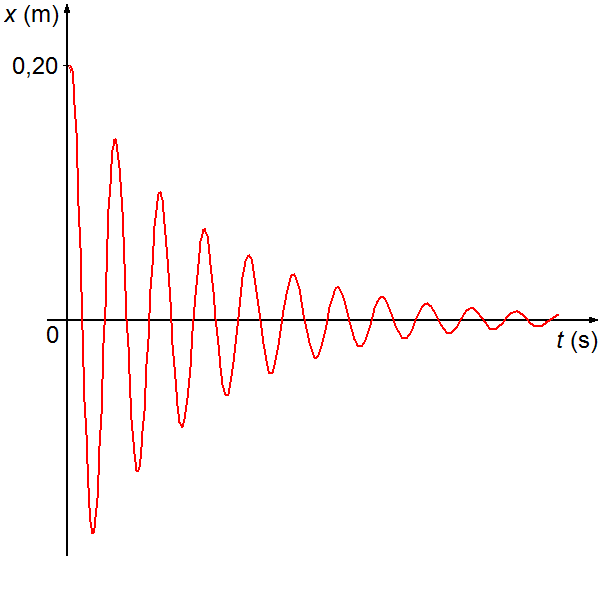
c) Construção do gráfico de
\[
\begin{gather}
x(t)=\operatorname{e}^{-0,12t}\left(0,20\cos2,19t+0,01\operatorname{sen}2,19t\right)
\end{gather}
\]
A função x(t) é o produto de duas funções,
\( f(t)=\operatorname{e}^{-0,12t} \)
e
\( g(t)=0,20\cos 2,19t+0,01\operatorname{sen}2,19t \).
Para determinar as raízes fazemos x(t) = 0, como
x(t) = f(t)g(t) temos f(t) = 0 ou
g(t) = 0.
- Para g(t) = 0
\[
\begin{gather}
g(t)=0,20\cos2,19t+0,01\operatorname{sen}2,19t=0\\[5pt]
0,01\operatorname{sen}2,19t=-0,20\cos2,19t\\[5pt]
\frac{\operatorname{sen}2,19t}{\cos2,19t}=-{\frac{0,20}{0,01}}\\[5pt]
\operatorname{tg}2,19t=-20\\[5pt]
2,19t=\operatorname{arctg}(-20)\\[5pt]
t=\frac{1}{2,19}\left[-\operatorname{arctg}(20)+n\pi\right]\\[5pt]
t=\frac{1}{2,19}\left[-1,52+n\pi \right]
\end{gather}
\]
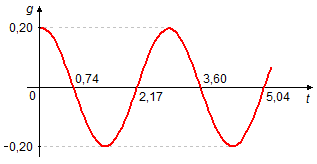
com n = 1, 2, 3,..., para esses valores de t temos as raízes da função g(t), os
quatro primeiros valores serão, para n = 1, 2, 3 e 4, respectivamente, t = 0,74; 2,17; 3,60
e 5,04 (Gráfico 1).
- Para f(t) = 0
\[
\begin{gather}
f(t)=\operatorname{e}^{-0,12t}=0\\[5pt]
\operatorname{e}^{-t}=0
\end{gather}
\]
como não exite t que satisfaça essa igualdade a função f(t) não cruza o eixo das
abscissas.Para qualquer valor de t real a função será sempre positiva, f(t) > 0.
Derivando a função f(t)
\[
\begin{gather}
\frac{df}{dt}=-0,12\operatorname{e}^{-0,12t}
\end{gather}
\]
para qualquer valor de t real a derivada será sempre negativa
\( \left(\frac{df(t)}{dt}<0\right) \)
e a função decresce sempre. Fazendo
\( \frac{df(t)}{dt}=0 \)
encontramos pontos de máximos e mínimos da função.
\[
\begin{gather}
\frac{df}{dt}=-0,12\operatorname{e}^{-0,12t}=0\\[5pt]
\operatorname{e}^{-0,12t}=\frac{0}{-0,12}\\[5pt]
\operatorname{e}^{-0,12t}=0
\end{gather}
\]
como não exite t que satisfaça essa igualdade não existem pontos de máximo ou mínimo da função.Derivando uma segunda vez a função f(t)
\[
\begin{gather}
\frac{d^{2}f}{dt^{2}}=-0,12(-0,12)\operatorname{e}^{-0,12t}\\[5pt]
\frac{d^{2}f}{dt^{2}}=0,01\operatorname{e}^{-0,12t}
\end{gather}
\]
para qualquer valor de t real a derivada segunda será sempre positiva
\( \left(\frac{d^{2}f(t)}{dt^{2}}>0\right) \)
e a função possui “boca” voltada para cima. Fazendo
\( \frac{d^{2}f(t)}{dt^{2}}=0 \)
encontramos pontos de inflexão na função.
\[
\begin{gather}
\frac{d^{2}f}{dt^{2}}=0,01\operatorname{e}^{-0,12t}=0\\[5pt]
\operatorname{e}^{-0,12t}=\frac{0}{0,01}\\[5pt]
\operatorname{e}^{-0,12t}=0
\end{gather}
\]
como não exite t que satisfaça essa igualdade não existem pontos de inflexão na função.Para t = 0 a expressão de f(0)
\[
\begin{gather}
f(0)=\operatorname{e}^{-0,12.0}\\[5pt]
f(0)=\operatorname{e}^{-0}\\[5pt]
f(0)=1
\end{gather}
\]
Como a variável t representa o tempo não tem sentido o cálculo de valores negativos,
t<0, para t tendendo a infinito
\[
\begin{gather}
\lim_{t\rightarrow \infty }f(t)=\lim_{t\rightarrow \infty}\operatorname{e}^{-0,12t}=\lim_{t\rightarrow \infty}{\frac{1}{\operatorname{e}^{0,12t}}}=0
\end{gather}
\]
Da análise feita acima traçamos o gráfico de f em função de t (Gráfico 2).
Como x(t) = f(t)g(t) a combinação dos gráficos produz uma curva que oscila como a função g(t) amortecida pela exponencial f(t) (Gráfico 3).
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .