Exercício Resolvido de Ondas
Português
English
publicidade
Duas ondas progressivas de mesma amplitude e mesma frequência possuem uma diferença de fase igual a φ. Determine a expressão da onda resultante da superposição destas duas ondas.
Dados do problema:
- Amplitude das ondas: y1 = y2 = a;
- Frequência angular das ondas: ω1 = ω2 = ω;
- Diferença de fase entre as duas ondas: φ.
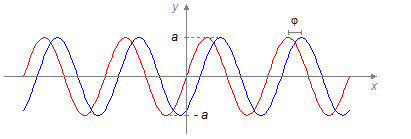
Consideramos duas ondas senoidais, onde uma delas (em vermelho) possui fase inicial nula e a outra (em azul) possui uma diferença de fase igual a φ em relação à primeira onda e ambas com amplitude a (Figura 1)
Solução
A função de onda é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{y(x,t)=A\cos (kx-\omega t)}
\end{gather}
\]
Escrevendo as funções de onda para as duas ondas
\[
\begin{gather}
y_{1}(x,t)=a\cos (kx-\omega t) \\[5pt]
\text{e}\\[5pt]
y_{2}(x,t)=a\cos (kx-\omega t+\varphi )
\end{gather}
\]
somando as duas ondas
\[
\begin{gather}
y(x,t)=a\cos (kx-\omega t)+a\cos (kx-\omega t+\varphi)\\[5pt]
y(x,t)=a[\cos (kx-\omega t)+\cos (kx-\omega t+\varphi)] \tag{I}
\end{gather}
\]
Observação: Lembrando de uma das Fórmulas de Prostaférese
\[
\begin{gather}
\cos a+\cos b=2\operatorname{sen}\left(\frac{a+b}{2}\right)\cos\left(\frac{a-b}{2}\right)
\end{gather}
\]
Fazendo as seguintes associações \( a=kx-\omega t \) e \( b=kx-\omega t+\varphi \), então a expressão (I) pode ser reescrita
\[
\begin{gather}
y(x,t)=a\left[2\operatorname{sen}\left(\frac{kx-\omega t+kx-\omega t+\varphi }{2}\right)\cos \left(\frac{kx-\omega t-(kx-\omega t+\varphi)}{2}\right)\right]\\[5pt]
y(x,t)=2a\operatorname{sen}\left(\frac{2kx-2\omega t+\varphi }{2}\right)\cos \left(\frac{kx-\omega t-kx+\omega t-\varphi}{2}\right)\\[5pt]
y(x,t)=2a\operatorname{sen}\left(kx-\omega t+\frac{\varphi}{2}\right)\cos \left(-{\frac{\varphi }{2}}\right)
\end{gather}
\]
o cosseno é uma função par,
\( f(x)=f(-x) \),
temos
\( \cos \left(-{\frac{\varphi }{2}}\right)=\cos \left(\frac{\varphi}{2}\right) \)
\[
\begin{gather}
y(x,t)=2a\cos \left(\frac{\varphi}{2}\right)\operatorname{sen}\left(kx-\omega t+\frac{\varphi}{2}\right)
\end{gather}
\]
fazendo a definição
\( A\equiv 2a\cos \left(\frac{\varphi }{2}\right) \)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{y(x,t)=A\operatorname{sen}\left(kx-\omega t+\frac{\varphi }{2}\right)}
\end{gather}
\]
Observação: A amplitude A da onda resultante da superposição vai depender da
diferença de fase φ dessa ondas.
Assim a amplitude será máxima para
Figura 2
A partir desse ponto, enquanto a diferença de fase entre as ondas aumenta, a amplitude da onda formada pela superposição vai diminuindo, na Figura 3 vemos dois exemplos quando a diferença de fase vale \( \varphi =\frac{2\pi }{5} \) e \( \varphi =\frac{3\pi }{5} \).
Figura 3
A amplitude da onda formada, pela superposição, vai diminuindo até que para uma determinada diferença de fase ela será igual à amplitude das duas ondas que se superpõem, isso acontece quando
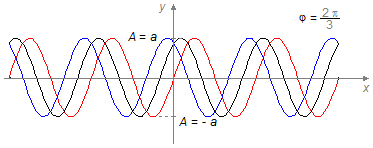Figura 4
Continuando o aumento da diferença de fase entre as ondas, a resultante da superposição passa a ter uma amplitude menor que a amplitude das ondas que se superpõem, Figura 5 para uma diferença de fase de \( \varphi =\frac{4\pi }{5} \).
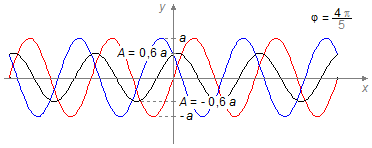Figura 5
Aumentando ainda mais a diferença de fase a amplitude deve continuar a diminuir até atingir um valor nulo, A = 0, isto ocorre quando a diferença de fase é igual a
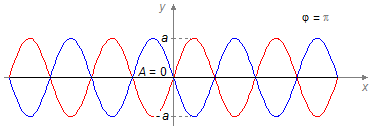Figura 6
\[
\begin{gather}
A=2a\cos \left(\frac{\varphi }{2}\right)
\end{gather}
\]
o termo 2a é constante, o módulo do cosseno varia de 0 a 1.Assim a amplitude será máxima para
\[
\begin{gather}
A=2a\underbrace{\cos \left(\frac{\varphi }{2}\right)}_{1}\Rightarrow A=2a
\end{gather}
\]
isso acontece quando o ângulo da diferença de fase é igual a
\[
\begin{gather}
2a\cos \left(\frac{\varphi }{2}\right)=2a\\[5pt]
\cos\left(\frac{\varphi }{2}\right)=\frac{2a}{2a}\\[5pt]
\cos \left(\frac{\varphi}{2}\right)=1\\[5pt]
\frac{\varphi }{2}=\arccos 1
\end{gather}
\]
os arcos para os quais o cosseno vale um são aqueles iguais a 0, 2π, 4π, 6π,...,2nπ,
\[
\qquad\qquad\qquad\qquad\quad
\begin{array}{c}
\dfrac{\varphi }{2}=2n\pi & \phantom{} & \phantom{} \\
\varphi =2.2n\pi & \phantom{} & \phantom{} \\
\varphi =4n\pi & \text{,} & n=0,1,2,3,...
\end{array}
\]
Neste caso as duas ondas não apresentam diferença de fase (estão em fase φ = 0), ambas
coincidem e produzem uma onda resultante da superposição com máxima amplitude, o dobro das ondas
originais (Figura 2).
A partir desse ponto, enquanto a diferença de fase entre as ondas aumenta, a amplitude da onda formada pela superposição vai diminuindo, na Figura 3 vemos dois exemplos quando a diferença de fase vale \( \varphi =\frac{2\pi }{5} \) e \( \varphi =\frac{3\pi }{5} \).
A amplitude da onda formada, pela superposição, vai diminuindo até que para uma determinada diferença de fase ela será igual à amplitude das duas ondas que se superpõem, isso acontece quando
\[
\begin{gather}
2a\cos \left(\frac{\varphi }{2}\right)=a\\[5pt]
\cos\left(\frac{\varphi }{2}\right)=\frac{\cancel{a}}{2\cancel{a}}\\[5pt]
\cos \left(\frac{\varphi}{2}\right)=\frac{1}{2}\\[5pt]
\frac{\varphi }{2}=\arccos\frac{1}{2}
\end{gather}
\]
o arco para o qual o cosseno vale
\( \frac{1}{2} \),
considerando apenas o primeiro quadrante do círculo trigonométrico, é igual a
\( \frac{\pi }{3} \)
\[
\begin{gather}
\frac{\varphi }{2}=\frac{\pi }{3}\\[5pt]
\varphi =\frac{2\pi}{3}
\end{gather}
\]
na Figura 4, vemos que a onda resultante da superposição (em preto) tem a mesma amplitude que as ondas que
se superpõem.
Continuando o aumento da diferença de fase entre as ondas, a resultante da superposição passa a ter uma amplitude menor que a amplitude das ondas que se superpõem, Figura 5 para uma diferença de fase de \( \varphi =\frac{4\pi }{5} \).
Aumentando ainda mais a diferença de fase a amplitude deve continuar a diminuir até atingir um valor nulo, A = 0, isto ocorre quando a diferença de fase é igual a
\[
\begin{gather}
2a\cos \left(\frac{\varphi }{2}\right)=0\\[5pt]
\cos\left(\frac{\varphi }{2}\right)=\frac{0}{2a}\\[5pt]
\cos \left(\frac{\varphi}{2}\right)=0\\[5pt]
\frac{\varphi }{2}=\arccos 0
\end{gather}
\]
os arcos para os quais o cosseno vale zero são aqueles iguais a
\( \frac{\pi }{2},\frac{3\pi }{2},\frac{5\pi }{2},...,\frac{(2n+1)\pi}{2},... \)
\[
\qquad\qquad\qquad\qquad\quad
\begin{array}{c}
\dfrac{\varphi}{2}=\dfrac{(2n+1)\pi }{2} & \phantom{} & \phantom{} \\
\varphi=\cancel{2}.\dfrac{(2n+1)\pi}{\cancel{2}} & \phantom{} & \phantom{} \\
\varphi=(2n+1)\pi & \text{,} & n=0,1,2,3,...
\end{array}
\]
Na Figura 6 temos duas ondas com diferença de fase de
\( \varphi =\pi \),
as duas ondas produzem uma resultante que não oscila, tendo amplitude nula em toda a sua extensão.
publicidade
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .