Exercício Resolvido de Momento de Inércia
publicidade
Demonstre o Teorema dos Eixos Paralelos.
Esquema do problema:
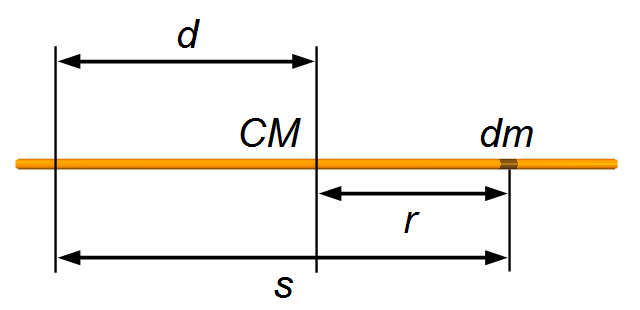
Na Figura 1, dm é um elemento de massa da barra, r é a distância do elemento de massa até
o eixo perpendicular ao centro de massa da barra, s é a distância do elemento de massa
até um eixo paralelo ao eixo que passa pelo centro de massa e d é a distância entre os
dois eixos.
Solução
Pela Figura 1 podemos escrever
\[
\begin{gather}
s=r+d \tag{I}
\end{gather}
\]
O momento de inércia em relação ao eixo que passa pelo centro de massa é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I_{CM}=\int r^{2}\;dm} \tag{II}
\end{gather}
\]
O momento de inércia em relação a um eixo paralelo ao eixo que passa pelo centro de massa é dado por
\[
\begin{gather}
I=\int s^{2}\;dm \tag{III}
\end{gather}
\]
substituindo a expressão (I) na expressão (III)
\[
I=\int (r+d)^{2}\;dm
\]
Desenvolvendo o integrando pelo Produto Notável
\( (a+b)^{2}=a^{2}+2 ab+b^{2} \)
\[
I=\int r^{2}+2 rd+d^{2}\;dm
\]
a integral da soma de funções é igual soma das integrais
\[
I=\int r^{2}\;dm+\int 2 rd\;dm+\int d^{2}\;dm
\]
A primeira integral representa o momento de inércia em relação ao eixo que passa pelo centro de massa
dada pela expressão (I). Na segunda integral o termo 2d é constante e na terceira integral
d2 é constante, colocando esses termos para fora da integral
\[
I=I_{CM}+2d\int r\;dm+d^{2}\int dm
\]
Na integral
\( \int r\;dm=0 \),
todos os elementos de massa multiplicados pela distância e somados são iguais a zero em relação ao
centro de massa do corpo.
Observação:
\( \int r\;dm=0 \):

Figura 2

Figura 3
As distâncias das massas ao Centro de massa são diferentes (rm > rM), mas as massas também são diferentes (m < M), isto faz com que os produtos rmm e rMM sejam iguais e somem zero.
Um outro sistema formado por três massas diferentes com valores m1, m2 e m3 e colocadas à distâncias r1 r2 e r3 do centro de massa do sistema. Adotamos um sistema de referência fixo no centro de massa. Decompondo os vetores posição na direções x e y, e calculando o produto das massas pela distância ao centro de massa ao longo das direções x e y e somando os resultados (Figuras 4-A e 4-B)
 Figura 4
Figura 4
As distâncias das massas ao centro de massa são diferentes, mas as massas também são diferentes, isto faz com que os produtos rimi nas direções x e y sejam iguais e somem zero.
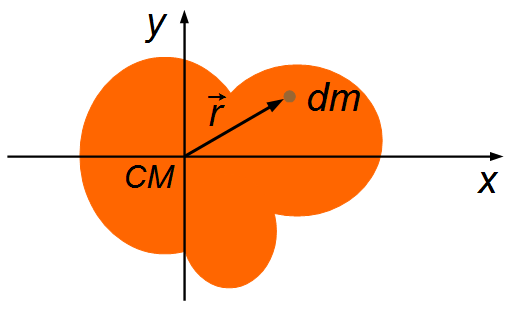
Figura 5
Temos um sistema formado por duas massas iguais a m e colocadas a mesma distância r do
centro de massa do sistema. Adotamos um sistema de referência fixo no centro de massa.
Calculando o produto das massas pela distância ao centro de massa e somando os resultados
(Figura 2)

Figura 2
\[
\sum_{i}r_{i}m_{1}=rm+(-r)m=rm-rm=0
\]
Temos um outro sistema formado por duas massas diferentes com valores m e M e colocadas
à distâncias rm e rM do centro de massa do sistema.
Adotamos um sistema de referância fixo no centro de massa. Calculando o produto das massas pela
distância ao centro de massa e somando os resultados (Figura 3)

Figura 3
\[
\sum_{i}r_{i}m_{1}=r_{m}m+(-r_{M})M=r_{m}m-r_{M}M=0
\]
As distâncias das massas ao Centro de massa são diferentes (rm > rM), mas as massas também são diferentes (m < M), isto faz com que os produtos rmm e rMM sejam iguais e somem zero.
Um outro sistema formado por três massas diferentes com valores m1, m2 e m3 e colocadas à distâncias r1 r2 e r3 do centro de massa do sistema. Adotamos um sistema de referência fixo no centro de massa. Decompondo os vetores posição na direções x e y, e calculando o produto das massas pela distância ao centro de massa ao longo das direções x e y e somando os resultados (Figuras 4-A e 4-B)
\[
\begin{split}
\sum_{i}r_{xi}m_{i} &=-r_{1x}m_{1}+(-r_{2x})m_{2}+r_{3x}m_{3}=\\
&=-r_{1x}m_{1}-r_{2x}m_{2}+r_{3x}m_{3}=0
\end{split}
\]
\[
\begin{split}
\sum_{i}r_{yi}m_{i} &=r_{1y}m_{1}+(-r_{2y})m_{2}+0.m_{3}=\\
&=r_{1y}m_{1}-r_{2y}m_{2}+0=0
\end{split}
\]

As distâncias das massas ao centro de massa são diferentes, mas as massas também são diferentes, isto faz com que os produtos rimi nas direções x e y sejam iguais e somem zero.
Para um corpo rígido de massa M, consideramos um elemento de massa dm dado pelo vetor
posição r em relação ao centro de massa do sistema. Adotamos um sistema de referência
fixo no centro de massa. Como temos uma distribuição de massa contínua passamos da somatória
para a integral. A integração sobre todos os elementos de massa será igual a zero (Figura 5)
\[
\int r\;dm=0
\]

Figura 5
A integral \( \int_{0}^{M}dm=M \), representa a massa total do corpo.
O momento de inércia do corpo em relação a um eixo paralelo ao eixo que passa pelo centro de massa será
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{I=I_{CM}+Md^{2}} \tag{Q.E.D.}
\end{gather}
\]
Observação: Q.E.D é a abreviação da expressão em latim Quod Erat Demonstrandum que
significa Como Queríamos Demonstrar.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .