Exercício Resolvido de Dinâmica das Rotações
publicidade
Uma máquina de Atwood possui massas mA e mB, onde a massa B é
maior que a massa A, ligadas por uma corda ideal, inextensível e de massa desprezível, através de
uma polia de massa M e raio R. Determinar a aceleração do sistema, a tensão na corda que
liga as massas e a tensão na corda que prende o sistema ao teto.

Dados do problema:
- Massa do corpo A: mA;
- Massa do corpo B: mB;
- Massa da polia: M;
- Raio da polia: R;
- Adotando a aceleração da gravidade: g.
Como a massa do bloco B é maior que a massa do bloco A, o bloco B desce enquanto o
bloco A sobe, a massa da polia não é desprezível, ela possui um momento de inércia. A corda é
ideal, portanto, a aceleração é a mesma para todo o conjunto (Figura 1).
Como a polia está girando a somatória dos torques em relação ao eixo da polia não é nula. As trações na corda de ambos os lados da polia não são iguais (Figura 1).
Como a polia está girando a somatória dos torques em relação ao eixo da polia não é nula. As trações na corda de ambos os lados da polia não são iguais (Figura 1).

Figura 1
Solução
Isolando os corpos e pesquisando as forças que atuam em cada um deles e aplicando a 2.ª Lei de Newton.
Para os blocos:
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{F}=m\mathbf{a}} \tag{I}
\end{gather}
\]
Para a polia:
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{N}=I\mathbf{\alpha}} \tag{II}
\end{gather}
\]
- Corpo A:
Adotando o sentido positivo no mesmo sentido da aceleração do bloco A (para cima – Figura 2)
- TA: tensão na corda;
- PA: força peso do bloco A.
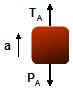
Figura 2
Aplicando a expressão (I)
\[
\begin{gather}
{\mathbf{T}}_{A}-{\mathbf{P}}_{A}=m_{A}\mathbf{a} \tag{III}
\end{gather}
\]
a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{P}=m\mathbf{g}} \tag{IV}
\end{gather}
\]
para o corpo A
\[
\begin{gather}
{\mathbf{P}}_{A}=m_{A}\mathbf{g} \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (III)
\[
{\mathbf{T}}_{A}-m_{A}\mathbf{g}=m_{A}\mathbf{a}
\]
em módulo
\[
\begin{gather}
T_{A}-m_{A}g=m_{A}a \tag{VI}
\end{gather}
\]
- Corpo B:
Adotando o sentido positivo no mesmo sentido da aceleração do bloco B (para baixo – Figura 3)
- TB: tensão na corda;
- PB: força peso do bloco B.
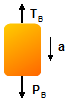
Figura 3
Aplicando a expressão (I)
\[
\begin{gather}
{\mathbf{P}}_{B}-{\mathbf{T}}_{B}=m_{B}\mathbf{a} \tag{VII}
\end{gather}
\]
usando a expressão (IV) para a força peso do corpo B
\[
\begin{gather}
{\mathbf{P}}_{B}=m_{B}\mathbf{g} \tag{VIII}
\end{gather}
\]
substituindo a expressão (VIII) na expressão (VII)
\[
m_{B}\mathbf{g}-{\mathbf{T}}_{B}=m_{B}\mathbf{a}
\]
em módulo
\[
\begin{gather}
m_{B}g-T_{B}=m_{B}a \tag{IX}
\end{gather}
\]
O torque de uma força é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{N}=\mathbf{r}\times{\mathbf{F}}} \tag{X}
\end{gather}
\]
No sistema da polia temos o vetor posição (r) dado pelo raio da polia e a força (F)
representada pela tensão (TA) na corda devido à massa mA,
(Figura 4-A). Aplicando a expressão (X)
\[
{\mathbf{N}}_{A}=\mathbf{r}\times{\mathbf{T}}_{A}
\]
Aplicando a regra da mão direita para o produto vetorial (levando o vetor r em direção ao vetor
TA – Figura 4-B) obtemos o vetor NA perpendicular a estes dois (Figura 4-C).
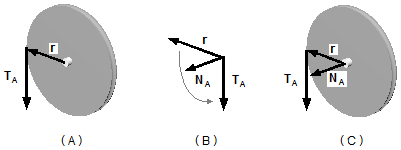
Os vetores r e TA são perpendiculares entre si, portanto, em módulo
\[
N_{A}=RT_{A}\operatorname{sen}\frac{\pi}{2}
\]
substituindo
\( \operatorname{sen}\frac{\pi}{2}=1 \)
\[
\begin{gather}
N_{A}=RT_{A} \tag{XI}
\end{gather}
\]
Para tensão (TB) na corda devido à massa mB, aplicando a expressão
(X), (Figura 5-A)
\[
{\mathbf{N}}_{B}=\mathbf{r}\times{\mathbf{T}}_{B}
\]
Aplicando a regra da mão direita para o produto vetorial (levando o vetor r em direção ao vetor
TB – Figura 5-B) obtemos o vetor NB perpendicular a estes
dois (Figura 5-C).

Os vetores r e TB são perpendiculares entre si, portanto, em módulo
\[
N_{B}=RT_{B}\operatorname{sen}\frac{\pi}{2}
\]
substituindo
\( \operatorname{sen}\frac{\pi}{2}=1 \)
\[
\begin{gather}
N_{B}=RT_{B} \tag{XII}
\end{gather}
\]
Para a polia
\[
{\mathbf{N}}_{A}+{\mathbf{N}}_{B}=I\mathbf{\alpha}
\]
adotando o sentido do torque NB como positivo escrevemos
\[
\begin{gather}
-N_{A}+N_{B}=I\alpha \tag{XIII}
\end{gather}
\]
O momento de inércia de um corpo é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I=\int {r^{2}\;dm}} \tag{XIV}
\end{gather}
\]
Consideremos a polia como um cilindro de altura pequena (h), Figura 6-A. Da expressão para a
densidade de massa (ρ) obtemos o elemento de massa dm
\[ \bbox[#99CCFF,10px]
{\rho =\frac{dm}{dV}}
\]
\[
dm=\rho \;dV
\]
o elemento de volume dV pode ser escrito como
\( dV=h\;dA \),
onde dA é um elemento de área da superfície da polia, então o elemento de massa fica escrito como
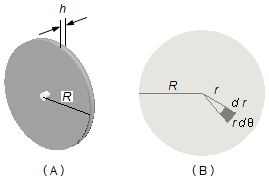
\[
\begin{gather}
dm=\rho h\;dA \tag{XV}
\end{gather}
\]
o elemento de área de ângulo dθ da polia (Figura 6-B), será
\[
\begin{gather}
dA=r\;dr\;d\theta \tag{XVI}
\end{gather}
\]
substituindo a expressão (XVI) na expressão (XV)
\[
\begin{gather}
dm=\rho hr\;dr\;d\theta \tag{XVII}
\end{gather}
\]
substituindo a expressão (XVII) na expressão (XIV)
\[
\begin{gather}
I=\int {r^{2}\rho hr\;dr\;d\theta }\\
I=\int{\rho hr^{3}\;dr\;d\theta }
\end{gather}
\]
a integração é feita sobre a superfície da polia (depende de duas variáveis r e θ) temos uma
integral dupla
\[
I=\int \int {\rho hr^{3}\;dr\;d\theta}
\]
Como a densidade de massa (ρ) e a largura da polia (h) são constantes elas podem “sair” da
integral, a integral depende de r e θ, podemos escrever
\[
I=\rho h\int \int {r^{3}\;dr\;d\theta}
\]
Os limites de integração serão de 0 a R em dr (ao longo do raio da polia) e de 0 e 2π em
dθ (uma volta completa na polia), as integrais podem ser separadas
\[
I=\rho h\int_{0}^{R}{r^{3}\;dr}\int_{0}^{{2\pi}}{d\theta}
\]
Integração de \( \displaystyle \int_{0}^{R}r^{3}\;dr \)
\[
\int_{0}^{R}r^{3}\;dr=\left.\frac{r^{3+1}}{3+1}\;\right|_{\;0}^{\;R}=\frac{R^{4}}{4}-\frac{0^{4}}{4}=\frac{R^{4}}{4}
\]
Integração de \( \displaystyle \int_{0}^{{2\pi}}d\theta \)
\[
\int _{0}^{{2\pi}}d\theta =\left.\theta \;\right|_{\;0}^{\;2\pi }=2\pi-0=2\pi
\]
\[
\begin{gather}
I=\rho h\frac{R^{4}}{4}2\pi \\
I=\rho h\pi R^{2}\frac{R^{2}}{2} \tag{XVIII}
\end{gather}
\]
A densidade da polia é dado por
\( \rho =\frac{M}{V} \),
onde M é a massa da polia dada no problema e V é o volume da polia de forma cilíndrica.
O volume de um cilindro é dado por
\( V=Ah \),
onde A é a área da polia de forma circular. A área de um circulo é dado por
\( A=\pi r^{2} \),
onde r é o raio da polia igual a R no problema. Assim o volume da polia vale
\( V=\pi R^{2}h \)
e da expressão da densidade podemos obter a massa da polia
\[
\begin{gather}
\rho =\frac{M}{\pi R^{2}h}\\
M=\pi R^{2}h\rho \tag{XIX}
\end{gather}
\]
substituindo a expressão (XIX) na expressão (XVIII) temos o momento de inércia da polia
\[
\begin{gather}
I=\frac{MR^{2}}{2} \tag{XX}
\end{gather}
\]
O bloco A sobe com aceleração a, como a corda é ideal cada ponto da corda também se desloca
com a mesma aceleração a, assim quando a corda passa pela polia, sem escorregamento, cada ponto da
corda se desloca junto com um ponto da polia (P1 e P'1,
P2 e P'2, P3 e P'3, ...), deste
modo a aceleração tangencial da polia e a mesma aceleração a do sistema (Figura 7).
A aceleração tangencial (Figura 8-A) é dada por
A aceleração tangencial (Figura 8-A) é dada por
\[ \bbox[#99CCFF,10px]
{\mathbf{a}=\mathbf{\alpha}\times{\mathbf{r}}}
\]

Figura 7
Para que o produto vetorial seja positivo devemos escolher o vetor da aceleração angular (α) para “dentro”, assim aplicando a regra da mão direita para o produto vetorial (levando o vetor α em direção ao vetor r – Figura 8-B) obtemos o vetor a perpendicular a estes dois (Figura 8-C).
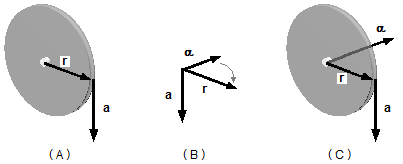
Observação: Se escolhêssemos o vetor aceleração angular para “fora” pela regra da mão
direita para o produto vetorial (levando o vetor α em direção ao vetor r – Figura 9)
obteríamos o vetor a perpendicular a estes dois com sentido para cima, isto não representaria a situação do
problema mostrada na Figura 8-A, onde sabemos que a aceleração tangencial do lado do bloco B está para
baixo.
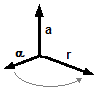
Figura 9
Os vetores r e a são perpendiculares entre si, portanto, em módulo
\[
a=\alpha R\operatorname{sen}\frac{\pi}{2}
\]
substituindo
\( \operatorname{sen}\frac{\pi}{2}=1 \)
\[
\begin{gather}
a=\alpha R\\
\alpha =\frac{a}{R} \tag{XXI}
\end{gather}
\]
substituindo as expressões (XI), (XII), (XX) e (XXI) na expressão (XIII)
\[
\begin{gather}
-RT_{A}+RT_{B}=\frac{MR^{2}}{2}\frac{a}{R}\\[5pt]
-RT_{A}+RT_{B}=\frac{MR}{2}a\\[5pt]
-T_{A}+T_{B}=\frac{Ma}{2} \tag{XXII}
\end{gather}
\]
As expressões (VI), (IX) e (XXII) formam um sistema de três equações a três incógnitas (a,
TA e TB)
\[
\left\{
\begin{matrix}
\;T_{A}-m_{A}g=m_{A}a\\
\;m_{B}g-T_{B}=m_{B}a\\
\;-T_{A}+T_{B}=\dfrac{Ma}{2}
\end{matrix}
\right.
\]
somando as três equações
\[
\begin{gather}
\frac{
\begin{matrix}
\;T_{A}-m_{A}g=m_{A}a\\
\;m_{B}g-T_{B}=m_{B}a\\
\;-T_{A}+T_{B}=\dfrac{Ma}{2}
\end{matrix}}
{m_{B}g-m_{A}g=m_{A}a+m_{B}a+\dfrac{Ma}{2}}\\
(m_{B}-m_{A})g=\left(m_{A}+m_{B}+\frac{M}{2}\right)a\\[5pt]
a=\frac{(m_{\text{B}}-m_{A})g}{\left(m_{A}+m_{B}+\dfrac{M}{2}\right)}.\frac{2}{2}\\[5pt]
a=\frac{2g(m_{B}-m_{A})}{2m_{A}+2m_{B}+2\dfrac{M}{2}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a=\frac{2g(m_{B}-m_{A})}{2m_{A}+2m_{B}+M}}
\]
Substituindo este valor na primeira equação do sistema temos o valor da tração na corda devido ao bloco
A
\[
\begin{gather}
T_{A}-m_{A}g=m_{A}\frac{2g(m_{B}-m_{A})}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}=m_{A}g+\frac{2m_{A}m_{B}g-2m_{A}^{2}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}=\frac{m_{A}g(2m_{A}+2m_{B}+M)+2m_{A}m_{B}g-2m_{A}^{2}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}=\frac{2m_{A}^{2}g+2m_{A}m_{B}g+Mm_{A}g+2m_{A}m_{B}g-2m_{A}^{2}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}=\frac{4m_{A}m_{B}g+Mm_{A}g}{2m_{A}+2m_{B}+M}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{A}=\frac{m_{A}g(4m_{B}+M)}{2m_{A}+2m_{B}+M}}
\]
Substituindo o valor da aceleração na segunda equação do sistema temos o valor da tração na corda devido ao
bloco B
\[
\begin{gather}
m_{B}g-T_{B}=m_{B}\frac{2g(m_{B}-m_{A})}{2m_{A}+2m_{B}+M}\\[5pt]
T_{B}=m_{B}g-m_{B}\frac{2g(m_{B}-m_{A})}{2m_{A}+2m_{B}+M}\\[5pt]
T_{B}=m_{B}g-\frac{2m_{B}^{2}g-2m_{A}m_{B}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{B}=\frac{m_{B}g(2m_{A}+2m_{B}+M)-2m_{B}^{2}g+2m_{A}m_{B}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{B}=\frac{2m_{A}m_{B}g+2m_{B}^{2}g+Mm_{B}g-2m_{B}^{2}g+2m_{A}m_{B}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{B}=\frac{4m_{A}m_{B}g+Mm_{B}g}{2m_{A}+2m_{B}+M}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{B}=\frac{m_{B}g(4m_{A}+M)}{2m_{A}+2m_{B}+M}}
\]
A tensão na corda que sustenta o sistema no teto será a soma das tensões dos dois lados da polia (Figura 1)
\[
\begin{gather}
T_{A}+T_{B}=\frac{m_{A}g(4m_{B}+M)}{2m_{A}+2m_{B}+M}+\frac{m_{B}g(4m_{A}+M)}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}+T_{B}=\frac{m_{A}g(4m_{B}+M)+m_{B}g(4m_{A}+M)}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}+T_{B}=\frac{4m_{A}m_{B}g+Mm_{A}g+4m_{A}m_{B}g+Mm_{B}g}{2m_{A}+2m_{B}+M}\\[5pt]
T_{A}+T_{B}=\frac{8m_{A}m_{B}g+Mm_{A}g+Mm_{B}g}{2m_{A}+2m_{B}+M}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{A}+T_{B}=\frac{8m_{A}m_{B}+Mm_{A}+Mm_{B}}{2m_{A}+2m_{B}+M}g}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .