Exercício Resolvido de Dinâmica
publicidade
Uma partícula de massa m é lançada verticalmente para cima com velocidade inicial v0 e sobe sob ação de uma força de resistência proporcional a velocidade. Determinar:
a) A equação da velocidade em função do tempo;
b) A equação da posição em função do tempo;
c) A altura máxima atingida pela partícula.
Dados do problema:
- Massa da partícula: m;
- Velocidade inicial da partícula: v0;
- Constante de proporcionalidade da força de resistência: b.
Adotamos um sistema de referência orientado para cima com origem no ponto onde a partícula é lançada.
Atuam na partícula a força peso P e a força de resistência FR que se
opõem ao movimento (Figura 1).
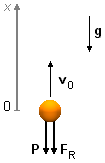
Figura 1
Solução
a) Aplicando a 2.ª Lei de Newton à partícula, escrevemos
\[ \bbox[#99CCFF,10px]
{\mathbf{F}=m\dot{{\mathbf{v}}}}
\]
\[
-{\mathbf{P}}-{\mathbf{F}}_{R}=m{\mathbf{\dot{v}}}
\]
a força peso é dada por
\[ \bbox[#99CCFF,10px]
{\mathbf{P}=m\mathbf{g}}
\]
a força de resistência é dada por
\[ \bbox[#99CCFF,10px]
{\mathbf{F}_{R}=b\mathbf{v}}
\]
substituindo estas expressões
\[
-mg\;\mathbf{j}-bv\;\mathbf{j}=m\dot{v}\;\mathbf{j}
\]
como só existe movimento em uma dimensão temos em módulo
\[
-mg-bv=m\dot{v}
\]
escrevendo
\( \dot{v}=\frac{dv}{dt} \)
e separando as variáveis
\[
\begin{gather}
-mg-bv=m\frac{dv}{dt}\\
m\frac{dv}{dt}=-b\left(\frac{mg}{b}+v\right)\\
\frac{dv}{\left(\dfrac{mg}{b}+v\right)}=-{\frac{b}{m}}dt
\end{gather}
\]
integrando a velocidade do lado esquerdo de v0 a v(t), a velocidade num
instante t qualquer, e do lado direito integrando o tempo de 0 a t, um instante qualquer
\[
\begin{gather}
\int_{v_{0}}^{{v(t)}}\frac{dv}{\left(\dfrac{mg}{b}+v\right)}=\int_{0}^{t}-\frac{b}{m}dt\\
\int_{v_{0}}^{{v(t)}}\frac{dv}{\left(\dfrac{mg}{b}+v\right)}=-{\frac{b}{m}}\int_{0}^{t}dt
\end{gather}
\]
Integração de \( \displaystyle \int_{v_{0}}^{{v(t)}}\frac{dv}{\left(\dfrac{mg}{b}+v\right)} \)
fazendo a mudança de variável
para \( v=v_{0} \)
temos \( u=\dfrac{mg}{b}+v_{0} \)
para \( v=v(t) \)
temos \( u=\dfrac{mg}{b}+v(t) \)
substituindo na integral
fazendo a mudança de variável
\[
\begin{align}
& u=\frac{mg}{b}+v\\
& \frac{du}{dv}=0+1\Rightarrow du=dv
\end{align}
\]
fazendo a mudança dos extremos de integração
para \( v=v_{0} \)
temos \( u=\dfrac{mg}{b}+v_{0} \)
para \( v=v(t) \)
temos \( u=\dfrac{mg}{b}+v(t) \)
substituindo na integral
\[
\begin{split}
\int_{\frac{{mg}}{b}+v_{0}}^{\frac{{mg}}{b}+v(t)}\frac{du}{u} &=\left.\ln u\right|_{\frac{{mg}}{b}+v_{0}}^{\frac{{mg}}{b}+v(t)}=\ln\left(\frac{mg}{b}+v(t)\right)-\ln\left(\frac{mg}{b}+v_{0}\right)=\\[5pt]
&=\ln\left(\frac{\dfrac{mg}{b}+v(t)}{\dfrac{mg}{b}+v_{0}}\right)=\ln\left(\frac{\dfrac{mg+bv(t)}{\cancel{b}}}{\dfrac{mg+bv_{0}}{\cancel{b}}}\right)=\\[5pt]
&=\ln\left(\frac{mg+bv(t)}{mg+bv_{0}}\right)
\end{split}
\]
Integração de \( \displaystyle \int_{0}^{t}dt \)
\[
\int_{0}^{t}dt=\left.t\;\right|_{\;0}^{\;t}=t-0=t
\]
\[
\begin{gather}
\ln\left(\frac{mg+bv(t)}{mg+bv_{0}}\right)=-{\frac{b}{m}}t\\[5pt]
\frac{mg+bv(t)}{mg+bv_{0}}=\operatorname{e}^{-{\frac{b}{m}}t}\\[5pt]
mg+bv(t)=(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}\\[5pt]
bv(t)=(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}-mg
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{v(t)=\frac{1}{b}(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}-\frac{mg}{b}}
\]
b) Sendo \( \dot{x}=\frac{dx}{dt} \), a equação da velocidade encontrada acima fica
\[
\begin{gather}
\frac{dx}{dt}=\frac{1}{b}(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}-\frac{mg}{b}\\
dx=\left[\frac{1}{b}(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}-\frac{mg}{b}\right]dt
\end{gather}
\]
integrando a posição do lado esquerdo de 0 a x(t), a posição num instante qualquer,
e do lado direito integrando o tempo de 0 a t, um instante qualquer. A integral da diferença é a
diferença das integrais
\[
\int_{0}^{{x(t)}}dx=\int_{0}^{t}\frac{1}{b}(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}dt-\int_{0}^{t}\frac{mg}{b}dt
\]
na primeira integral o termo
\( \dfrac{1}{b}(mg+bv_{0}) \)
e na segunda integral o termo
\( \dfrac{mg}{b} \)
são constantes e podem “sair' da integral
\[
\int_{0}^{{x(t)}}dx=\frac{1}{b}(mg+bv_{0})\int_{0}^{t}\;\operatorname{e}^{-{\frac{b}{m}}t}dt-\frac{mg}{b}\int_{0}^{t}dt
\]
Integração de \( \displaystyle \int_{0}^{{x(t)}}dx \)
\[
\int_{0}^{{x(t)}}dx=\left.x\;\right|_{\;0}^{\;x(t)}=x(t)-0=x(t)
\]
Integração de \( \displaystyle \int_{0}^{t}\;\operatorname{e}^{-{\frac{b}{m}}t}dt \)
fazendo a mudança de variável
para \( t=0 \)
temos \( u=-{\dfrac{b}{m}}.0=0 \)
para \( t=t \)
temos \( u=-{\dfrac{b}{m}}t \)
substituindo na integral
fazendo a mudança de variável
\[
\begin{align}
& u=-{\frac{b}{m}}t\\
& \frac{du}{dt}=-{\frac{b}{m}}\Rightarrow dt=-{\frac{m}{b}}du
\end{align}
\]
fazendo a mudança dos extremos de integração
para \( t=0 \)
temos \( u=-{\dfrac{b}{m}}.0=0 \)
para \( t=t \)
temos \( u=-{\dfrac{b}{m}}t \)
substituindo na integral
\[
\begin{split}
\int_{0}^{-{\frac{b}{m}}t}\;\operatorname{e}^{u}\left(-{\frac{m}{b}}\right)du &=-{\frac{m}{b}}\int_{0}^{-{\frac{b}{m}}t}\;\operatorname{e}^{u}du=-{\frac{m}{b}}\left.\;\operatorname{e}^{u}\;\right|_{0}^{-{\frac{b}{m}}t}=\\[5pt]
&=-\frac{m}{b}\left(\operatorname{e}^{-{\frac{b}{m}}t}-\operatorname{e}^{0}\right)=-{\frac{m}{b}}\left(\operatorname{e}^{-{\frac{b}{m}}t}-1\right)
\end{split}
\]
A integral em dt já foi calculada acima.
\[
x(t)=\frac{1}{b}(mg+bv_{0})\left[-{\frac{m}{b}}\left(\operatorname{e}^{-{\frac{b}{m}}t}-1\right)\right]-\frac{mg}{b}t
\]
\[ \bbox[#FFCCCC,10px]
{x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\operatorname{e}^{-{\frac{b}{m}}t}-1\right]-\frac{mg}{b}t}
\]
c) Quando a partícula atinge a altura máxima a velocidade dela se anula, v(t) = 0, substituindo este valor na expressão do item (a) obtemos o tempo de subida da partícula
\[
\begin{gather}
0=\frac{1}{b}(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}-\frac{mg}{b}\\[5pt]
\frac{1}{b}(mg+bv_{0})\;\operatorname{e}^{-{\frac{b}{m}}t}=\frac{mg}{b}\\[5pt]
\operatorname{e}^{-{\frac{b}{m}}t}=\frac{mg}{mg+bv_{0}}\\[5pt]
-{\frac{b}{m}}t=\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
t=-{\frac{m}{b}}\ln\left(\frac{mg}{mg+bv_{0}}\right)
\end{gather}
\]
substituindo este valor na expressão do item (b) temos a altura máxima da partícula
\[
\begin{gather}
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\exp\left(-{\frac{b}{m}}\left(-{\frac{m}{b}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\right)\right)-1\right]-\frac{mg}{b}\left(-{\frac{m}{b}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\right)\\[5pt]
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\exp\left(\frac{b}{m}\frac{m}{b}\ln\left(\frac{mg}{mg+bv_{0}}\right)\right)-1\right]+\frac{mg}{b}\frac{m}{b}\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\exp\left(\ln\left(\frac{mg}{mg+bv_{0}}\right)\right)-1\right]+\frac{m^{2}g}{b^{2}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\frac{mg}{mg+bv_{0}}-1\right]+\frac{m^{2}g}{b^{2}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\frac{mg-(mg+bv_{0})}{mg+bv_{0}}\right]+\frac{m^{2}g}{b^{2}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\frac{mg-mg-bv_{0}}{mg+bv_{0}}\right]+\frac{m^{2}g}{b^{2}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
x(t)=-{\frac{m}{b^{2}}}(mg+bv_{0})\left[\frac{-bv_{0}}{mg+bv_{0}}\right]+\frac{m^{2}g}{b^{2}}\ln\left(\frac{mg}{mg+bv_{0}}\right)\\[5pt]
x(t)=\frac{mv_{0}}{b}+\frac{m^{2}g}{b^{2}}\ln\left(\frac{mg}{mg+bv_{0}}\right)
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{x(t)=\frac{m}{b}\left[v_{0}+\frac{mg}{b}\ln\left(\frac{mg}{mg+bv_{0}}\right)\right]}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .