Exercício Resolvido de Dinâmica

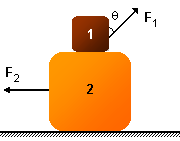
Um pequeno bloco de massa m₁ está apoiado sobre outro bloco maior de massa m₂, e este, sobre um plano horizontal. O bloco 1 é puxado com uma força que forma um ângulo θ com a vertical, e o bloco 2 é puxado na horizontal, o coeficiente de atrito estático entre os blocos, e entre o bloco e o plano são iguais a μ. Determinar os valores mínimos das forças com que os blocos devem ser puxados para que o movimento comece.

Dados do problema:

Massa do corpo 1: m₁;
Massa do corpo 2: m₂;
Ângulo da força 1: θ;
Coeficiente de atrito entre os blocos: μ;
Coeficiente de atrito entre o bloco e o plano: μ.

Esquema do problema:

Isolamos os corpos e pesquisando as forças em cada um deles.

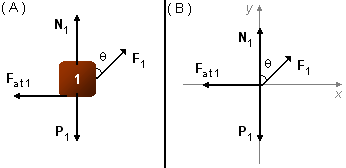
Bloco 1:

F₁: força com que o bloco 1 é puxado;
F_at1: força de atrito entre o bloco 1 e o bloco 2 devido à força 1;
P₁: força peso do bloco 1;
N₁: reação do contato com o bloco 2.

Figura 1

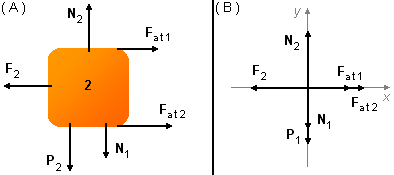
Bloco 2:

F₂: força com que o bloco 2 é puxado;
F_at2: força de atrito entre o bloco 2 e o plano;
F_at1: força de atrito entre o bloco 2 e o bloco 1;
P₂: força peso do bloco 2;
N₁: ação do bloco 1 no bloco 2,
N₂: reação do contato com o plano.

Figura 2

Solução

Como os blocos estão inicialmente em repouso temos a condição de que a somatória das forças que atuam sobre eles é zero

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum {\mathbf{F}}=0} \tag{I} \end{gather} \]

aplicando esta condição ao bloco 1 (Figura 1-B)

\[ {\mathbf{F}}_{1}+{\mathbf{F}}_{at 1}+{\mathbf{N}}_{1}+{\mathbf{P}}_{1}=0 \]

onde

\( {\mathbf{F}}_{1}=F_{1}\operatorname{sen}\theta\;\mathbf{i}+F_{1}\cos \theta\;\mathbf{j} \qquad\text{(II)} \)
\( {\mathbf{F}}_{at 1}=-\mu N_{1}\;\mathbf{i} \)
\( {\mathbf{N}}_{1}=N_{1}\;\mathbf{j} \)
\( {\mathbf{P}}_{1}=-m_{1}g\;\mathbf{j} \)

assim

\[ F_{1}\operatorname{sen}\theta \;\mathbf{i}+F_{1}\cos\theta \;\mathbf{j}-\mu N_{1}\;\mathbf{i}+N_{1}\;\mathbf{j}-m_{1}g\;\mathbf{j}=0 \tag{III} \]

Separando as componentes da equação (III)

\[ \begin{gather} \left\{ \begin{array}{l} F_{1}\operatorname{sen}\theta -\mu N_{1}=0\\ F_{1}\cos \theta+N_{1}-m_{1}g=0 \end{array} \right. \tag{IV} \end{gather} \]

isolando o valor de N₁ na segunda equação do sistema (IV) e substituindo na primeira equação

\[ \begin{gather} N_{1}=m_{1}g-F_{1}\cos \theta\\[10pt] F_{1}\operatorname{sen}\theta =\mu \left(m_{1}g-F_{1}\cos \theta\right)\\ F_{1}\operatorname{sen}\theta =\mu m_{1}g-\mu F_{1}\cos \theta\\ F_{1}\operatorname{sen}\theta +\mu F_{1}\cos \theta =\mu m_{1}g\\ F_{1}\left(\operatorname{sen}\theta +\mu \cos \theta\right)=\mu m_{1}g\\ F_{1}=\frac{\mu m_{1}g}{\operatorname{sen}\theta+\mu \cos \theta } \end{gather} \]

Substituindo este valor na expressão (II)) acima para o vetor F₁, para que o movimento comece a força aplicada deve ser maior que

\[ \bbox[#FFCCCC,10px] {{\mathbf{F}}_{1}=\frac{\mu m_{1}g}{\operatorname{sen}\theta +\mu \cos \theta}\left(\operatorname{sen}\theta \;\mathbf{i}+\cos \theta\;\mathbf{j}\right)} \]

Substituindo o valor de F₁ na segunda equação do sistema (IV) encontramos o valor da reação normal N₁

\[ \begin{gather} \frac{\mu m_{1}g}{\operatorname{sen}\theta +\mu \cos\theta }\cos \theta +N_{1}-m_{1}g=0\\[5pt] N_{1}=m_{1}g-\frac{\mu m_{1}g\cos\theta }{\operatorname{sen}\theta +\mu \cos \theta}\\[5pt] N_{1}=m_{1}g-\frac{\mu m_{1}g\cos \theta }{\operatorname{sen}\theta\left(1+\mu \dfrac{\cos \theta}{\operatorname{sen}\theta}\right)}\\[5pt] N_{1}=m_{1}g-\frac{\mu m_{1}g\operatorname{cotg}\theta}{1+\mu \operatorname{cotg}\theta} \tag{V} \end{gather} \]

Aplicando a condição (I) ao bloco 2 (Figura 2-B)

\[ {\mathbf{F}}_{2}+{\mathbf{F}}_{at 2}+{\mathbf{N}}_{2}+{\mathbf{P}}_{2}+{\mathbf{N}}_{1}+{\mathbf{F}}_{at 1}=0 \]

onde

\( {\mathbf{F}}_{2}=-F_{2}\;\mathbf{i} \qquad\text{(VI)} \)
\( {\mathbf{F}}_{at 2}=\mu N_{2}\;\mathbf{i} \)
\( {\mathbf{N}}_{1}=-N_{1}\;\mathbf{j} \)
\( {\mathbf{N}}_{2}=N_{2}\;\mathbf{j} \)
\( {\mathbf{P}}_{2}=-m_{2}g\;\mathbf{j} \)
\( {\mathbf{F}}_{at 1}=\mu N_{1}\;\mathbf{i} \)

assim

\[ -F_{2}\;\mathbf{i}+\mu N_{2}\;\mathbf{i}-N_{1}\;\mathbf{j}+N_{2}\;\mathbf{j}-m_{2}g\;\mathbf{j}+\mu N_{1}\;\mathbf{i}=0 \tag{VII} \]

Separando as componentes da equação (VII)

\[ \begin{gather} \left\{ \begin{array}{l} -F_{2}+\mu N_{2}+\mu N_{1}=0\\ -N_{1}+N_{2}-m_{2}g=0 \end{array} \right. \tag{VIII} \end{gather} \]

isolando o valor de N₂ na segunda equação do sistema (VIII) e substituindo na primeira equação

\[ \begin{gather} N_{2}=N_{1}+m_{2}g\\[10pt] -F_{2}+\mu\left(N_{1}+m_{2}g\right)+\mu N_{1}=0\\ F_{2}=\mu N_{1}+\mu m_{2}g+\mu N_{1}\\ F_{2}=2\mu N_{1}+\mu m_{2}g \tag{IX} \end{gather} \]

substituindo a expressão (V) na expressão (IX)

\[ \begin{gather} F_{2}=\mu \left[m_{2}g+2\left(m_{1}g-\frac{\mu m_{1}g\operatorname{cotg}\theta }{1+\mu \operatorname{cotg}\theta}\right)\right]\\[5pt] F_{2}=\mu \left[m_{2}g+2m_{1}g-2\frac{\mu m_{1}g\operatorname{cotg}\theta }{1+\mu \operatorname{cotg}\theta}\right] \end{gather} \]

Substituindo este valor na expressão (VI) acima para o vetor F₂, para que o movimento comece a força aplicada deve ser maior que

\[ \bbox[#FFCCCC,10px] {{\mathbf{F}}_{2}=-\mu\left[\left(m_{2}+2m_{1}\right)g-2\frac{\mu m_{1}g\operatorname{cotg}\theta }{1+\mu \operatorname{cotg}\theta}\right]\;\mathbf{i}} \]

Observação: Veja que em particular se \( \theta=\frac{\pi}{2} \) as soluções para as forças F₁ e F₂ se reduzem a

\[ \begin{gather} \mathbf{F}_{1}=\frac{\mu m_{1}g}{\cancelto{1}{\operatorname{sen}\frac{\pi}{2}} +\mu \cancelto{0}{\cos \frac{\pi}{2}}}\left(\cancelto{1}{\operatorname{sen}\frac{\pi}{2}} \;\mathbf{i}+\cancelto{0}{\cos \frac{\pi}{2}}\;\mathbf{j}\right)\\[5pt] \mathbf{F}_{1}=\mu m_{1}g \;\mathbf{i} \end{gather} \]

que é a força de atrito, então a força F₁ deve ser maior que esta para que o movimento comece.

\[ \begin{gather} \mathbf{F}_{2}=-\mu\left[\left(m_{2}+2m_{1}\right)g-2\frac{\mu m_{1}g \frac{\cancelto{0}{\cos \theta}}{\cancelto{1}{\operatorname{sen}\theta}} }{1+\mu \frac{\cancelto{0}{\cos \theta}}{\cancelto{1}{\operatorname{sen}\theta}}}\right]\;\mathbf{i}\\[5pt] \mathbf{F}_{2}=-\mu\left(m_{2}+2m_{1}\right)g\\[5pt] \mathbf{F}_{2}=-\mu\left(m_{2}+m_{1}+m_{1}\right)g\\[5pt] \mathbf{F}_{2}=-\mu\left(m_{2}+m_{1}\right)g+\mu m_{1}g \end{gather} \]

que é a força de atrito do sistema todo (m₁+m₂) sobre o solo e do atrtio entre os blocos (depende de m₁), então a força F₂ deve ser maior que esta para que o movimento comece.

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .