Exercício Resolvido de Dinâmica
publicidade
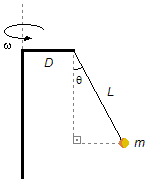
Um corpo de massa m está suspenso por uma corda, inextensível e de massa desprezível, na ponta de
um suporte em forma de L invertido verticalmente, com a barra horizontal medindo D,
conforme figura. Este conjunto gira em torno do eixo vertical do suporte. Sendo L o comprimento
da corda e g a aceleração local da gravidade, determine a velocidade angular com que o conjunto
deve girar para que o ângulo θ que a corda forma com a vertical seja 90°.
Dados do problema:
- Massa do corpo: m;
- Comprimento da corda: L;
- Comprimento do suporte horizontal: D;
- Aceleração local da gravidade: g.
A massa m está sob a ação da força peso (P) e da tração (T) na corda. Como o corpo
realiza um movimento circular ele está sob a ação da aceleração centrípeta (acp),
apontada radialmente para o centro da trajetória. O ângulo entre a tração na corda e a vertical passando
pelo corpo será θ, mesmo ângulo que temos entre a corda L e a vertical, pois estes ângulos
são alternos internos.

Solução
Desenhando as forças que atuam no corpo num sistema de eixos coordenados (Figura 2) e aplicando a
2.ª Lei de Newton
\[ \bbox[#99CCFF,10px]
{\mathbf{F}=m\mathbf{a}}
\]
\[
\begin{gather}
\mathbf{T}-\mathbf{P}=m\mathbf{a}\\
{\mathbf{T}}_{x}+{\mathbf{T}}_{y}-m\mathbf{g}=m\mathbf{a}\\
T_{x}\;\mathbf{i}+T_{y}\;\mathbf{j}-mg\;\mathbf{j}=m(a_{x}\;\mathbf{i}+a_{y}\;\mathbf{j})\\
T_{x}\;\mathbf{i}+T_{y}\;\mathbf{j}-mg\;\mathbf{j}=ma_{x}\;\mathbf{i}+ma_{y}\;\mathbf{j}
\end{gather}
\]
onde Tx e ax são as componentes da tração e da aceleração na direção
i e Ty e ay são as componentes da tração e da aceleração na direção
j.
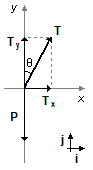
Figura 2
Separando as componentes:
- Direção i:
\[
\begin{gather}
T_{x}=ma_{x} \tag{I}
\end{gather}
\]
o módulo da componente Tx é dado por
\[
\begin{gather}
T_{x}=T\operatorname{sen}\theta \tag{II}
\end{gather}
\]
e a componente da aceleração ax é a aceleração centrípeta acp responsável
pelo corpo fazer a curva, substituindo esta aceleração e a expressão (II) na expressão (I)
\[
\begin{gather}
T\operatorname{sen}\theta =ma_{cp} \tag{III}
\end{gather}
\]
- Direção j:
\[
\begin{gather}
T_{y}-mg=ma_{y} \tag{IV}
\end{gather}
\]
o módulo da componente Ty é dado por
\[
\begin{gather}
T_{y}=T\cos \theta \tag{V}
\end{gather}
\]
com não existe movimento nesta direção a componente da aceleração é nula (ay = 0),
substituindo esta aceleração e a expressão (V) na expressão (IV)
\[
\begin{gather}
T\cos \theta -mg=m.0\\
T\cos \theta -mg=0\\
T\cos \theta=mg \tag{VI}
\end{gather}
\]
Dividindo a expressão (III) pela expressão (VI)
\[
\begin{gather}
\frac{T\operatorname{sen}\theta }{T\cos \theta}=\frac{ma_{cp}}{mg}\\
\operatorname{tg}\theta=\frac{a_{cp}}{g}\\
a_{cp}=g\operatorname{tg}\theta \tag{VII}
\end{gather}
\]
O módulo da aceleração centrípeta é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_{cp}=\frac{v^{2}}{r}} \tag{VIII}
\end{gather}
\]
a velocidade tangencial v é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r} \tag{IX}
\end{gather}
\]
substituindo a expressão (IX) na expressão (VIII)
\[
\begin{gather}
a_{cp}=\frac{(\omega r)^{2}}{r}\\
a_{cp}=\frac{\omega^{2}r^{\cancel{2}}}{\cancel{r}}\\
a_{cp}=\omega ^{2}r \tag{X}
\end{gather}
\]
onde r representa a distância do corpo ao eixo de rotação dado pela soma do comprimento do suporte
horizontal D e do deslocamento da massa R provocado pela rotação (Figura 3)
\[
\begin{gather}
r=D+R \tag{XI}
\end{gather}
\]
Da Figura 3 podemos escrever a distância R do deslocamento corpo como
\[
\begin{gather}
\operatorname{sen}\theta=\frac{R}{L}\\
R=L\operatorname{sen}\theta \tag{XII}
\end{gather}
\]
substituindo a expressão (XII) na expressão (XI)
\[
\begin{gather}
r=D+L\operatorname{sen}\theta \tag{XIII}
\end{gather}
\]
substituindo a expressão (XIII) na expressão (X) e esta na expressão (VII)
\[
\begin{gather}
\omega^{2}(D+L\operatorname{sen}\theta)=g\operatorname{tg}\theta \\
\omega^{2}=\frac{g\operatorname{tg}\theta}{(D+L\operatorname{sen}\theta )}\\
\omega=\left[\frac{g\operatorname{tg}\theta }{D+L\operatorname{sen}\theta}\right]^{\frac{1}{2}} \tag{XIV}
\end{gather}
\]

Figura 3
Queremos saber a velocidade angular para a qual o ângulo será \( \theta =90°=\frac{\pi}{2} \), para este ângulo o valor da tangente da expressão (XIV) tende ao infinito
\[
\lim _{\theta \to \frac{\pi}{2}}\omega =\lim_{\theta \to \frac{\pi}{2}}\left[\frac{g\operatorname{tg}\theta }{D+L\operatorname{sen}\theta}\right]^{\frac{1}{2}}=\left[\frac{g\operatorname{tg}\frac{\pi}{2}}{D+L\operatorname{sen}\frac{\pi}{2}}\right]^{\frac{1}{2}}=\left[\frac{g.\infty}{D+L.1}\right]^{\frac{1}{2}}=\infty
\]
\[ \bbox[#FFCCCC,10px]
{v=\infty}
\]
Observação: Na prática o ângulo nunca chega a 90°, pois para isso seria preciso uma velocidade
angular infinita, por mais rápido que se gire o corpo maior será o ângulo que ele forma com a vertical, no
entanto nunca ficará perfeitamente horizontal.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .