Exercício Resolvido de Potencial Elétrico
publicidade
Determine o potencial elétrico de um dipolo:
a ) Num ponto P qualquer, a uma distância r1 da carga positiva e a uma distância r2 da carga negativa;
b) Obtenha a expressão para pontos muito afastados do dipolo.
c) Determine o campo elétrico gerado pelo dipolo num ponto P muito distante do centro do dipolo em coordenadas polares.
d) Determine o vetor campo elétrico gerado pelo dipolo num ponto P muito distante do centro do dipolo em coordenadas cartesianas.
e) Determine o vetor campo elétrico gerado pelo dipolo para pontos da mediatriz muito afastados do dipolo;
f) Determine o vetor campo elétrico gerado pelo dipolo para pontos, sobre a reta que une as duas cargas, muito afastados do dipolo.
Solução
a) Consideremos uma carga q1 = +q num ponto x1 = +d e
uma carga q2 = −q num ponto x2 = −d, estas
cargas produzem um potencial elétrico num ponto P do espaço (Figura 1).
O potencial elétrico é dado pela soma do potencial elétrico gerado pelas cargas
O potencial elétrico é dado pela soma do potencial elétrico gerado pelas cargas
\[
\begin{gather}
V=\sum _{i}V_{i}\\
V=V_{1}+V_{2}\\
V=\frac{1}{4\pi\epsilon_{0}}\frac{q_{1}}{r_{1}}+\frac{1}{4\pi \epsilon_{0}}\frac{q_{2}}{r_{2}} \tag{I}
\end{gather}
\]
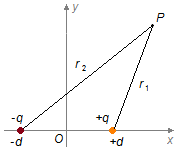
Figura 1
substituindo os valores das cargas
\[
\begin{gather}
V=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r_{1}}+\frac{1}{4\pi \epsilon_{0}}\frac{(-q)}{r_{2}}\\
V=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r_{1}}-\frac{1}{4\pi \epsilon_{0}}\frac{q}{r_{2}}\\
V=\frac{1}{4\pi \epsilon_{0}}q\left(\frac{1}{r_{1}}-\frac{1}{r_{2}}\right)
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{V=\frac{1}{4\pi \epsilon_{0}}q\left(\frac{r_{2}-r_{1}}{r_{1}r_{2}}\right)}
\]
b) Para o cálculo do potencial elétrico em pontos muito afastados do dipolo analisamos a região, próxima da origem do sistema, onde estão as cargas que formam o dipolo (Figura 2-A em destaque). Os segmentos de reta r1 e r2 são praticamente paralelos, então podemos traçar uma linha auxiliar que vai da carga positiva perpendicularmente ao segmento r2, determinando o ponto A, com isto temos o triângulo retângulo formado pelas cargas +q, −q e pelo ponto A, onde temos um cateto dado pela a diferença de caminhos entre os segmentos r1 e r2, dado por \( r_{2}-r_{1} \) e a hipotenusa será a distância entre as cargas dada por \( |\;d-(-d)\;|=2d \), então o cosseno do ângulo θ será
\[
\begin{gather}
\cos \theta \simeq\frac{r_{2}-r_{1}}{2d}\\
r_{2}-r_{1}\simeq 2d\cos \theta \tag{II}
\end{gather}
\]
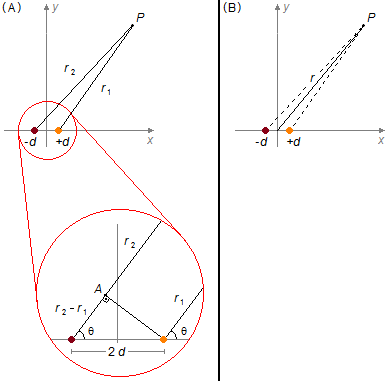
Como o ponto P está muito afastado os segmentos r1 e r2 têm praticamente o mesmo tamanho e são iguais ao segmento r que vai do ponto P à origem do sistema (Figura 2-B)
\[
\begin{gather}
r_{1}r_{2}\simeq r^{2} \tag{III}
\end{gather}
\]
Substituindo as expressões (II) e (III) na solução do item anterior
\[
V=\frac{1}{4\pi \epsilon_{0}}q\frac{2d\cos \theta}{r^{2}}
\]
Sendo o momento de dipolo dado por
\( p=2dq \)
\[ \bbox[#FFCCCC,10px]
{V=\frac{1}{4\pi \epsilon_{0}}\frac{p\cos \theta}{r^{2}}}
\]
c) O vetor campo elétrico é dado por menos o gradiente do potencial
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{E}=-\nabla V} \tag{IV}
\end{gather}
\]
onde
\( \nabla \)
é o operador nabla que em coordenadas polares é dado por
\( \left(\frac{\partial}{\partial r}\;{\mathbf{e}}_{r}+\frac{1}{r}\frac{\partial}{\partial \theta}\;{\mathbf{e}}_{\theta}\right) \), onde er e eθ são os vetores unitários nas direções r
e θ
\[
\begin{gather}
\mathbf{E}=-\left(\frac{\partial}{\partial r}\;{\mathbf{e}}_{r}+\frac{1}{r}\frac{\partial}{\partial \theta}\;{\mathbf{e}}_{\theta}\right)V\\
\mathbf{E}=-\left(\frac{\partial V}{\partial r}\;{\mathbf{e}}_{r}+\frac{1}{r}\frac{\partial V}{\partial \theta}\;{\mathbf{e}}_{\theta}\right)
\end{gather}
\]
Cálculo das derivadas parciais do potencial elétrico dado na solução do item anterior
\( V=\dfrac{1}{4\pi \epsilon_{0}}\dfrac{p\cos \theta}{r^{2}} \):
Derivada em r
Derivada em θ
\( V=\dfrac{1}{4\pi \epsilon_{0}}\dfrac{p\cos \theta}{r^{2}} \):
Derivada em r
\[
\begin{gather}
\frac{\partial V}{\partial r}=\frac{\partial}{\partial r}\left(\frac{1}{4\pi \epsilon_{0}}\frac{p\cos \theta}{r^{2}}\right)=\frac{1}{4\pi \epsilon_{0}}p\cos \theta \frac{\partial}{\partial r}\left(\frac{1}{r^{2}}\right)=\frac{1}{4\pi \epsilon_{0}}p\cos \theta \frac{\partial}{\partial r}\left(r^{-2}\right)\text{=}\\
\ \text{=}\frac{1}{4\pi \epsilon_{0}}p\cos \theta \left(-2r^{-2-1}\right)=-{\frac{1}{4\pi \epsilon_{0}}}\frac{2p\cos \theta}{r^{3}}
\end{gather}
\]
na derivada em r o valor de θ é constante e o cosseno sai da derivada.
Derivada em θ
\[
\frac{\partial V}{\partial \theta}=\frac{\partial}{\partial \theta}\left(\frac{1}{4\pi \epsilon_{0}}\frac{p\cos \theta}{r^{2}}\right)=\frac{1}{4\pi \epsilon_{0}}\frac{p}{r^{2}}\frac{\partial (\cos \theta )}{\partial \theta}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{r^{2}}(-\operatorname{sen}\theta)=\frac{-{1}}{4\pi \epsilon_{0}}\frac{p\operatorname{sen}\theta}{r^{2}}
\]
na derivada em θ o valor de r é constante e sai da derivada.
\[
\mathbf{E}=-\left(-{\frac{1}{4\pi \epsilon_{0}}}\frac{2p\cos \theta}{r^{3}}\;{\mathbf{E}}_{r}-\frac{1}{r}\frac{1}{4\pi\epsilon_{0}}\frac{p\operatorname{sen}\theta}{r^{2}}\;{\mathbf{E}}_{\theta}\right)
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{r^{3}}\left(2\cos \theta\;{\mathbf{E}}_{r}+\operatorname{sen}\theta\;{\mathbf{\text{e}}}_{\theta}\right)}
\]
e seu módulo será
\[
E=\sqrt{\left(\frac{1}{4\pi \epsilon_{0}}\frac{p}{r^{3}}\right)^{2}\left[(2\cos \theta)^{2}+(\operatorname{sen}\theta )^{2}\right]}
\]
\[ \bbox[#FFCCCC,10px]
{E=\frac{1}{4\pi \epsilon_{0}}\frac{p}{r^{3}}\sqrt{4\cos ^{2}\theta+\operatorname{sen}^{2}\theta}}
\]
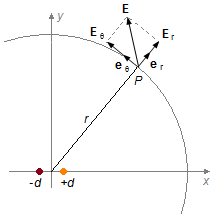
d) Da Figura 4 obtemos as seguintes relações
\[
\begin{gather}
r^{2}=x^{2}+y^{2} \tag{V}
\end{gather}
\]
\[
\begin{gather}
r=(x^{2}+y^{2})^{\frac{1}{2}} \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\cos \theta =\frac{x}{r} \tag{VII}
\end{gather}
\]
substituindo as expressões (V) e (VII) na solução do item (b)
\[
\begin{gather}
V=\frac{1}{4\pi \epsilon_{0}}\frac{p}{(x^{2}+y^{2})}\frac{x}{r} \tag{VIII}
\end{gather}
\]

Figura 4
substituindo a expressão (VI) na expressão (VIII)
\[
\begin{gather}
V=\frac{1}{4\pi \epsilon_{0}}\frac{p}{(x^{2}+y^{2})}\frac{x}{(x^{2}+y^{2})^{\frac{1}{2}}}\\
V=\frac{1}{4\pi\epsilon_{0}}\frac{px}{(x^{2}+y^{2})^{\frac{3}{2}}} \tag{IX}
\end{gather}
\]
Usamos novamente a expressão (IV) no valor do potencial elétrico acima para calcular o vetor campo elétrico,
em coordenadas cartesianas o operador nabla será dado por
\( \left(\frac{\partial}{\partial x}\;\mathbf{\text{i}}+\frac{\partial}{\partial y}\;\mathbf{j}\;\right) \),
onde i e j são os vetores unitários nas direções x e y
\[
\begin{gather}
\mathbf{E}=-\left(\;\frac{\partial}{\partial x}\;\mathbf{i}+\frac{\partial}{\partial y}\;\mathbf{j}\right)V\\
\mathbf{E}=-\left(\frac{\partial V}{\partial x}\;\mathbf{i}+\frac{\partial V}{\partial y}\;\mathbf{j}\right)
\end{gather}
\]
Cálculo das derivadas parciais do potencial elétrico dado pela expressão (IX)
\( V=\dfrac{1}{4\pi \epsilon_{0}}\dfrac{px}{(x^{2}+y^{2})^{\dfrac{3}{2}}} \):
Derivada em x:
A derivada em x é o quociente de duas funções, calculado pela regra
Reescrevendo
\( V=\dfrac{1}{4\pi \epsilon_{0}}\dfrac{px}{(x^{2}+y^{2})^{\dfrac{3}{2}}} \):
Derivada em x:
\[
\frac{\partial V}{\partial x}=\frac{\partial}{\partial x}\;\left[\frac{1}{4\pi \epsilon_{0}}\frac{px}{(x^{2}+y^{2})^{\frac{3}{2}}}\right]=\frac{1}{4\pi\epsilon_{0}}p\frac{\partial}{\partial x}\left[\frac{x}{(x^{2}+y^{2})^{\frac{3}{2}}}\right]
\]
na derivada em x o valor de y é constante.A derivada em x é o quociente de duas funções, calculado pela regra
\[
\left(\frac{f}{g}\right)^{'}=\frac{f'g-f\;g'}{g^{2}}
\]
com
\( f=x \)
e
\( g=(x^{2}+y^{2})^{\frac{3}{2}} \),
a função g é uma função composta
\( g[u(x)] \)
e sua derivada é dada pela regra da cadeia
\[
\frac{dg[u(x)]}{dx}=\frac{dg}{du}\frac{du}{dx}
\]
com
\( g(u)=u^{\frac{3}{2}} \)
e
\( u(x)=x^{2}+y^{2} \)
\[
\begin{align}
\frac{\partial}{\partial x}\left[\frac{x}{(x^{2}+y^{2})^{\frac{3}{2}}}\right]&=\left(\frac{f}{g}\right)^{'}=\frac{\left(\frac{df}{dx}\right)g-f\left[\left(\frac{dg}{du}\right)\left(\frac{du}{dx}\right)\right]}{g^{2}}\Rightarrow\\[5pt]
& \Rightarrow\frac{1.(x^{2}+y^{2})^{\frac{3}{2}}-x\left[\frac{3}{2}.(x^{2}+y^{2})^{\frac{3}{2}-1}.2x^{2-1}\right]}{\left[(x^{2}+y^{2})^{\frac{3}{2}}\right]^{2}}\Rightarrow\\[5pt]
& \Rightarrow\frac{(x^{2}+y^{2})^{\frac{3}{2}}-3(x^{2}+y^{2})^{\frac{1}{2}}x^{2}}{(x^{2}+y^{2})^{3}}\Rightarrow\\[5pt]
& \Rightarrow\frac{(x^{2}+y^{2})^{\frac{1}{2}}}{(x^{2}+y^{2})^{3}}(x^{2}+y^{2}-3x^{2})\Rightarrow\\[5pt]
& \Rightarrow\frac{(y^{2}-2x^{2})}{(x^{2}+y^{2})^{3}(x^{2}+y^{2})^{\frac{-{1}}{2}}}=\frac{(y^{2}-2x^{2})}{(x^{2}+y^{2})^{\frac{5}{2}}}
\end{align}
\]
\[
\frac{\partial V}{\partial x}=\frac{1}{4\pi \epsilon_{0}}p\frac{(y^{2}-2x^{2})}{(x^{2}+y^{2})^{\frac{5}{2}}}
\]
Derivada em y:
\[
\frac{\partial V}{\partial y}=\frac{\partial}{\partial y}\left[\frac{1}{4\pi \epsilon_{0}}\frac{px}{(x^{2}+y^{2})^{\frac{3}{2}}}\right]=\frac{1}{4\pi\epsilon_{0}}px\frac{\partial}{\partial x}\left[\frac{1}{(x^{2}+y^{2})^{\frac{3}{2}}}\right]
\]
na derivada em y o valor de x é constante.Reescrevendo
\[
f=\frac{1}{(x^{2}+y^{2})^{\frac{3}{2}}}=(x^{2}+y^{2})^{-{\frac{3}{2}}}
\]
a função f é uma função composta
\( f[u(x)] \)
e sua derivada é dada pela regra da cadeia
\[
\frac{df[u(x)]}{dx}=\frac{df}{du}\frac{du}{dx}
\]
com
\( f(u)=u^{\frac{-{3}}{2}} \)
e
\( u(x)=x^{2}+y^{2} \)
\[
\frac{\partial}{\partial x}\left[(x^{2}+y^{2})^{-{\frac{3}{2}}}\right]=\left[-{\frac{3}{2}}(x^{2}+y^{2})^{-{\frac{3}{2}}-1}\right]\left(2y^{2-1}\right)=-3y(x^{2}+y^{2})^{-{\frac{5}{2}}}=-{\frac{3y}{(x^{2}+y^{2})^{\frac{5}{2}}}}
\]
\[
\begin{gather}
\frac{\partial V}{\partial y}=\frac{1}{4\pi \epsilon_{0}}px\frac{\partial}{\partial x}\left[-{\frac{3y}{(x^{2}+y^{2})^{\frac{5}{2}}}}\right]\\
\frac{\partial V}{\partial y}=-{\frac{1}{4\pi \epsilon_{0}}}\frac{3pxy}{(x^{2}+y^{2})^{\frac{5}{2}}}
\end{gather}
\]
\[
\begin{gather}
\mathbf{E}=-\left[\frac{1}{4\pi \epsilon_{0}}p\frac{(y^{2}-2x^{2})}{(x^{2}+y^{2})^{\frac{5}{2}}}\;\mathbf{i}-\frac{1}{4\pi\epsilon_{0}}\frac{3pxy}{(x^{2}+y^{2})^{\frac{5}{2}}}\;\mathbf{j}\right]\\
\mathbf{E}=-{\frac{1}{4\pi\epsilon_{0}}}p\frac{(y^{2}-2x^{2})}{(x^{2}+y^{2})^{\frac{5}{2}}}\;\mathbf{i}+\frac{1}{4\pi\epsilon_{0}}\frac{3pxy}{(x^{2}+y^{2})^{\frac{5}{2}}}\;\mathbf{j}\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{(x^{2}+y^{2})^{\frac{5}{2}}}\left[-(y^{2}-2x^{2})\;\mathbf{i}+3xy\;\mathbf{j}\right]
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{(x^{2}+y^{2})^{\frac{5}{2}}}\left[(2x^{2}-y^{2})\;\mathbf{i}+3xy\;\mathbf{j}\right]}
\]
e seu módulo será
\[
\begin{gather}
E=\sqrt{\left(\frac{1}{4\pi \epsilon_{0}}\frac{p}{(x^{2}+y^{2})^{\frac{5}{2}}}\right)^{2}\left[(2x^{2}-y^{2})^{2}+(3xy)^{2}\right]}\\
E=\frac{1}{4\pi\epsilon_{0}}\frac{p}{(x^{2}+y^{2})^{\frac{5}{2}}}\sqrt{4x^{4}-4x^{2}y^{2}+y^{4}+9x^{2}y^{2}\;}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{E=\frac{1}{4\pi \epsilon_{0}}\frac{p}{(x^{2}+y^{2})^{\frac{5}{2}}}\sqrt{4x^{4}+5x^{2}y^{2}+y^{4}\;}}
\]
e) Fazendo x = 0 na solução do item anterior (Figura 5)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{(0^{2}+y^{2})^{\frac{5}{2}}}\left[(2.0^{2}-y^{2})\;\mathbf{i}+3.0.y\;\mathbf{j}\right]\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{(y^{2})^{\frac{5}{2}}}\left[-y^{2}\;\mathbf{i}\right]\\
\mathbf{E}=-{\frac{1}{4\pi\epsilon_{0}}}\frac{p}{y^{5}y^{-2}}\;\mathbf{i}
\end{gather}
\]
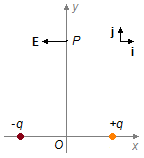
Figura 5
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=-{\frac{1}{4\pi \epsilon_{0}}}\frac{p}{y^{3}}\;\mathbf{i}}
\]
e seu módulo
\[ \bbox[#FFCCCC,10px]
{E=\frac{1}{4\pi \epsilon_{0}}\frac{p}{y^{3}}}
\]
f) Fazendo y = 0 na solução do item (d) (Figura 6)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\frac{p}{(x^{2}+0^{2})^{\frac{5}{2}}}\left[(2x^{2}-0^{2})\;\mathbf{i}+3.x.0\;\mathbf{j}\right]\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{(x^{2})^{\frac{5}{2}}}\left[2x^{2}\;\mathbf{i}\right]\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{2p}{x^{5}x^{-2}}\;\mathbf{i}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{2\pi \epsilon_{0}}\frac{p}{x^{3}}\;\mathbf{i}}
\]
e seu módulo
\[ \bbox[#FFCCCC,10px]
{E=\frac{1}{2\pi \epsilon_{0}}\frac{p}{x^{3}}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .