Exercício Resolvido de Potencial Elétrico
publicidade
Um disco de raio a está carregado uniformemente com uma carga Q. Calcule:
a) O potencial elétrico num ponto P sobre o eixo de simetria perpendicular ao plano do disco a uma distância z do seu centro;
b) O vetor campo elétrico no mesmo ponto.
a) O potencial elétrico num ponto P sobre o eixo de simetria perpendicular ao plano do disco a uma distância z do seu centro;
b) O vetor campo elétrico no mesmo ponto.
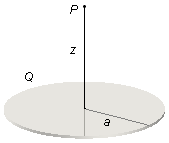
Dados do problema:
- Raio do disco: a;
- Carga do disco: Q;
- Distância ao ponto onde se quer o potencial elétrico: z.
A distância da origem ao ponto P é igual a z, a distância da origem a um elemento de carga
(dq) é igual a rq, e a distância de um elemento de carga até o ponto P é
r (Figura 1).
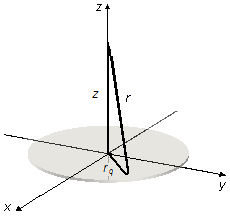
Solução
a) Aplicando o Teorema de Pitágoras ao triângulo retângulo Δrqzr
\[
\begin{gather}
r^{2}=r_{q}^{2}+z^{2}\\
r=\left(r_{q}^{2}+z^{2}\right)^{\frac{1}{2}} \tag{I}
\end{gather}
\]
O potencial elétrico é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{V=\frac{1}{4\pi \epsilon_{0}}\int {\frac{dq}{R}}} \tag{II}
\end{gather}
\]
Da expressão da densidade superficial de carga σ obtemos o elemento de carga dq
\[ \bbox[#99CCFF,10px]
{\sigma =\frac{dq}{dA}}
\]
\[
\begin{gather}
dq=\sigma \;dA \tag{III}
\end{gather}
\]
onde dA é um elemento de área de ângulo dθ do disco, assim pela Figura 2
\[
\begin{gather}
dA=r_{q}\;dr_{q}\;d\theta \tag{IV}
\end{gather}
\]
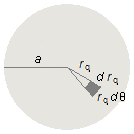
Figura 2
substituindo a expressão (IV) na expressão (III)
\[
\begin{gather}
dq=\sigma \;r_{q}\;dr_{q}\;d\theta \tag{V}
\end{gather}
\]
substituindo as expressões (I) e (V) na expressão (II), e como a integração é feita sobre a superfície do disco (depende de
duas variáveis rq e θ) temos uma integral dupla
\[
V=\frac{1}{4\pi \epsilon_{0}}\iint {\frac{\sigma\;r_{q}}{\left(r^{2}+z^{2}\right)^{\frac{1}{2}}}}\;dr_{q}\;d\theta
\]
Como a densidade de carga (σ) é constante e a integral não depende de z, depende de
rq e θ, elas podem “sair” da integral, podemos escrever
\[
V=\frac{\sigma}{4\pi \epsilon_{0}}\iint {\frac{r_{q}}{\left(r^{2}+z^{2}\right)^{\frac{1}{2}}}}\;dr_{q}\;d\theta
\]
Os limites de integração serão de 0 a a em drq (ao longo do raio do disco) e de 0 e 2π
em dq (uma volta completa no disco), e como não existem termos “cruzados “ em rq e θ
as integrais podem ser separadas
\[
V=\frac{\sigma }{4\pi \epsilon_{0}}\int_{0}^{a}{\frac{r_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{1}{2}}}}\;dr_{q}\;\int_{0}^{{2\pi}}d\theta
\]
Integral de \( \displaystyle \int_{0}^{a}{\dfrac{r_{q}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{1}{2}}}} \)
fazendo a mudança de variável
para rq = 0
temos \( u=0^{2}+z^{2}\Rightarrow u=z^{2} \)
para rq = a
temos \( u=a^{2}+z^{2} \)
fazendo a mudança de variável
\[
\begin{array}{l}
u=r_{q}^{2}+z^{2}\\
du=2r_{q}\;dr_{q}\;\Rightarrow \;dr_{q}=\dfrac{du}{2r_{q}}
\end{array}
\]
fazendo a mudança dos extremos de integração
para rq = 0
temos \( u=0^{2}+z^{2}\Rightarrow u=z^{2} \)
para rq = a
temos \( u=a^{2}+z^{2} \)
\[
\begin{gather}
\int_{{z^{2}}}^{{a^{2}+z^{2}}}{\frac{r_{q}}{u^{\frac{1}{2}}}\frac{du}{2r_{q}}}\Rightarrow\frac{1}{2}\int_{{z^{2}}}^{{a^{2}+z^{2}}}{\frac{1}{u^{\frac{1}{2}}}du}\Rightarrow\frac{1}{2}\left.\frac{u^{-{\frac{1}{2}+1}}}{-{\dfrac{1}{2}+1}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\frac{1}{2}\left.\frac{u^{\frac{-1+2}{2}}}{\dfrac{-{1+2}}{2}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\\
\qquad\Rightarrow\;\frac{1}{2}\left.\frac{u^{\frac{1}{2}}}{\dfrac{1}{2}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow \left.u^{\frac{1}{2}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow \sqrt{a^{2}+z^{2}\;}-\sqrt{z^{2}\;}\Rightarrow \sqrt{a^{2}+z^{2}\;}-z
\end{gather}
\]
Integral de \( \displaystyle \int_{0}^{{2\pi}}d\theta \)
\[
\int_{{0}}^{{2\pi}}\;d\theta =\left.\theta \;\right|_{\;0}^{\;2\pi}=2\pi -0=2\pi
\]
\[
V=\frac{\sigma }{\cancelto{2}{4}\cancel{\pi} \epsilon_{0}}\left(\sqrt{a^{2}+z^{2}\;}-z\right)\cancel{2}\cancel{\pi}
\]
\[ \bbox[#FFCCCC,10px]
{V=\frac{\sigma }{2\epsilon_{0}}\left(\sqrt{a^{2}+z^{2}\;}-z\right)}
\]
b) O vetor campo elétrico é dado por menos o gradiente do potencial
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=-\nabla V}
\]
onde
\( \nabla \)
é o operador nabla dado por
\( \left(\dfrac{\partial}{\partial x}\;\mathbf{i}+\dfrac{\partial}{\partial y}\;\mathbf{j}+\dfrac{\partial}{\partial z}\;\mathbf{k}\right) \).
\[
\begin{gather}
\mathbf{E}=-\left(\frac{\partial}{\partial x}\;\mathbf{i}+\frac{\partial}{\partial y}\;\mathbf{j}+\frac{\partial}{\partial z}\;\mathbf{k}\right)V\\
\mathbf{E}=-\left(\frac{\partial V}{\partial x}\;\mathbf{i}+\frac{\partial V}{\partial y}\;\mathbf{j}+\frac{\partial V}{\partial z}\;\mathbf{k}\right)
\end{gather}
\]
Derivada parcial do potencial em relação à x
\[
\frac{\partial V}{\partial x}=\frac{\partial}{\partial x}\left[\frac{\sigma }{2\epsilon_{0}}\;\left(\;\sqrt{\;a^{2}+z^{2}\;}-z\;\right)\right]
\]
a densidade de carga (σ), a permissividade do meio (ϵ0), o raio do aro (a) e a
distância (z) são constantes (a derivada é em relação à variável x, nesta direção z é constante),
portanto a derivada de uma constante é zero
\[
\frac{\partial V}{\partial x}=0
\]
Derivada parcial do potencial em relação à y
\[
\frac{\partial V}{\partial y}=\frac{\partial}{\partial y}\left[\frac{\sigma }{2\epsilon_{0}}\left(\sqrt{a^{2}+z^{2}\;}-z\right)\right]
\]
a densidade de carga (σ), a permissividade do meio (ϵ0), o raio do aro (a) e a
distância (z} são constantes (a derivada é em relação à variável y, nesta direção z é constante),
portanto a derivada de uma constante é zero
\[
\frac{\partial V}{\partial y}=0
\]
Derivada parcial do potencial em relação à z
\[
\frac{\partial V}{\partial z}=\frac{\partial}{\partial z}\left[\frac{\sigma }{2\epsilon_{0}}\left(\sqrt{a^{2}+z^{2}\;}-z\right)\right]
\]
a densidade de carga (σ) e a permissividade do meio (ϵ0) são constantes, portanto eles podem “sair”
da derivada
\[
\frac{\partial V}{\partial z}=\frac{\sigma }{2\epsilon_{0}}\frac{\partial}{\partial z}\left(\;\sqrt{\;a^{2}+z^{2}\;}-z\;\right)
\]
- o primeiro termo entre parênteses é uma função composta cuja derivada, pela regra da cadeia, é do tipo
\[
\frac{du[w(z)]}{dz}=\frac{du}{dw}\;\frac{dw}{dz}
\]
com
\( u(w)=w^{\frac{1}{2}} \)
e
\( w(z)=a^{2}+z^{2} \),
assim as derivadas serão
\[
\begin{array}{l}
\dfrac{du}{dw}=\dfrac{d\left(w^{\frac{1}{2}}\right)}{dw}=\dfrac{1}{2}w^{\frac{1}{2}-1}=\dfrac{1}{2}w^{\frac{1-2}{2}}=\dfrac{1}{2}w^{-{\frac{1}{2}}}=\dfrac{1}{2}\dfrac{1}{w^{\frac{1}{2}}}\\[10pt]
\dfrac{dw}{dz}=2z
\end{array}
\]
- o segundo termo entre parênteses é simplesmente
\[
\frac{d(z)}{dz}=1
\]
A derivada do potencial será
\[
\frac{\partial V}{\partial z}=\frac{\sigma }{2\epsilon_{0}}\left(\frac{1}{2}\frac{1}{\left(a^{2}+z^{2}\right)^{\frac{1}{2}}}\right)\left(2z\right)-1=\frac{\sigma}{2\epsilon_{0}}\left(\;\frac{z}{\sqrt{\;a^{2}+z^{2}}}-1\right)=\frac{\sigma z}{2\epsilon_{0}}\left(\frac{1}{\sqrt{\;a^{2}+z^{2}}}-\frac{1}{z}\right)
\]
\[
\mathbf{E}=-\left[\frac{\sigma}{2\epsilon_{0}}\left(\frac{z}{\sqrt{a^{2}+z^{2}\;}}-\frac{z}{z}\right)\mathbf{k}\right]
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{\sigma}{2\epsilon_{0}}\left(1-\frac{z}{\sqrt{a^{2}+z^{2}\;}}\right)\;\mathbf{k}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .