Exercício Resolvido de Lei de Gauss
publicidade
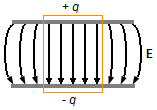
Considere dois planos paralelos, um carregado com carga +q e outro com carga −q de densidades superficiais constantes. Determine o módulo do campo elétrico para pontos entre os dois planos e para pontos fora dos planos.
Dados do problema:
- Carga do plano 1: +q;
- Carga do plano 2: −q.
As cargas positivas geram um campo elétrico de afastamento da placa E+ na direção vertical e com sentido para cima na face superior da placa e com sentido para baixo na face inferior. As cargas negativas geram um campo elétrico de aproximação da placa (E−) na direção vertical e com sentido para baixo na face superior da placa e com sentido para cima na face inferior (Figura 1-A).
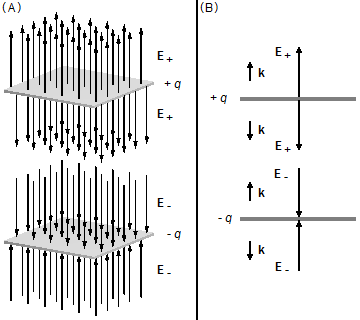
Vamos adotar um sistema de referência com o vetor unitário k para “fora” da placa, no mesmo sentido do campo elétrico para a placa carregada positivamente e com sentido contrário ao campo para a placa carregada negativamente (Figura 1-B).
Solução
Para a placa carregada positivamente vamos adotar uma superfície Gaussiana formada por um cilindro que atravessa o centro da placa, com as linhas do campo elétrico atravessando a superfície para fora (Figura 2-A).
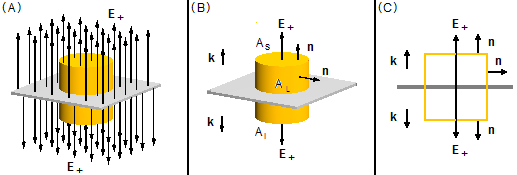
Seja um vetor unitário n perpendicular às faces superior, inferior e lateral do cilindro (AS, AI e AL), conforme Figuras 2-B e 2-C.
A Lei de Gauss no diz que
\[ \bbox[#99CCFF,10px]
{\oint_{A}\mathbf{E}.d\mathbf{A}=\frac{q}{\epsilon_{0}}}
\]
onde a integral é a soma das integrais sobre cada uma das áreas da superfície do cilindro
\[
\int_{A_{S}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{S}+\int_{A_{I}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{I}+\int_{A_{L}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{L}=\frac{q}{\epsilon_{0}}
\]
As áreas superior e inferior são iguais à área de um círculo
(AS=AI=AC)
\[
\begin{gather}
\int_{A_{C}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{C}+\int_{A_{C}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{C}+\int_{A_{L}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{L}=\frac{q}{\epsilon_{0}}\\
2\int_{A_{C}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{C}+\int_{A_{L}}{\mathbf{E}}_{\text{+}}.d\mathbf{A}_{L}=\frac{q}{\epsilon_{0}} \tag{I}
\end{gather}
\]
O vetor campo elétrico só possui componente na direção k, pode ser escrito como
\[
\begin{gather}
{\mathbf{E}}_{\text{+}}=E_{\text{+}}\;\mathbf{k} \tag{II}
\end{gather}
\]
O vetor elemento de área pode ser escrito como
\[
\begin{gather}
d\mathbf{A}=dA\;\mathbf{n} \tag{III}
\end{gather}
\]
substituindo as expressões (II) e (III) na expressão (I)
\[
\begin{gather}
2\int_{A_{C}}E_{\text{+}}\;\mathbf{k}.dA_{C}\;\mathbf{n}+\int_{A_{\text{L}}}E_{\text{+}}\;\mathbf{k}.dA_{L}\mathbf{n}=\frac{q}{\epsilon_{0}}\\
2\int_{A_{C}}E_{\text{+}}\;dA_{C}\;\underbrace{\mathbf{k}.\mathbf{n}}_{1}+\int_{A_{L}}E_{\text{+}}\;dA_{L}\;\underbrace{\mathbf{k}.\mathbf{n}}_{0}=\frac{q}{\epsilon_{0}}
\end{gather}
\]
Observação: Como k e n são vetores unitários, seus módulos são iguais a 1, e
como ambos estão na mesma direção e sentido nas faces superior e inferior o ângulo entre eles é nulo
(θ = 0)
\( \mathbf{k}.\mathbf{n}=|\;\mathbf{k}\;|\;|\;\mathbf{n}\;|\;\cos 0=1.1.1=1 \).
\[ \mathbf{k}.\mathbf{n}=|\;\mathbf{k}\;|\;|\;\mathbf{n}\;|\;\cos 0=1.1.1=1 \]
Para a face lateral do cilindro k é perpendicular a n
\( \left(\theta =\frac{\pi}{2}\right) \)
o produto escalar será
\( \mathbf{k}\mathbf{n}=|\;\mathbf{k}\;|\;|\;\mathbf{n}\;|\;\cos\frac{\pi }{2}=1.1.0=0 \).
\[ \mathbf{k}\mathbf{n}=|\;\mathbf{k}\;|\;|\;\mathbf{n}\;|\;\cos\frac{\pi }{2}=1.1.0=0 \]
\[
\begin{gather}
2\int_{A_{C}}E_{\text{+}}\;dA_{C}=\frac{q}{\epsilon_{0}} \tag{IV}
\end{gather}
\]
A densidade superficial de cargas é dada por
\[ \bbox[#99CCFF,10px]
{\sigma =\frac{q}{A}}
\]
\[
q=\sigma A \tag{V}
\]
onde A representa a área onde as cargas estão distribuídas internamente à superfície Gaussiana
(não toda a área da placa), e colocando o campo elétrico para fora da integral, substituindo a expressão (V)
na expressão (IV)
\[
2E_{\text{+}}\underbrace{\int_{A_{C}}dA_{C}}_{A}=\frac{\sigma A}{\epsilon_{0}}
\]
a integral da área do círculo é igual a área A da placa, interna à superficial Gaussiana, onde
estão distribuídas as cargas
\[
\begin{gather}
2E_{\text{+}}A=\frac{\sigma A}{\epsilon_{0}}\\
E_{\text{+}}=\frac{\sigma }{2\epsilon_{0}} \tag{VI}
\end{gather}
\]
Analogamente para a placa carregada negativamente temos a mesma superfície Gaussiana com a diferença
de que as linhas do campo elétrico atravessam a superfície para dentro (Figura 3-A).
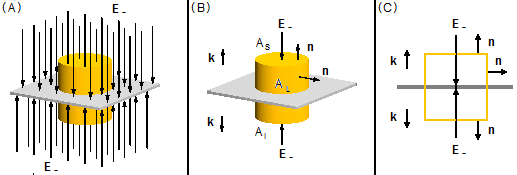
O vetor unitário (n) tem a mesma orientação do caso anterior, Figuras 3-B e 3-C.
Usando a Lei de Gauss novamente temos a mesma situação com a carga negativa da placa
\[
\int_{A_{S}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{S}+\int_{A_{I}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{I}+\int_{A_{L}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{L}=\frac{-q}{\epsilon_{0}}
\]
As áreas superior e inferior são igual a área de um círculo
(AS=AI=AC)
\[
\begin{gather}
\int_{A_{C}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{C}+\int_{A_{C}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{C}+\int_{A_{L}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{L}=-{\frac{q}{\epsilon_{0}}}\\
2\int_{A_{C}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{C}+\int_{A_{L}}{\mathbf{E}}_{\text{-}}.d\mathbf{A}_{L}=-{\frac{q}{\epsilon_{0}}} \tag{VII}
\end{gather}
\]
O vetor campo elétrico só possui componente na direção −k com sentido contrário à orientação, é
escrito como
\[
\begin{gather}
{\mathbf{E}}_{\text{-}}=-E_{\text{-}}\;\mathbf{k} \tag{VIII}
\end{gather}
\]
substituindo as expressões (III) e (VIII) na expressão (VII)
\[
\begin{gather}
2\int_{A_{C}}-E_{\text{-}}\;\mathbf{k}.dA_{C}\;\mathbf{n}+\int_{A_{L}}-E_{\text{-}}\;\mathbf{k}.dA_{L}\mathbf{n}=-{\frac{q}{\epsilon_{0}}}\\
-2\int_{A_{C}}E_{\text{-}}\;dA_{C}\;\underbrace{\mathbf{k}.\mathbf{n}}_{1}-\int_{A_{L}}E_{\text{-}}\;dA_{L}\;\underbrace{\mathbf{k}.\mathbf{n}}_{0}=-{\frac{q}{\epsilon_{0}}}\\
-2\int _{A_{C}}E_{\text{-}}\;dA_{C}=-{\frac{q}{\epsilon_{0}}\epsilon _{0}}\\
2\int_{A_{C}}E_{\text{-}}\;dA_{C}=\frac{q}{\epsilon_{0}} \tag{IX}
\end{gather}
\]
substituindo a expressão (V) na expressão (IX)
\[
2E_{\text{-}}\underbrace{\int_{A_{C}}dA_{C}}_{A}=\frac{\sigma A}{\epsilon_{0}}
\]
esta é a mesma integral calculada acima, o que nos leva ao mesmo resultado encontrado na expressão (VI)
\[
\begin{gather}
E_{\text{-}}=\frac{\sigma }{2\;\epsilon _{0}} \tag{X}
\end{gather}
\]
Entre as placas os campos elétricos devido às placas carregadas positiva e negativamente têm a mesma
direção e o mesmo sentido, assim o módulo do campo elétrico resultante(E) será dada pela soma das
expressões (VI) e (X)
\[
\begin{gather}
E=E_{\text{+}}+E_{\text{-}}\\
E=\frac{\sigma}{2\epsilon _{0}}+\frac{\sigma}{2\epsilon_{0}}\\
E=2\frac{\sigma}{2\epsilon_{0}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{E_{\text{-}}=\frac{\sigma}{\epsilon_{0}}}
\]
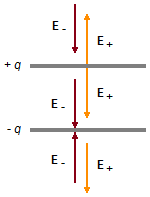
Figura 4
Na região fora das placas os campos elétricos têm sentidos opostos, assim o módulo do campo elétrico resultante será dada pela diferença das expressões (VI) e (X)
\[
\begin{gather}
E=E_{\text{+}}-E_{\text{-}}\\
E=\frac{\sigma}{2\epsilon_{0}}-\frac{\sigma }{2\epsilon_{0}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{E_{\text{-}}=0}
\]
Observação: Esta solução vale para pontos longe das bordas das placas e pequena
distância de separação entre elas, onde o campo elétrico é uniforme, região em destaque na Figura 5.
Próximo às bordas das placas o campo elétrico não é constante devido ao encurvamento das linhas do
campo elétrico, este é o chamado Efeito de Borda.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .