Exercício Resolvido de Lei de Gauss
publicidade
Determine o módulo do campo elétrico em todo o espaço gerado por uma esfera maciça carregada com uma carga Q distribuída uniformemente pelo seu volume.
Dados do problema:
- Carga da esfera: Q.
Vamos assumir que a esfera está carrega com uma carga positiva (Q > 0) e seu raio é igual a R.
Para determinar o módulo do campo elétrico em todo o espaço devemos considerar os pontos no interior da esfera, \( r\leqslant R \), e pontos no exterior da esfera (r > R), conforme Figura 1.
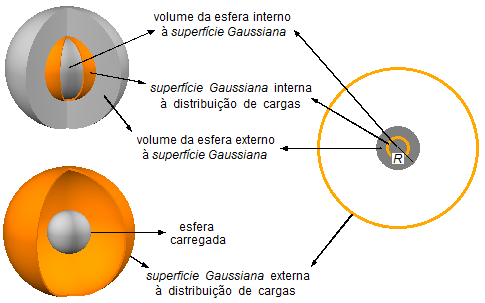
Consideramos uma superfície Gaussiana interna e outra superfície externa á esfera.
Solução
- Para \( r\;\leqslant \;R \):
Como a carga está distribuída pelo seu volume existem cargas no seu interior (Figura 2), pela
Lei de Gauss
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\oint_{A}{\mathbf{E}}.d\mathbf{A}=\frac{q}{\epsilon_{0}}} \tag{I}
\end{gather}
\]
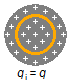
Figura 2
a Lei de Gauss nos diz que apenas a carga interna à superfície Gaussiana contribui para o campo elétrico
\[
\begin{gather}
\oint_{A}{\mathbf{E}}.d\mathbf{A}=\frac{1}{\epsilon_{0}}\int \rho \;dV \tag{II}
\end{gather}
\]
onde ρ é a densidade volumétrica de cargas e a integração é feita sobre o volume limitado pela
superfície Gaussiana.
A superfície Gaussiana que passa pelo ponto onde se deseja calcular o campo elétrico tem um raio
rs, a distribuição de cargas interna à superfície Gaussiana tem um raio
rq, como o ponto onde se deseja calcular o campo elétrico está no interior da
distribuição de cargas esses raios coincidem rs = rq = r
(Figura 3).
O campo elétrico se espalha radialmente a partir da distribuição de cargas na direção er, e em cada elemento de área dA, na superfície temos um vetor unitário n perpendicular à superfície e orientado para fora. Assim em cada ponto da superfície o vetor campo elétrico E e o vetor unitário n possuem a mesma direção e sentido (Figura 4).
O campo elétrico se espalha radialmente a partir da distribuição de cargas na direção er, e em cada elemento de área dA, na superfície temos um vetor unitário n perpendicular à superfície e orientado para fora. Assim em cada ponto da superfície o vetor campo elétrico E e o vetor unitário n possuem a mesma direção e sentido (Figura 4).
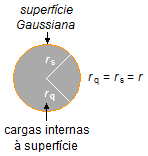
Figura 3
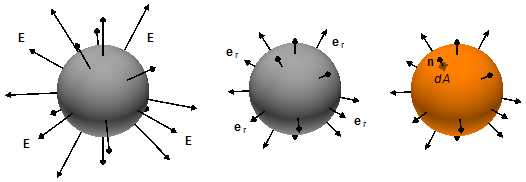
O vetor campo elétrico só possui componente na direção er pode ser escrito como
\[
\begin{gather}
\mathbf{E}=E\;{\mathbf{e}}_{r} \tag{III}
\end{gather}
\]
O vetor elemento de área pode ser escrito como
\[
\begin{gather}
d\mathbf{A}=dA\;\mathbf{n} \tag{IV}
\end{gather}
\]
substituindo as expressões (III) e (IV) na expressão (II)
\[
\begin{gather}
\oint_{A}E\;{\mathbf{E}}_{r}.dA\;\mathbf{n}=\frac{1}{\epsilon_{0}}\int \rho \;dV\\
\oint_{A}E\;dA\;\underbrace{{\mathbf{E}}_{r}.\mathbf{n}}_{1}=\frac{1}{\epsilon_{0}}\int \rho \;dV
\end{gather}
\]
Observação: Como er e n são vetores unitários seus módulos
são iguais a 1 e como ambos estão na mesma direção e sentido o ângulo entre eles é nulo
(θ = 0),
\( {\mathbf{e}}_{r}.\mathbf{n}=|\;{\mathbf{e}}_{r}\;|\;|\;\mathbf{n}\;|\;\cos0=1.1.1=1 \text{.}\)
\[ {\mathbf{e}}_{r}.\mathbf{n}=|\;{\mathbf{e}}_{r}\;|\;|\;\mathbf{n}\;|\;\cos0=1.1.1=1 \]
\[
\begin{gather}
\oint_{A}E\;dA=\frac{1}{\epsilon_{0}}\int \rho \;dV \tag{V}
\end{gather}
\]
A integral do lado esquerdo da igualdade na expressão (V) refere-se a superfície Gaussiana e é feita
sobre todos os elementos de área dA (Figura 5-A), a integral do lado direito da igualdade refere-se
a distribuição de cargas interna à superfície Gaussiana e é feita sobre todos os elementos de volume
dV (Figura 5-B).O elemento de área dA será
\[
\begin{gather}
dA=r_{s}\;d\theta \;r\operatorname{sen}\theta\;d\phi \\
dA=r_{s}^{2}\operatorname{sen}\theta \;d\theta\;d\phi \tag{VI}
\end{gather}
\]
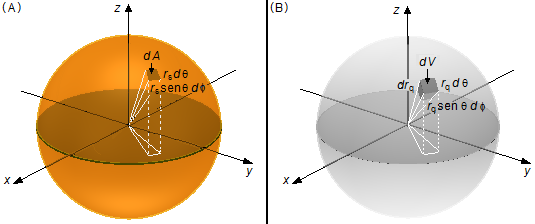
O elemento de volume dV será
\[
\begin{gather}
dV=r_{q}\;d\theta\;r_{q}\operatorname{sen}\theta \;d\phi\;dr_{q}\\
dV=r_{q}^{2}\operatorname{sen}\theta\;dr_{q}\;d\theta \;d\phi \tag{VII}
\end{gather}
\]
Substituindo as expressões (VI) e (VII) na expressão (V)
\[
\int Er_{s}^{2}\operatorname{sen}\theta \;d\theta \;d\phi=\frac{1}{\epsilon_{0}}\int \rho \;r_{q}^{2}\operatorname{sen}\theta\;dr_{q}\;d\theta \;d\phi
\]
Do lado esquerdo da igualdade a integral não depende do raio da superfície Gaussiana, assim E e
rs podem “sair” da integral, e como não existem termos “cruzados” em θ e ϕ as
integrais podem ser separadas. Do lado direito da igualdade a integral não depende da densidade volumétrica
de cargas, assim ρ pode “sair” da integral, e como não existem termos “cruzados” em rq,
θ e ϕ as integrais podem ser separadas.
\[
\begin{gather}
Er_{s}^{2}\int \operatorname{sen}\theta \;d\theta \int d\phi =\frac{\rho}{\epsilon_{0}}\int r_{q}^{2}\;dr_{q}\int\operatorname{sen}\theta \;d\theta \int d\phi \tag{VIII}
\end{gather}
\]
Do lado esquerdo da igualdade os limites de integração serão de 0 a π em dθ e de 0 e 2π em
dϕ (uma volta completa na base do hemisfério), conforme Figura 6-A, e temos
rs = r, lembrando da Figura 3 acima.
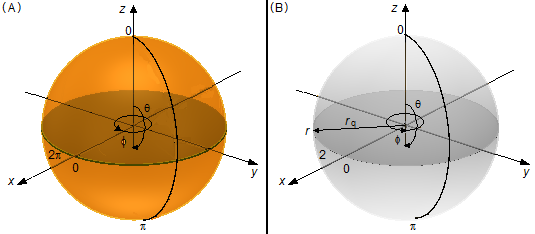
Do lado direito os limites de integração serão de 0 a π em dθ, de 0 e 2π em dϕ (uma volta completa na base do hemisfério) e de 0 a r em drq (Figura 6-B).
\[
Er^{2}\int_{0}^{\pi}\operatorname{sen}\theta \;d\theta \int_{0}^{{2\pi}}d\phi =\frac{\rho}{\epsilon_{0}}\int_{0}^{r}r_{q}^{2}\;dr_{q}\int_{0}^{\pi}\operatorname{sen}\theta \;d\theta \int_{0}^{{2\pi}}d\phi
\]
Integral de \( \displaystyle \int_{0}^{\pi}\operatorname{sen}\theta \;d\theta \)
\[
\begin{align}
\int_{0}^{\pi}\operatorname{sen}\theta \;d\theta & =\left.-\cos \theta \;\right|_{\;0}^{\;\pi}= -(\cos \pi -\cos0)= \\
& =-(-1-1)= -(-2)= 2
\end{align}
\]
Integral de \( \displaystyle \int_{0}^{{2\pi}}\;d\phi \)
\[
\int_{0}^{{2\pi}}\;d\phi =\left.\phi \;\right|_{\;0}^{\;2\pi}=2\pi-0=2\pi
\]
Integral de \( \displaystyle \int_{0}^{r}r_{q}^{2}\;dr_{q} \)
\[
\int_{0}^{r}r_{q}^{2}\;dr_{q}=\left.\frac{r_{q}^{2+1}}{2+1}\;\right|_{\;0}^{\;r}=\left.\frac{r_{q}^{3}}{3}\;\right|_{\;0}^{\;r}=\left(\frac{r^{3}}{3}-\frac{0^{3}}{3}\right)=\frac{r^{3}}{3}
\]
\[
\begin{gather}
E\cancel{r^{2}}\cancel{2}.\cancel{2}\cancel{\pi} =\frac{\rho}{\epsilon_{0}}\frac{r^{\cancelto{1}{3}}}{3}\cancel{2}.\cancel{2}\cancel{\pi}\\
E=\frac{\rho}{\epsilon_{0}}\frac{r}{3} \tag{IX}
\end{gather}
\]
A densidade volumétrica de cargas é dada por
\[ \bbox[#99CCFF,10px]
{\rho =\frac{Q}{V}}
\]
a carga total esta distribuída por uma esfera de volume igual a
\[ \bbox[#99CCFF,10px]
{V=\frac{4}{3}\pi R^{3}}
\]
então a densidade de cargas em função da carga total e do raio da distribuição pode ser escrita como
\[
\begin{gather}
\rho =\frac{Q}{\dfrac{4}{3}\pi R^{3}}\\[5pt]
\rho=\frac{3Q}{4\pi R^{3}} \tag{X}
\end{gather}
\]
substituindo a expressão (X) na expressão (IX)
\[
\begin{gather}
E=\frac{1}{\epsilon_{0}}\frac{\cancel{3}Q}{4\pi R^{3}}\frac{r}{\cancel{3}}\\[5pt]
E=\frac{Q}{4\pi \epsilon_{0}R^{3}}r \tag{XI}
\end{gather}
\]
- Para r > R:
Nesta situação a superfície Gaussiana passando pelo ponto onde se deseja calcular o campo elétrico
tem um raio rs = r externo à distribuição de cargas e o raio da distribuição de
cargas será o próprio raio da esfera rq = R (Figura 7).
Para o cálculo do campo elétrico é válida a mesma expressão obtida em (VIII).
Do lado esquerdo da igualdade os limites de integração serão os mesmos usados no caso anterior, apenas lembrando que agora o ponto r é externo à distribuição de cargas, de 0 a π em dθ e de 0 e 2π em dϕ, e temos rs = r, lembrando da Figura 3 acima.
Do lado direito os limites de integração serão de 0 a π em dθ, de 0 e 2π em dϕ e de 0 a R em drq.
Para o cálculo do campo elétrico é válida a mesma expressão obtida em (VIII).
Do lado esquerdo da igualdade os limites de integração serão os mesmos usados no caso anterior, apenas lembrando que agora o ponto r é externo à distribuição de cargas, de 0 a π em dθ e de 0 e 2π em dϕ, e temos rs = r, lembrando da Figura 3 acima.
Do lado direito os limites de integração serão de 0 a π em dθ, de 0 e 2π em dϕ e de 0 a R em drq.
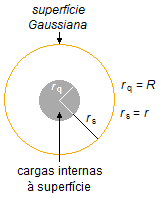
Figura 7
\[
Er^{2}\int_{0}^{\pi}\operatorname{sen}\theta \;d\theta \int_{0}^{{2\pi}}d\phi =\frac{\rho}{\epsilon_{0}}\int_{0}^{R}r_{q}^{2}\;dr_{q}\int_{0}^{\pi}\operatorname{sen}\theta \;d\theta \int_{0}^{{2\pi}}d\phi
\]
Integral de \( \displaystyle \int_{0}^{R}r_{q}^{2}\;dr_{q} \)
\[
\int_{0}^{R}r_{q}^{2}\;dr_{q}=\left.\frac{r_{q}^{\;2+1}}{2+1}\;\right|_{\;0}^{\;R}=\left.\frac{r_{q}^{\;3}}{3}\;\right|_{\;0}^{\;R}\;=\;\left(\;\frac{R^{\;3}}{3}-\frac{0^{3}}{3}\;\right)\;=\;\frac{R^{\;3}}{3}
\]
\[
\begin{gather}
Er^{2}\cancel{2}.\cancel{2}\cancel{\pi} =\frac{\rho}{\epsilon_{0}}\frac{R^{3}}{3}\cancel{2}.\cancel{2}\cancel{\pi}\\[5pt]
4\pi Er^{2}=4\pi \frac{\rho}{\epsilon_{0}}\frac{R^{3}}{3}\\[5pt]
E=\frac{\rho}{\epsilon_{0}r^{2}}\frac{R^{3}}{3} \tag{XII}
\end{gather}
\]
substituindo a expressão (X) na expressão (XII)
\[
\begin{gather}
E=\frac{1}{\epsilon_{0}r^{2}}\frac{\cancel{3}Q}{4\pi R^{3}}\frac{R^{3}}{\cancel{3}}\\[5pt]
E=\frac{Q}{4\pi \epsilon_{0}r^{2}} \tag{XIII}
\end{gather}
\]
Assim o campo elétrico em todo o espaço será dado pelas expressões (XI) e (XIII)
\[ \bbox[#FFCCCC,10px]
{
E=
\begin{cases}
\dfrac{Q}{4\pi \epsilon_{0}R^{3}}r &, & r\leqslant R\\
\dfrac{Q}{4\pi \epsilon_{0}r^{\;2}} &, & r\gt R
\end{cases}
}
\]
Observação: O campo elétrico em todo o espaço é dado por uma função definida por
partes.
Para \( r\;\leqslant \;R \) varia linearmente com a distância r como uma Equação do 1.º Grau \( y=ax+b \), onde \( \underbrace{E}_{y}=\underbrace{\frac{Q}{4\pi \epsilon_{0}R^{3}}}_{a}\underbrace{r}_{x}+\underbrace{0}_{b} \), como Q, π, &episilon;0 e R são constantes representam o coeficiente a, e como b = 0 na origem o campo elétrico é nulo \( \left(\text{para }r=0\text{, temos, }E=\frac{Q}{4\pi \epsilon_{0}R^{3}}.0\Rightarrow E=0\right) \text{.}\)
Para r > R o campo elétrico decai proporcionalmente a \( \frac{1}{r^{2}} \) como numa carga pontual.
Para \( r\;\leqslant \;R \) varia linearmente com a distância r como uma Equação do 1.º Grau \( y=ax+b \), onde \( \underbrace{E}_{y}=\underbrace{\frac{Q}{4\pi \epsilon_{0}R^{3}}}_{a}\underbrace{r}_{x}+\underbrace{0}_{b} \), como Q, π, &episilon;0 e R são constantes representam o coeficiente a, e como b = 0 na origem o campo elétrico é nulo \( \left(\text{para }r=0\text{, temos, }E=\frac{Q}{4\pi \epsilon_{0}R^{3}}.0\Rightarrow E=0\right) \text{.}\)
\[ \left(\text{para }r=0\text{, temos, }E=\frac{Q}{4\pi \epsilon_{0}R^{3}}.0\Rightarrow E=0\right) \]
O campo elétrico vai aumentando linearmente até que na superfície se comporta como se toda a carga Q
estivesse concentrada na origem e o campo fosse calculado a uma distância R
\( \left(\text{para }r=R\text{, temos, }E=\frac{Q}{4\pi \epsilon_{0}R^{3}}.R\Rightarrow E=\frac{Q}{4\pi \epsilon_{0}R^{2}}\right) \text{.}\)
\[ \left(\text{para }r=R\text{, temos, }E=\frac{Q}{4\pi \epsilon_{0}R^{3}}.R\Rightarrow E=\frac{Q}{4\pi \epsilon_{0}R^{2}}\right) \]
Para r > R o campo elétrico decai proporcionalmente a \( \frac{1}{r^{2}} \) como numa carga pontual.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .