Exercício Resolvido de Resolvido de Lei de Gauss
publicidade
Calcule o fluxo elétrico através de um hemisfério de raio a imerso num campo elétrico de intensidade
E.
Dados do problema:
- Raio do hemisfério: a;
- Intensidade do campo elétrico: E.
Solução:
O fluxo elétrico é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\Phi_{\small E}=\int_A{\mathbf E}\cdot d\mathbf A} \tag{I}
\end{gather}
\]
Adotamos um sistema de referência com o eixo-z na direção e sentido do vetor campo elétrico e os
eixos x e y na base do hemisfério, então o vetor campo elétrico pode ser escrito como
O vetor elemento de área é dado por
\[
\begin{gather}
\mathbf E=E\;\mathbf k \tag{II}
\end{gather}
\]
onde i, j e k são os vetores unitários nas direções x, y e z
respectivamente.O vetor elemento de área é dado por
\[
\begin{gather}
d\mathbf A=dA\;\mathbf n \tag{III}
\end{gather}
\]
onde n é o vetor unitário na direção perpendicular à superfície hemisférica.
Observação: A base ijk foi desenhada com o vetor na direção y no sentido para
baixo de modo que o sistema de eixos seja dextrogiro, ou seja obedeça à Regra da Mão Direita.
Substituindo as equações (II) e (III) na equação (I)
\[
\begin{gather}
\Phi_{\small E}=\int_AE\;\mathbf k\cdot dA\;\mathbf n \\[5pt]
\Phi_{\small E}=\int_AEdA\underbrace{\;\mathbf k\cdot\;\mathbf n}_{1}
\end{gather}
\]
Observação: Como k e n são vetores unitário seus módulos são iguais a 1 e o
ângulo entre eles é θ. O vetor k tem sua direção e sentido fixos no referencial, mas
o vetor n é normal à superfície hemisférica em cada ponto, variando de θ = 0, no ponto central
do hemisfério onde a direção e sentido de n e E coincidem, até
\( \theta=\frac{\pi}{2} \),
na borda da superfície onde n é perpendicular a E (Figura 2).
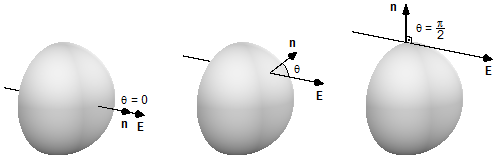Figura 2
O produto escalar entre eles será.
\[
\begin{gather}
\mathbf k\cdot\mathbf n=|\;\mathbf k\;|\;|\;\mathbf n\;|\cos\theta=1\times 1\times \cos\theta=\cos\theta
\end{gather}
\]
\[
\begin{gather}
\Phi_{\small E}=\int_AE\cos\theta\;dA \tag{IV}
\end{gather}
\]
Para visualizar o elemento de área dA giramos o hemisfério em torno do eixo-x (Figura 3).
O elemento de área dA será
\[
\begin{gather}
dA=r\;d\theta r\operatorname{sen}\theta\;d\phi\\
dA=r^2\operatorname{sen}\theta\;d\theta\;d\phi \tag{V}
\end{gather}
\]
substituindo a equação (V) na equação (IV)
\[
\begin{gather}
\Phi_{\small E}=\iint E\cos\theta r^2\operatorname{sen}\theta\;d\theta\;d\phi \\
\Phi_{\small E}=\iint Er^2\cos\theta\operatorname{sen}\theta\;d\theta\;d\phi
\end{gather}
\]
Como o campo elétrico é uniforme e a integral não depende do raio eles podem “sair” da integral e como não existem termos “cruzados” em θ e ϕ as integrais podem ser separadas
\[
\begin{gather}
\Phi_{\small E}=Er^2\int \cos\theta\operatorname{sen}\theta\;d\theta\int d\phi
\end{gather}
\]
Os limites de integração serão de 0 a
\( \frac{\pi}{2} \)
em dq e de 0 e 2π em d&varphoi; (uma volta completa na base do hemisfério)
\[
\begin{gather}
\Phi_{\small E}=Er^2\int_{0}^{{\frac{\pi}{2}}}\cos\theta\operatorname{sen}\theta\;d\theta\int_0^{2\pi}d\phi
\end{gather}
\]
Integral de
\( \displaystyle \int_0^{\frac{\pi}{2}}\cos\theta\operatorname{sen}\theta\;d\theta\)
fazendo a mudança de variável
para θ = 0
temos \( u=\operatorname{sen}0=0 \)
para \( \theta=\dfrac{\pi}{2} \)
temos \( u=\operatorname{sen}\dfrac{\pi}{2}=1 \)
fazendo a mudança de variável
\[
\begin{array}{l}
u=\operatorname{sen}\theta \\[5pt]
du=\cos\theta\;d\theta\Rightarrow d\theta=\dfrac{du}{\cos\theta}
\end{array}
\]
fazendo a mudança dos extremos de integração
para θ = 0
temos \( u=\operatorname{sen}0=0 \)
para \( \theta=\dfrac{\pi}{2} \)
temos \( u=\operatorname{sen}\dfrac{\pi}{2}=1 \)
\[
\begin{align}
\int_0^1\cancel{\cos\theta}\;u\;\frac{du}{\cancel{\cos\theta}} & \Rightarrow\int_0^1 u\;du\Rightarrow\left.\frac{u^{\;2}}{2}\;\right|_{\;0}^{\;1}\Rightarrow \\
& \Rightarrow\frac{1^{\;2}}{2}-\frac{0^{\;2}}{2}\;\Rightarrow\;\frac{1}{2}
\end{align}
\]
Integral de
\( \displaystyle \int_0^{2\pi}\;d\phi \)
\[
\begin{gather}
\int_0^{2\pi}\;d\phi=\left.\phi\;\right|_{\;0}^{\;2\pi}=2\pi-0=2\pi
\end{gather}
\]
\[
\begin{gather}
\Phi_{\small E}=Er^2\frac{1}{\cancel 2}\cancel 2\pi
\end{gather}
\]
para r = a
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Phi_{\small E}=\pi a^2E}
\end{gather}
\]
publicidade