Exercício Resolvido de Força Elétrica e Campo Elétrico
publicidade
Um disco de raio a está carregado com uma densidade de carga diretamente proporcional a posição
radial. Calcule o vetor campo elétrico em um ponto P sobre o eixo de simetria perpendicular ao
plano do disco a uma distância z do seu centro.

Dados do problema:
- Raio do disco: a;
- Distância ao ponto onde se quer o campo elétrico: z.
A densidade superficial de carga do disco é diretamente proporcional à posição radial da carga (Figura 1)
\[
\begin{gather}
\sigma (r)=\alpha r \tag{I}
\end{gather}
\]
onde α é uma constante que torna a expressão dimensionalmente consistente. Assim no centro do
disco onde o raio é nulo a densidade de carga é nula, na borda onde o raio é igual a a, a
densidade de carga vale αa.

Figura 1
O vetor posição r vai de um elemento de carga dq do disco até o ponto P onde se deseja calcular o campo elétrico, o vetor rq localiza o elemento de carga em relação à origem do referencial e o vetor rp localiza o ponto P (Figura 2-A).
\[
\mathbf{r}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\]
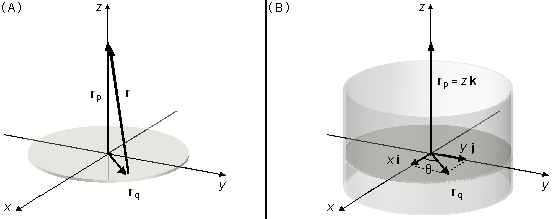
O vetor rq, que está no plano-xy, é escrito como \( {\mathbf{r}}_{q}=x\;\mathbf{i}+y\;\mathbf{j} \) e o vetor rp só possui componente na direção k, \( {\mathbf{r}}_{p}=z\;\mathbf{k} \), o vetor posição será (Figura 2-B)
\[
\begin{gather}
\mathbf{r}=z\;\mathbf{k}-\left(x\;\mathbf{i}+y\;\mathbf{j}\right)\\
\mathbf{r}=-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k} \tag{II}
\end{gather}
\]
Da expressão (II) o módulo do vetor posição r será
\[
\begin{gather}
r^{2}=x^{2}+y^{2}+z^{2}\\
r=\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}} \tag{III}
\end{gather}
\]
fazendo as seguintes definições para x, y e z (Figura 2-B)
\[
\left\{
\begin{array}{l}
x=r_{q}\cos \theta \\
y=r_{q}\operatorname{sen}\theta \\
z=z
\end{array}
\right. \tag{IV}
\]
Solução
O vetor campo elétrico é dado por
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{V}
\end{gather}
\]
Da expressão da densidade superficial de carga σ obtemos o elemento de carga dq
\[ \bbox[#99CCFF,10px]
{\sigma (r)=\frac{dq}{dA}}
\]
\[
\begin{gather}
dq=\sigma \;dA \tag{VI}
\end{gather}
\]
onde dA é um elemento de área.O elemento de área em coordenadas cartesianas é dado por
\[
dA=dx \;dy
\]
para obter o elemento de área em coordenadas polares calculamos o Jacobiano dado pelo determinante
\[
J=\left|
\begin{matrix}
\;\dfrac{\partial x}{\partial r}&\dfrac{\partial
x}{\partial \theta }\;\\
\;\dfrac{\partial y}{\partial r}&\dfrac{\partial
y}{\partial \theta }\;
\end{matrix}
\right|
\]
Cálculo das derivadas parciais das funções x e y dadas pelas expressões
em (IV)
\( x=r_{q}\cos \theta \):
\( \dfrac{\partial x}{\partial r_{q}}=\dfrac{\partial (r_{q}\cos \theta)}{\partial r_{q}}=\cos \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\cos \theta .1=\cos \theta \text{, } \)
\( \dfrac{\partial x}{\partial \theta }=\dfrac{\partial (r_{q}\cos \theta)}{\partial \theta }=r_{q}\dfrac{\partial (\cos \theta )}{\partial\theta }=r_{q}(-\operatorname{sen}\theta)=-r_{q}\operatorname{sen}\theta \text{, } \)
\( y=r_{q}\operatorname{sen}\theta \):
\( \dfrac{\partial y}{\partial r_{q}}=\dfrac{\partial(r_{q}\operatorname{sen}\theta )}{\partial r_{q}}=\operatorname{sen}\theta \dfrac{\partial r_{q}}{\partial r_{q}}=\operatorname{sen}\theta .1=\operatorname{sen}\theta \text{, } \)
\( \dfrac{\partial y}{\partial \theta }=\dfrac{\partial(r_{q}\operatorname{sen}\theta )}{\partial \theta }=r_{q}\dfrac{\partial(\operatorname{sen}\theta )}{\partial \theta }=r_{q}\cos \theta \text{, } \)
\( x=r_{q}\cos \theta \):
\( \dfrac{\partial x}{\partial r_{q}}=\dfrac{\partial (r_{q}\cos \theta)}{\partial r_{q}}=\cos \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\cos \theta .1=\cos \theta \text{, } \)
\[ \dfrac{\partial x}{\partial r_{q}}=\dfrac{\partial (r_{q}\cos \theta)}{\partial r_{q}}=\cos \theta \dfrac{\partial r_{q}}{\partial r_{q}}=\cos \theta .1=\cos \theta \]
na derivada em rq o valor de θ é constante e o cosseno sai da
derivada.
\( \dfrac{\partial x}{\partial \theta }=\dfrac{\partial (r_{q}\cos \theta)}{\partial \theta }=r_{q}\dfrac{\partial (\cos \theta )}{\partial\theta }=r_{q}(-\operatorname{sen}\theta)=-r_{q}\operatorname{sen}\theta \text{, } \)
\[ \dfrac{\partial x}{\partial \theta }=\dfrac{\partial (r_{q}\cos \theta)}{\partial \theta }=r_{q}\dfrac{\partial (\cos \theta )}{\partial\theta }=r_{q}(-\operatorname{sen}\theta)=-r_{q}\operatorname{sen}\theta \]
na derivada em θ o valor de rq é constante e sai da derivada.
\( y=r_{q}\operatorname{sen}\theta \):
\( \dfrac{\partial y}{\partial r_{q}}=\dfrac{\partial(r_{q}\operatorname{sen}\theta )}{\partial r_{q}}=\operatorname{sen}\theta \dfrac{\partial r_{q}}{\partial r_{q}}=\operatorname{sen}\theta .1=\operatorname{sen}\theta \text{, } \)
\[ \dfrac{\partial y}{\partial r_{q}}=\dfrac{\partial(r_{q}\operatorname{sen}\theta )}{\partial r_{q}}=\operatorname{sen}\theta \dfrac{\partial r_{q}}{\partial r_{q}}=\operatorname{sen}\theta .1=\operatorname{sen}\theta \]
na derivada em rq o valor de θ é constante e o seno sai da
derivada.
\( \dfrac{\partial y}{\partial \theta }=\dfrac{\partial(r_{q}\operatorname{sen}\theta )}{\partial \theta }=r_{q}\dfrac{\partial(\operatorname{sen}\theta )}{\partial \theta }=r_{q}\cos \theta \text{, } \)
\[ \dfrac{\partial y}{\partial \theta }=\dfrac{\partial(r_{q}\operatorname{sen}\theta )}{\partial \theta }=r_{q}\dfrac{\partial(\operatorname{sen}\theta )}{\partial \theta }=r_{q}\cos \theta \]
na derivada em θ o valor de rq é constante e sai da derivada.
\[
dA=dx\;dy=J\;dr_{q}\;d\theta
\]
\[
\begin{gather}
J=\left|
\begin{matrix}
\;\cos \theta
&-r_{q}\operatorname{sen}\theta \;\\
\;\operatorname{sen}\theta
&r_{q}\cos \theta
\end{matrix}
\right|\\[5pt]
J=\cos \theta r_{q}\cos \theta-(-r_{q}\operatorname{sen}\theta \operatorname{sen}\theta)\\[5pt]
J=r_{q}\cos ^{2}\theta +r_{q}\operatorname{sen}^{2}\theta\\[5pt]
J=r_{q}(\underbrace{\cos ^{2}\theta +\operatorname{sen}^{2}\theta}_{1})\\[5pt]
J=r_{q}
\end{gather}
\]
\[
\begin{gather}
dA=r_{q}\;dr_{q}\;d\theta \tag{VII}
\end{gather}
\]
substituindo as expressões (I) e (VII) na expressão (VI)
\[
\begin{gather}
dq=\alpha r_{q}^{2}\;dr_{q}\;d\theta \tag{VIII}
\end{gather}
\]
Substituindo as expressões (II), (III) e (VII) na expressão (V), e como a integração é feita sobre a superfície do
disco, depende de duas variáveis r e θ, temos uma integral dupla
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\alpha r_{q}^{2}\;dr_{q}\;d\theta}{\left[\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right)\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\alpha r_{q}^{2}\;dr_{q}\;d\theta}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}-y\;\mathbf{j}+z\;\mathbf{k}\right) \tag{IX}
\end{gather}
\]
substituindo as expressões (IV) na expressão (VIII)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\iint {\frac{\alpha r_{q}^{2}\;dr_{q}\;d\theta}{\left[\left(r_{q}\cos \theta\right)^{2}+\left(r_{q}\operatorname{sen}\theta\right)^{2}+z^{2}\right]^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\operatorname{sen}\theta\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\alpha r_{q}^{2}\;dr_{q}\;d\theta}{\left[r_{q}^{2}\cos ^{2}\theta +r_{q}^{2}\operatorname{sen}^{2}\theta+z^{2}\right]^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\operatorname{sen}\theta\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\alpha r_{q}^{2}\;dr_{q}\;d\theta}{\left[r_{q}^{2}\left(\underbrace{\cos ^{2}\theta+\operatorname{sen}^{2}\theta}_{1}\right)+z^{2}\right]^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\operatorname{sen}\theta\;\mathbf{j}+z\;\mathbf{k}\right)}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\iint {\frac{\alpha r_{q}^{2}\;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}\left(-r_{q}\cos \theta\;\mathbf{i}-r_{q}\operatorname{sen}\theta\;\mathbf{j}+z\;\mathbf{k}\right)}
\end{gather}
\]
A constante de proporcionalidade α pode “sair” da integral, e a integral da soma é igual a soma
das integrais
\[
\mathbf{E}=\frac{\alpha}{4\pi \epsilon_{0}}\left(-\iint {\frac{r_{q}^{3}\cos \theta \;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\;\mathbf{i}-\iint {\frac{r_{q}^{3}\;\operatorname{sen}\theta \;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\;\mathbf{j}+\iint {\frac{zr_{q}\;dr_{q}\;d\theta}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\mathbf{k}\right)
\]
Os limites de integração vão de 0 a a em drq, ao longo do raio do disco e de 0 e
2π em dθ, uma volta completa no disco, e as integrais podem ser separadas
\[
\begin{split}
\mathbf{E}=& \frac{\alpha}{4\pi \epsilon_{0}}\left(-\int_{0}^{a}{\frac{r_{q}^{3}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\underbrace{\int_{0}^{2\pi}{\cos \theta \;d\theta}}_{0}\;\mathbf{i}-\right.\\
& \left. -\int_{0}^{a}{\frac{r_{q}^{3}\;dr}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}}\underbrace{\int_{0}^{2\pi}{\operatorname{sen}\theta \;d\theta}}_{0}\;\mathbf{j}+z\int_{0}^{a}{\frac{r_{q}\;dr_{q} }{\left(r^{2}+z^{2}\right)^{\frac{3}{2}}}}\int_{0}^{2\pi}{d\theta}\;\mathbf{k}\right)
\end{split}
\]
Integração de \( \displaystyle \int_{0}^{2\pi}\cos \theta \;d\theta \)
1.º método
 Figura 3
Figura 3
1.º método
\[
\begin{split}
\int_{0}^{2\pi}\cos \theta \;d\theta &=\left.\operatorname{sen}\theta\;\right|_{\;0}^{\;2\pi }=\operatorname{sen}2\pi-\operatorname{sen}0=\\
&=0-0=0
\end{split}
\]
2.º método
O gráfico de cosseno entre 0 e 2π possui uma área “positiva” acima do eixo-x, entre 0 e \( \frac{\pi}{2} \) e entre \( \frac{3\pi}{2} \) e 2π, e uma área “negativa” abaixo do eixo-x, entre \( \frac{\pi}{2} \) e \( \frac{3\pi}{2} \), estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero (Figura 3).
O gráfico de cosseno entre 0 e 2π possui uma área “positiva” acima do eixo-x, entre 0 e \( \frac{\pi}{2} \) e entre \( \frac{3\pi}{2} \) e 2π, e uma área “negativa” abaixo do eixo-x, entre \( \frac{\pi}{2} \) e \( \frac{3\pi}{2} \), estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero (Figura 3).

Integração de \( \displaystyle \int_{0}^{2\pi}\operatorname{sen}\theta \;d\theta \)
1.º método
 Figura 4
Figura 4

Figura 5
1.º método
\[
\begin{split}
\int_{0}^{2\pi}\operatorname{sen}\theta \;d\theta &=\left.-\cos \theta\;\right|_{\;0}^{\;2\pi }=-(\cos 2\pi -\cos 0)=\\
&=-(1-1)=0
\end{split}
\]
2.º método
O gráfico do seno entre 0 e 2π possui uma área “positiva” acima do eixo-x, entre 0 e π, e uma área “negativa” abaixo do eixo-x, entre π e 2π, estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero. nas direções i e j (Figura 4).
O gráfico do seno entre 0 e 2π possui uma área “positiva” acima do eixo-x, entre 0 e π, e uma área “negativa” abaixo do eixo-x, entre π e 2π, estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero. nas direções i e j (Figura 4).

Observação: as duas integrais, nas direções i e j, que são nulas
representam o cálculo matemático para a afirmação que se faz usualmente de que as componentes do campo
elétrico paralelas ao plano-xy dEP se anulam. Apenas as
componentes normais ao plano dEN contribuem para o campo elétrico total
(Figura 5). Como as integrais em seno e cosseno são nulas não é preciso fazer a integral do raio .

Figura 5
Integração de \( \displaystyle \int_{{0}}^{a}{\frac{r_{q}\;dr_{q}}{\left(r_{q}^{2}+z^{2}\right)^{\frac{3}{2}}}} \)
fazendo a mudança de variável
para rq = 0
temos \( u=0^{2}+z^{2}\Rightarrow u=z^{2} \)
para rq = a
temos \( u=a^{2}+z^{2} \)
fazendo a mudança de variável
\[
\begin{array}{l}
u=r_{q}^{2}+z^{2}\\
\dfrac{du}{dr_{q}}=2r_{q}\Rightarrow dr_{q}=\dfrac{du}{2r_{q}}
\end{array}
\]
fazendo a mudança dos extremos de integração
para rq = 0
temos \( u=0^{2}+z^{2}\Rightarrow u=z^{2} \)
para rq = a
temos \( u=a^{2}+z^{2} \)
\[
\begin{split}
\int_{z^{2}}^{{a^{2}+z^{2}}}{\frac{r_{q}}{u^{\frac{3}{2}}}\;\frac{du}{2r_{q}}} &\Rightarrow\frac{1}{2}\int_{z^{2}}^{{a^{2}+z^{2}}}{\frac{1}{u^{\frac{3}{2}}}\;du}\Rightarrow\frac{1}{2}\left.\frac{u^{-{\frac{3}{2}+1}}}{-{\frac{3}{2}+1}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\\[5pt]
&\Rightarrow\frac{1}{2}\left.\frac{u^{\frac{-3+2}{2}}}{\frac{-{3+2}}{2}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\frac{1}{2}\left.\frac{u^{-{\frac{1}{2}}}}{-{\frac{1}{2}}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\\[5pt]
&\Rightarrow\left.-u^{-{\frac{1}{2}}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\left.-{\frac{1}{u^{\frac{1}{2}}}}\;\right|_{\;z^{2}}^{\;a^{2}+z^{2}}\Rightarrow\\[5pt]
&\Rightarrow-\left(\frac{1}{\sqrt{a^{2}+z^{2}}}-\frac{1}{\sqrt{z^{2}}}\right)\Rightarrow\frac{1}{z}-\frac{1}{\sqrt{a^{2}+z^{2}}}
\end{split}
\]
Integral de \( \displaystyle \int_{{0}}^{{2\pi}}\;d\theta \)
\[
\int_{{0}}^{{2\pi}}\;d\theta =\left.\theta \;\right|_{\;0}^{\;2\pi}=2\pi -0=2\pi
\]
\[
\begin{gather}
\mathbf{E}=\frac{\alpha}{4\pi \epsilon_{0}}\left[0\;\mathbf{i}-0\;\mathbf{j}+z\;\left(\frac{1}{z}-\frac{1}{\sqrt{a^{2}+z^{2}\;}}\right)2\pi\;\mathbf{k}\right]\\
\mathbf{E}=\frac{\alpha}{\cancelto{2}{4}\cancel{\pi} \epsilon_{0}}\left[\;\left(\frac{z}{z}-\frac{z}{\sqrt{a^{2}+z^{2}}}\right)\cancel{2}\cancel{\pi}\;\mathbf{k}\right]
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{{\mathbf{E}}=\frac{\alpha}{2\epsilon_{0}}\;\left(1-\frac{z}{\sqrt{\;a^{2}+z^{2}\;}}\right)\;{\mathbf{k}}}
\]

Figura 6
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .