Exercício Resolvido de Força Elétrica e Campo Elétrico
publicidade
Um pedaço de fio condutor é dobrado na forma de uma semicircunferência de raio a, este fio é carregado com uma carga elétrica Q distribuída uniformemente. No ponto P do centro da semicircunferência esta distribuição de cargas gera um campo elétrico de módulo E1.
Sendo o fio substituído por uma carga pontual de mesmo valor Q e a uma distância a, igual ao raio da semicircunferência, do ponto P ela gera neste ponto um campo elétrico de módulo E2.
Calcule a razão E1/E2, entre os módulos dos campos elétricos gerados pela semicircunferência carrega e pela carga pontual.

Dados do problema:
- Raio do arco: a;
- Carga do arco: Q;
- Carga pontual: Q.
O vetor posição r vai de um elemento de carga dq do arco até o ponto P onde se deseja calcular o campo elétrico, o vetor rq localiza o elemento de carga em relação à origem do referencial e o vetor rp localiza o ponto P, como neste caso o ponto P está na origem o vetor rp é nulo, rp = 0 (Figura 1-A)
\[
\mathbf{r}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\]
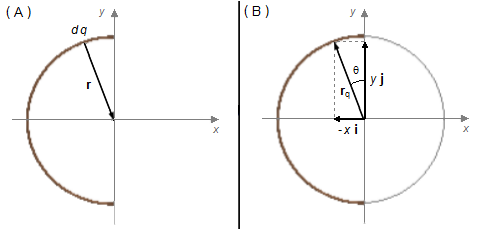
Pela geometria do problema devemos escolher coordenadas polares (Figura 1-B), o vetor rq, é escrito como \( {\mathbf{r}}_{q}=-x\;\mathbf{i}+y\;\mathbf{j} \), o vetor posição será
\[
\begin{gather}
\mathbf{r}=0-\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)\\
\mathbf{r}=x\;\mathbf{i}-y\;\mathbf{j} \tag{I}
\end{gather}
\]
Da expressão (I) o módulo do vetor posição r será
\[
\begin{gather}
r^{2}=x^{2}+y^{2}\\
r=\left(x^{2}+y^{2}\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
onde x e y, em coordenadas polares, são dados por
\[
\begin{gather}
x=a\operatorname{sen}\left(\theta-\frac{\pi}{2}\right)\\
x=a\left[\operatorname{sen}\theta \cos \frac{\pi}{2}-\operatorname{sen} \frac{\pi}{2} cos \theta \right]\\
x=a\left[\operatorname{sen}\theta .0-1. \cos \theta \right]\\
x=-a \cos \theta \tag{III-a}
\end{gather}
\]
\[
\begin{gather}
y=a\cos\left(\theta-\frac{\pi}{2}\right)\\
y=a \left[\cos \theta \cos \frac{\pi}{2}+\operatorname{sen} \theta \operatorname{sen}\frac{\pi}{2} \right]\\
y=a \left[\cos \theta .0+\operatorname{sen} \theta .1 \right]\\
y=a \operatorname{sen} \theta \tag{III-b}
\end{gather}
\]
Solução
O vetor campo elétrico do arco é dado por
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\]
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{IV}
\end{gather}
\]
Da expressão da densidade linear de carga λ obtemos o elemento de carga dq
\[ \bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\]
\[
\begin{gather}
q=\lambda \;ds \tag{V}
\end{gather}
\]
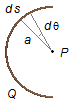
Figura 2
onde ds é um elemento de arco de ângulo dθ do aro (Figura 2)
\[
\begin{gather}
ds=a\;d\theta \tag{VI}
\end{gather}
\]
substituindo a expressão (VI) na expressão (V)
\[
\begin{gather}
dq=\lambda a\;d\theta \tag{VII}
\end{gather}
\]
Substituindo as expressões (I), (II) e (VII) na expressão (IV)
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi \epsilon_{0}}\int {\frac{\lambda a\;d\theta}{\left[\left(x^{2}+y^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)\\
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon _{0}}\int {\frac{\lambda a\;d\theta}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right) \tag{VIII}
\end{gather}
\]
substituindo as expressões (III-a) e (III-b) na expressão (VIII)
\[
\begin{gather}
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda a\;d\theta}{\left[\left(-a\cos \theta\right)^{2}+\left(a\operatorname{sen}\theta\right)^{2}\right]^{\frac{3}{2}}}\left(-a\cos \theta\;\mathbf{i}-a\operatorname{sen}\theta\;\mathbf{j}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda a\;d\theta}{\left[a^{2}\cos^{2}\theta +a^{2}\operatorname{sen}^{2}\theta\right]^{\frac{3}{2}}}\left(-a\cos \theta\;\mathbf{i}-a\operatorname{sen}\theta\;\mathbf{j}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda a\;d\theta}{\left[a^{2}\underbrace{\left(\cos ^{2}\theta +\operatorname{sen}^{2}\theta\right)}_{1}\right]^{\frac{3}{2}}}(-a)\left(\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{-\lambda a^{2}\;d\theta}{\left(a^{2}\right)^{\frac{3}{2}}}\left(\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{-\lambda a^{2}\;d\theta}{a^{3}}\left(\cos\theta \;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j}\right)}\\[5pt]
{\mathbf{E}}_{1}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{-\lambda \;d\theta }{a}\left(\cos \theta\;\mathbf{i}+\operatorname{sen}\theta\;\mathbf{j}\right)}
\end{gather}
\]
Como a densidade de carga λ e o raio a são constantes eles podem “sair” da integral, e sendo
a integral da soma igual à soma das integrais
\[
{\mathbf{E}}_{1}=-\frac{1}{4\pi \epsilon_{0}}\frac{\lambda}{a}\left(\int \cos \theta \;d\theta\;\mathbf{i}+\int \operatorname{sen}\theta \;d\theta\;\mathbf{j}\right)
\]
Os limites de integração serão
\( \dfrac{\pi}{2} \)
e
\( \dfrac{3\pi}{2} \)
(meia volta no círculo trigonométrico – Figura 3)
\[
{\mathbf{E}}_{1}=-\frac{1}{4\pi \epsilon_{0}}\frac{\lambda}{a}\left(\int _{{\frac{\pi }{2}}}^{{\frac{3\pi}{2}}}\cos \theta \;d\theta \;\mathbf{i}+\int_{{\frac{\pi}{2}}}^{{\frac{3\pi}{2}}}\operatorname{sen}\theta \;d\theta\;\mathbf{j}\;\right)
\]

Figura 3
Integral de \( \displaystyle \int_{{\frac{\pi}{2}}}^{{\frac{3\pi}{2}}}\cos \theta \;d\theta \)
\[
\begin{align}
\int_{{\frac{\pi}{2}}}^{{\frac{3\pi}{2}}}\cos \theta \;d\theta &=\left.\operatorname{sen}\theta \;\right|_{\;\frac{\pi}{2}}^{\;\frac{3\pi}{2}}=\operatorname{sen}\frac{3\pi}{2}-\operatorname{sen}\frac{\pi}{2}=\\
&=-1-1=-2
\end{align}
\]
Integral de \( \displaystyle \int _{{\frac{\pi}{2}}}^{{\frac{3\pi}{2}}}\operatorname{sen}\theta \;d\theta \)
\[
\begin{align}
\int _{{\frac{\pi}{2}}}^{{\frac{3\pi}{2}}}\operatorname{sen}\theta \;d\theta &=\left.-\cos \theta \;\right|_{\;\frac{\pi}{2}}^{\;\frac{3\pi}{2}}=-\left(\cos \frac{3\pi}{2}-\cos \frac{\pi}{2}\right)=\\
&=-(0-0)=0
\end{align}
\]
\[
\begin{gather}
{\mathbf{E}}_{1}=-\frac{1}{4\pi \epsilon_{0}}\frac{\lambda}{a}\left[-2\;\mathbf{i}+0\;\mathbf{j}\right]\\
{\mathbf{E}}_{1}=\frac{1}{2\pi \epsilon_{0}}\frac{\lambda}{a}\;\mathbf{i} \tag{IX}
\end{gather}
\]
A carga total do arco é Q, o comprimento de uma semicircunferência é metade do comprimento de uma
circunferência
\( C=\frac{2\pi a}{2}=\pi a \),
assim a densidade linear de carga pode ser escrita
\[
\begin{gather}
\lambda =\frac{Q}{\pi a} \tag{X}
\end{gather}
\]
substituindo a expressão (X) na expressão (IX)
\[
\begin{gather}
\mathbf{E}_{1}=\frac{1}{2\pi \epsilon_{0}}\frac{Q}{a\pi a}\;\mathbf{i}\\
\mathbf{E}_{1}=\frac{Q}{2\pi^{2}\epsilon _{0}a^{2}}\;\mathbf{i}
\end{gather}
\]
e o módulo do campo elétrico será
\[
\begin{gather}
E_{1}=\frac{Q}{2\pi ^{2}\epsilon_{0}a^{2}} \tag{XI}
\end{gather}
\]
O vetor campo elétrico gerado por uma carga pontual é dado por
\[
{\mathbf{E}}_{2}=\frac{1}{4\pi \epsilon_{0}}\frac{Q}{r^{2}}\frac{\mathbf{r}}{r}
\]
e seu módulo será
\[
E_{2}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{r^{2}}
\]
para uma distância r = a
\[
\begin{gather}
E_{2}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{a^{2}} \tag{XII}
\end{gather}
\]
A razão entre as intensidades dos campos elétricos gerados pela distribuição de cargas numa
semicircunferência e pela carga pontual é obtida dividindo-se a expressão (XI) pela expressão (XII)
\[
\begin{gather}
\frac{E_{1}}{E_{2}}=\frac{\dfrac{Q}{2\pi^{2}\epsilon_{0}a^{2}}}{\dfrac{1}{4\pi \epsilon_{0}}\dfrac{Q}{a^{2}}}\\[8pt]
\frac{E_{1}}{E_{2}}=\frac{\cancel{Q}}{\cancel{2}\pi ^{\cancel{2}}\cancel{\epsilon_{0}}\cancel{a^{2}}}\frac{\cancelto{2}{4}\cancel{\pi} \cancel{\epsilon_{0}}}{1}\frac{\cancel{a^{2}}}{\cancel{Q}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\frac{E_{1}}{E_{2}}=\frac{2}{\pi}}
\]
Observação: Este resultado significa que o campo gerado pela carga pontual é
\( E_{2}=\dfrac{\pi}{2}E_{1} \)
mais intenso (mais forte) que o campo gerado pela distribuição da mesma carga Q em uma
semicircunferência.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .